 |
9.3. Показатели надежности системы, состоящей из независимых элементов
|
|
|
|
9. 3. Показатели надежности системы, состоящей из независимых элементов
Всякая система характеризуется безотказностью и ремонтопригодностью. В качестве основной характеристики безотказности системы служит функция надежности, которая представляет собой вероятность безотказной работы в течение некоторого времени t.
Пусть система состоит из n элементов, функции надежности которых обозначим через p1(t), p2(t), …pn(t). Так как элементы, входящие в состав системы, являются независимыми, то вероятность безотказной работы системы определяется как произведение вероятностей составляющих ее элементов
Р(t) = p1(t)p2(t)... pn(t). (9. 6)
В частном случае, когда функции надежности составляющих элементов имеют экспоненциальное распределение с постоянными интенсивностями отказов, функция надежности системы определяется по формуле
n
P(t) = exp[-(λ 1 + λ 2 +…+ λ n)t] = exp[- Σ λ i t] (9. 7)
i = 1
Одной из важнейших характеристик безотказности системы является среднее время жизни, которое вычисляют, используя выражение
TC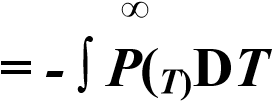 
. (9. 8)
0
Для случая экспоненциального распределения среднее время жизни системы равно
∞ n
Tc = ∫ exp[- Σ λ i t]dt = 1/(λ 1 + λ 2 +…+ λ n) (9. 9. )
0 i = 1
Среднее время жизни системы или наработку на отказ по результатам статистических данных вычисляют по формуле
|
|
|
Тc = T/m, (9. 10)
где T — суммарная наработка системы, полученная по результатам испытаний или эксплуатации; т — суммарное число отказов, зафиксированное в процессе испытаний или эксплуатации.
Коэффициент оперативной готовности характеризует надежность системы, необходимость применения которой возникает в произвольный момент времени (кроме планируемых периодов, в течение которых применение системы по назначению не предусматривается), начиная с которого система будет работать безотказно в течение заданного времени t. Значение коэффициента оперативной готовности определяют из выражения
Ко = Kг P(t) = Р(t) Tc/(Tc +Тв). (9. 11)
Пример 9. 2. Определить коэффициент оперативной готовности системы за период времени t = 10 ч, если известно, что система состоит из пяти элементов с соответствующими интенсивностями отказов, ч-1: λ 1 = 2. 10-5; λ 2 = 5. 10-5; λ 3 = 10-5; λ 4 = 20. 10-5; λ 5 = 50. 10-5, а среднее время восстановления при отказе одного элемента равно Tв = 10 ч. Результатами испытаний установлено, что распределение наработки на отказ подчиняется экспоненциальному закону.
Решение. Вероятность безотказной работы определим по формуле (9. 6): Р(t) = ехр[-Σ λ i t] ≈ l - (λ l+λ 2+λ з+λ 4+λ 5)10-5 t = =1- (2+5+1+20+50)10-5. 10 = 0, 992.
Значение Tc определяем по формуле (6. 37) Tc = 1/(λ 1 + λ 2 + λ 3 + λ 4 + λ 5) = 105/78 = 1282 ч.
Используя формулу (9. 10), вычислим коэффициент оперативной готовности
Ko = P(t)Tc/(Tc + Tв) = 0, 992. 1282/(1282 + 10) = 0, 984. Ответ: Ko = 0, 984.
Пример 9. 3. При эксплуатации в течении одного года (Tэ = 1 год = 8760 ч. ) изделий специального назначения было зафиксировано пять отказов (m = 5). На восстановление каждого отказа в среднем затрачено двадцать часов (Tв = 20 ч. ). За указанный период эксплуатации был проведен один регламент
|
|
|
(техническое обслуживание). Время регламента составило десять суток (Tр = 240 ч. ). Определить коэффициенты: готовности (Kг) и технического использования (Kи).
Решение. Коэффициент готовности определим по формуле Kг = 1 – (m Tв/Tэ ) = 1 – ( 5. 20/8760) = 0, 9886.
Коэффициент технического использования равен:
Kи = 1 – ( m Tв + Tр)/Tэ = 1 – (5. 20 + 240)/8760 = 0, 9612. Ответ: Kг= 0, 9886; Kи = 0, 9612.
Лекция 10 Расчет показателей надежности технических систем
10. 1. Структурные модели надежности сложных систем
Большинство технических систем являются сложными системами, состоящими из отдельных узлов, деталей, агрегатов, систем управления и т. п. Под сложной системой понимается объект, предназначенный для выполнения заданных функций, который может быть расчленен на элементы (компоненты), каждый из которых также выполняет определенные функции и находится во взаимодействии с другими элементами системы.
С позиций надежности сложная система обладает как отрицательными, так и положительными свойствами.
Факторы, отрицательно влияющие на надежность сложных систем:
- большое число элементов, отказ каждого из которых может привести к отказу всей системы;
- сложность оценки работоспособности сложных систем с точки зрения статистических данных в связи с их уникальностью и небольшим количеством;
- в связи с наличием у систем даже одинакового предназначения своих незначительных вариаций свойств отдельных элементов, которые сказываются на выходных параметрах системы. Чем сложнее система, тем большими индивидуальными особенностями она обладает.
Однако сложные системы обладают и такими свойствами, которые положительно влияют на их надежность:
- сложным системам свойственна самоорганизация, саморегулирование или самоприспособление, когда система способна найти наиболее устойчивое для своего функционирования состояние;
-для сложной системы часто возможно восстановление работоспособности по частям, без прекращения ее функционирования;
- не все элементы системы одинаково влияют на надежность сложной системы.
Анализ работоспособности сложной системы связан с изучением ее структуры и тех взаимосвязей, которые определяют ее надежное функционирование.
|
|
|
При анализе надежности сложные системы разбивают на элементы (компоненты) для того, чтобы вначале рассмотреть параметры и характеристики элементов, а затем оценить работоспособность всей системы. Под элементом можно понимать составную часть сложной системы, которая может характеризоваться самостоятельными входными и выходными параметрами. При исследовании надежности системы элемент не расчленяется на составные части, и показатели безотказности и долговечности относятся к элементу в целом. При этом возможно восстановление работоспособности элемента независимо от других частей и элементов системы.
Анализ надежности сложных систем имеет свои специфические особенности. Влияние различных отказов и снижение работоспособности элементов системы могут по-разному сказаться на надежности всей системы.
При анализе надежности сложной системы все ее элементы и компоненты целесообразно разделить на следующие группы.
- элементы, отказ которых практически не влияет на работоспособность системы (деформация ограждающего кожуха машины, изменение окраски поверхности и т. п. ). Отказы (т. е. неисправное состояние) этих элементов могут рассматриваться изолированно от системы.
- элементы, работоспособность которых за рассматриваемый период времени практически не изменяется (станины и корпусные детали, малонагруженные элементы с большим запасом прочности).
- элементы, ремонт или регулировка которых возможна при работе изделия или во время остановок, не влияющих на его эффективность
( подналадка и замена режущего инструмента на станке и т. д - элементы, отказ которых приводит к отказам системы.
Таким образом, рассмотрению и анализу надежности подлежат лишь элементы последней группы. Имеется ограниченное число элементов, которые в целом определяют надежность системы. Эти элементы и подсистемы выявляются при рассмотрении структурной схемы параметрической надежности.
|
|
|
