 |
Лекция №3. Дифференциальные уравнения переноса. Единый кинетический закон
|
|
|
|
Лекция №3
1. Дифференциальные уравнения переноса импульса, тепла, массы.
2. Общие принципы расчета процессов XT и БТ.
3. Лимитирующие стадии процессов.
Дифференциальные уравнения переноса
1. Уравнение переноса тепла (дифференциальное уравнение конвективного теплообмена Фурье – Кирхгофа).
Рассмотрим перенос тепла в однофазной, сплошной, изотропной среде без внутренних источников тепла γ =0 и с постоянными значениями параметров:
- а также отсутствует перенос тепла излучением
Потенциалом будет температура 
– плотность теплового потока.
Тогда основное уравнение для теплового потока примет вид (при условии неразрывности потока): 
Раскроем дивергенцию скалярного произведения и получим:
Т. к мы рассматриваем сплошную среду:
div w = 0
Проанализируем уравнение:
|
– локальная производная;
– конвективная;
(18)
Дифференциальное уравнение конвективного переноса теплоты или уравнение Фурье-Кирхгофа. ( 
– оператор Набла)
Описывает совокупность мгновенных значений параметра в каждой точке выделенного объема, т. е. описывает поле температур.
Частные случаи:
1. Процесс стационарный ( 
)
2. Однонаправленное движение вдоль оси Х
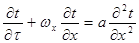
3. Перенос тепла в неподвижной среде (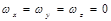 
)
|
|
|
4. Перенос тепла в неподвижной среде и процесс стационарный (нет перемещения макрообъемов)
, т. к. а 
0, то 
5. Одномерный стационарный перенос тепла в неподвижной среде:
2. Уравнение переноса вещества (дифференциальное уравнение конвективного массообмена Фика).
Рассмотрим перенос вещества в однофазной, сплошной, изотропной среде без внутренних источников вещества: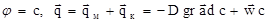 
Потенциалом переноса может быть плотность, тогда уравнение запишется:
Описывают поле концентраций в сплошном потоке однофазной изотропной среды.
Частные случаи:
1. Процесс стационарный ( 
)
2. Однонаправленное движение вдоль оси Х
3. Перенос вещества в неподвижной среде ( )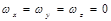
4. Перенос вещества в неподвижной среде и процесс стационарный
, т. к. D≠ 0, то 
5. Одномерный стационарный перенос теплоты в неподвижной среде: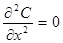 
3. Уравнение переноса импульса (дифференциальные уравнения Навье – Стокса).
Импульс 
векторная величина.
Рассмотрим перенос импульса в однофазной, сплошной, изотропной среде без внутренних источников импульса и с массовыми силами: давления, инерции, вязкости.
Ось х: 
| (1) | (2) | (3) | (4) |
Ось у: 
Ось z: 
x, y, z – проекции единичных массовых сил на соответствующие оси (массовые силы пропорциональны массе);
Единичная массовая сила – это массовая сила, отнесенная к единице массы объема, на который она действует, т. е. численно равна ускорению;
- кинематическая вязкость; влияние сил вязкости на перенос импульса;
ρ – плотность кг/м3;
Р – давление (Н/м2=Па);
w – средняя скорость движения.
Уравнение Навье-Стокса описывает поле скоростей в сплошном потоке однофазной изотропной среде. Каждое слагаемое учитывает силы: 1 – давление; 2 – массовые; 3 – инерции; 4 – вязкости (вязкостного трения).
|
|
|
Единый кинетический закон
Кинетика – наука о скорости и механизме процесса.
Скорость важнейшая характеристика т. к. она определяет основные размеры аппарата, а следовательно его материало- и энергоемкость, занимаемые или производственные площади. Чем скорость выше, тем размер аппарата меньше, материала меньше, производственные площади снижаются, т. е. затраты уменьшаются.
Скорость процесса пропорциональна градиенту соответствующего потенциала (движущей силе) и обратно пропорциональна сопротивлению переноса:
|
|
|
