1 Операции над многочленами
Многочленом (полиномом) степени k называется функция вида  , где x – переменная,
, где x – переменная, 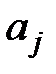 - числовые коэффициенты (j=0, …. k), и
- числовые коэффициенты (j=0, …. k), и  . Любое ненулевое число можно рассматривать как многочлен нулевой степени. Число 0 является единственным многочленом, степень которого не определена. Многочлены называются равными, в том случае, если равны их коэффициенты при одинаковых степенях. Коэффициенты многочлена обычно берутся из некоторого числового множества M. Множество всех многочленов с коэффициентами из M обозначают M(x). В качестве M обычно рассматривается числовое кольцо, либо числовое поле.
. Любое ненулевое число можно рассматривать как многочлен нулевой степени. Число 0 является единственным многочленом, степень которого не определена. Многочлены называются равными, в том случае, если равны их коэффициенты при одинаковых степенях. Коэффициенты многочлена обычно берутся из некоторого числового множества M. Множество всех многочленов с коэффициентами из M обозначают M(x). В качестве M обычно рассматривается числовое кольцо, либо числовое поле.
С многочленами над числовым кольцом можно проводить операции сложения, вычитания и умножения. Данные операции сводятся к приведению подобных членов. Ясно, что в результате получится многочлен с коэффициентами из этого же кольца. Выразим коэффициенты произведения многочленов через коэффициенты сомножителей. Пусть в результате перемножения многочленов 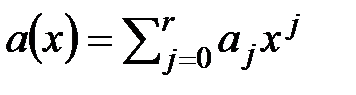 и
и 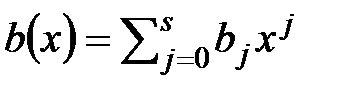 получается многочлен
получается многочлен  . Тогда
. Тогда 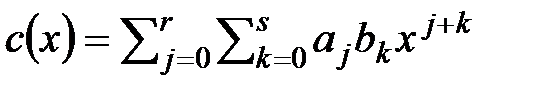 и после приведения подобных получим
и после приведения подобных получим 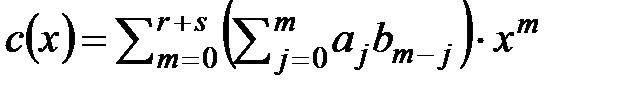 , в правой части равенства предполагается, что
, в правой части равенства предполагается, что  при
при  и
и  при j> s. Таким образом, найдены формулы для вычисления коэффициентов произведения
при j> s. Таким образом, найдены формулы для вычисления коэффициентов произведения 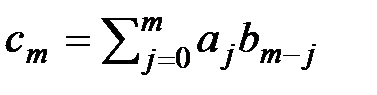 , где
, где  .
.
C многочленами над числовым полем, кроме перечисленных операций, определена операция деления с остатком. Задача деления многочлена 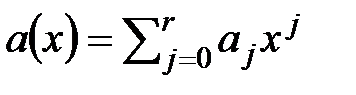 на многочлен
на многочлен 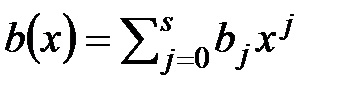 может быть сформулирована следующим образом: найти такой многочлен
может быть сформулирована следующим образом: найти такой многочлен  , называемый частным, при котором степень многочлена
, называемый частным, при котором степень многочлена 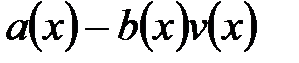 - наименьшая. Многочлен
- наименьшая. Многочлен 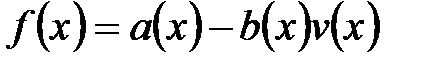 называется остатком деления
называется остатком деления 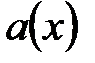 на
на 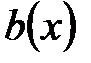 . Говорят, что многочлен a(x) делится на многочлен b(x), если остаток от деления равен нулю. Если степень
. Говорят, что многочлен a(x) делится на многочлен b(x), если остаток от деления равен нулю. Если степень  меньше степени
меньше степени 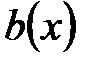 , то частное равно 0. Пусть степень
, то частное равно 0. Пусть степень  не меньше степени
не меньше степени 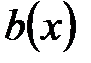 . Из требования минимальности степени
. Из требования минимальности степени 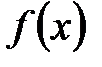 и правила умножения многочленов выводим, что степень
и правила умножения многочленов выводим, что степень 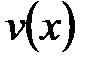 не превосходит r-s и
не превосходит r-s и 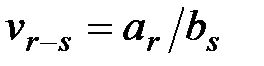 . Задача деления многочлена
. Задача деления многочлена  на многочлен
на многочлен 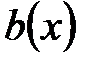 сводится к аналогичной задаче деления многочлена
сводится к аналогичной задаче деления многочлена 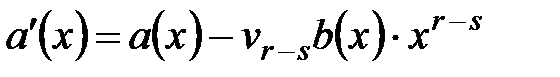 , но уже меньшей степени. Понятно, что таким образом частное и остаток от деления определяются единственным образом. Алгоритм деления оформляют
, но уже меньшей степени. Понятно, что таким образом частное и остаток от деления определяются единственным образом. Алгоритм деления оформляют
«
уголком » и чисто внешне похож на деление целых чисел с остатком. В качестве примера, деление «уголком» многочлена
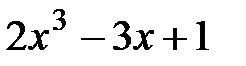
на многочлен
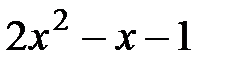
с остатком приведено на рисунке слева.
При делении на двучлен
x-a можно воспользоваться более компактной схемой деления, называемой
схемой Горнера. В основе этой схемы лежит очевидный факт, что при выполнении деления «уголком» на каждом шаге меняется только один коэффициент в текущем «остатке». Поэтому, схему деления «уголком» можно записать в одну строчку. Для примера, поделим многочлен

на двучлен

по схеме Горнера. Результат приведен на рисунке слева.
Кроме перечисленных операций используется операция подстановки в многочлен, или вычисления значения многочлена в точке. При выполнении данной операции, вместо переменной подставляют число. В результате получается числовое выражение, значение которого и называется значением многочлена. Число, значение многочлена в котором равно 0, называется корнем многочлена. Теорема Безе утверждает, что остаток от деления многочлена f(x) на двучлен x-a равен f(a). Таким образом, схему Горнера можно использовать не только для вычисления частного и остатка от деления на двучлен, но и для вычисления значения многочлена в точке.
Воспользуйтесь поиском по сайту:


 , где x – переменная,
, где x – переменная, 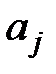 - числовые коэффициенты (j=0, …. k), и
- числовые коэффициенты (j=0, …. k), и  . Любое ненулевое число можно рассматривать как многочлен нулевой степени. Число 0 является единственным многочленом, степень которого не определена. Многочлены называются равными, в том случае, если равны их коэффициенты при одинаковых степенях. Коэффициенты многочлена обычно берутся из некоторого числового множества M. Множество всех многочленов с коэффициентами из M обозначают M(x). В качестве M обычно рассматривается числовое кольцо, либо числовое поле.
. Любое ненулевое число можно рассматривать как многочлен нулевой степени. Число 0 является единственным многочленом, степень которого не определена. Многочлены называются равными, в том случае, если равны их коэффициенты при одинаковых степенях. Коэффициенты многочлена обычно берутся из некоторого числового множества M. Множество всех многочленов с коэффициентами из M обозначают M(x). В качестве M обычно рассматривается числовое кольцо, либо числовое поле. 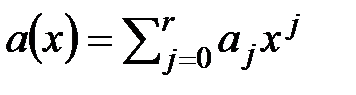 и
и 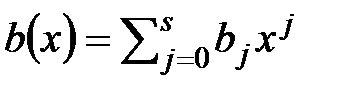 получается многочлен
получается многочлен  . Тогда
. Тогда 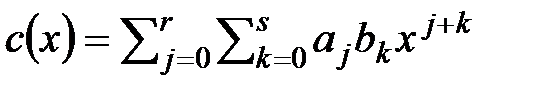 и после приведения подобных получим
и после приведения подобных получим 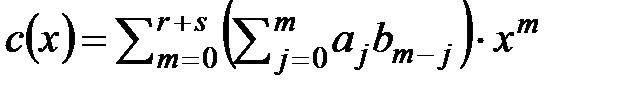 , в правой части равенства предполагается, что
, в правой части равенства предполагается, что  при
при  и
и  при j> s. Таким образом, найдены формулы для вычисления коэффициентов произведения
при j> s. Таким образом, найдены формулы для вычисления коэффициентов произведения 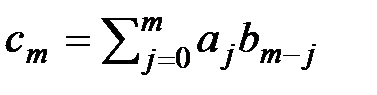 , где
, где  .
. 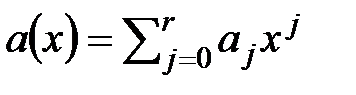 на многочлен
на многочлен 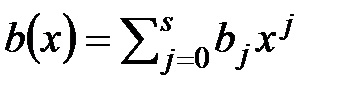 может быть сформулирована следующим образом: найти такой многочлен
может быть сформулирована следующим образом: найти такой многочлен  , называемый частным, при котором степень многочлена
, называемый частным, при котором степень многочлена 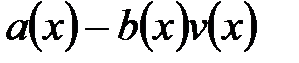 - наименьшая. Многочлен
- наименьшая. Многочлен 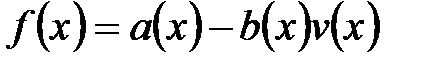 называется остатком деления
называется остатком деления 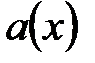 на
на 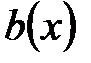 . Говорят, что многочлен a(x) делится на многочлен b(x), если остаток от деления равен нулю. Если степень
. Говорят, что многочлен a(x) делится на многочлен b(x), если остаток от деления равен нулю. Если степень  меньше степени
меньше степени 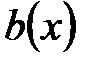 , то частное равно 0. Пусть степень
, то частное равно 0. Пусть степень  не меньше степени
не меньше степени 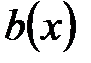 . Из требования минимальности степени
. Из требования минимальности степени 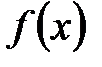 и правила умножения многочленов выводим, что степень
и правила умножения многочленов выводим, что степень 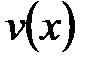 не превосходит r-s и
не превосходит r-s и 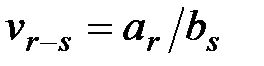 . Задача деления многочлена
. Задача деления многочлена  на многочлен
на многочлен 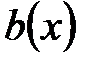 сводится к аналогичной задаче деления многочлена
сводится к аналогичной задаче деления многочлена 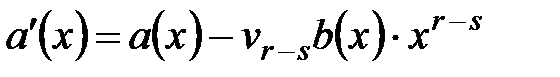 , но уже меньшей степени. Понятно, что таким образом частное и остаток от деления определяются единственным образом. Алгоритм деления оформляют
, но уже меньшей степени. Понятно, что таким образом частное и остаток от деления определяются единственным образом. Алгоритм деления оформляют 






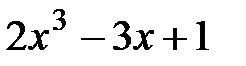 на многочлен
на многочлен 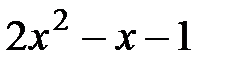 с остатком приведено на рисунке слева.
с остатком приведено на рисунке слева. 
 на двучлен
на двучлен  по схеме Горнера. Результат приведен на рисунке слева.
по схеме Горнера. Результат приведен на рисунке слева.


