 |
5 Разложение многочлена над полем рациональных чисел
|
|
|
|
4. 1 Упражнение
1. Доказать свойство неприводимых многочленов
1. A
2. B
3. C
4. D
2. Является ли многочлен неприводимым над полем Q, R, C.
1. 
2. 
3. 
4. 
5. 
6. 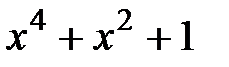
3. Разложить в произведение линейных множителей над C
1. 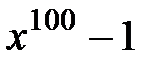
2. 
3. 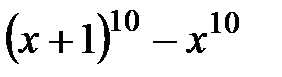
4. 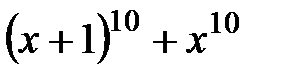
5. 
6. 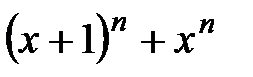
5 Разложение многочлена над полем рациональных чисел
Многочлен над кольцом целых чисел называется примитивным, если наибольший общий делитель его коэффициентов равен 1. Многочлен с рациональными коэффициентами единственным образом представляется в виде произведения положительного рационального числа, называемого содержанием многочлена, и примитивного многочлена. Произведение примитивных многочленов есть примитивный многочлен. Из данного факта вытекает, что если многочлен с целочисленными коэффициентами приводим над полем рациональных чисел, то он приводим над кольцом целых чисел. Таким образом, задача разложения многочлена на неприводимые множители над полем рациональных чисел сводится к аналогичной задаче над кольцом целых чисел.
Пусть  - многочлен с целыми коэффициентами и содержанием 1, а
- многочлен с целыми коэффициентами и содержанием 1, а  - его рациональный корень. Представим корень многочлена в виде несократимой дроби
- его рациональный корень. Представим корень многочлена в виде несократимой дроби  . Многочлен f(x) представляется в виде произведения примитивных многочленов
. Многочлен f(x) представляется в виде произведения примитивных многочленов  . Следовательно,
. Следовательно,
A. числитель  является делителем
является делителем  ,
,
B. знаменатель 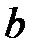 – делителем
– делителем 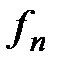
C. для любого целого k значение f(k) – целое число, которое делится без остатка на (bk-a).
Перечисленные свойства позволяют свести задачу отыскания рациональных корней многочлена к конечному перебору. Похожий подход используется в разложении многочлена f на неприводимые множители над полем рациональных чисел методом Кронекера. Если многочлен f(x) степени n приводим, то один из множителей имеет степень не выше n/2. Обозначим этот множитель через g(x). Поскольку все коэффициенты многочленов суть целые числа, то для любого целого a значение f(a) делится без остатка на g(a). Выберем m=1+n/2 различных целых чисел ai, i=1, …, m. Для чисел g(ai) существует конечное число возможностей (число делителей любого ненулевого числа конечно), следовательно, существует конечное число многочленов, которые могут быть делителями f(x). Осуществив полный перебор, либо покажем неприводимость многочлена, либо разложим его в произведение двух многочленов. К каждому множителю применим указанную схему до тех пор, пока все множители не станут неприводимыми многочленами.
|
|
|
Неприводимость некоторых многочленов над полем рациональных чисел можно установить с помощью простого критерия Эйзенштейна.
Пусть f(x) многочлен над кольцом целых чисел. Если существует простое число p, что
I. Все коэффициенты многочлена f(x), кроме коэффициента при старшей степени, делятся на p
II. Коэффициент при старшей степени не делится на p
III. Свободный член не делится на 
Тогда многочлен f(x) неприводим над полем рациональных чисел.
Следует отметить, что критерий Эйзенштейна даёт достаточные условия неприводимости многочленов, но не необходимые. Так многочлен  является неприводимым над полем рациональных чисел, но не удовлетворяет критерию Эйзенштейна.
является неприводимым над полем рациональных чисел, но не удовлетворяет критерию Эйзенштейна.
Многочлен  , по критерию Эйзенштейна, является неприводимым. Следовательно, над полем рациональных чисел найдётся неприводимый многочлен степени n, где n любое натуральное число больше 1.
, по критерию Эйзенштейна, является неприводимым. Следовательно, над полем рациональных чисел найдётся неприводимый многочлен степени n, где n любое натуральное число больше 1.
|
|
|


