 |
7.1 Упражнения. 8 Основная теорема Алгебры, и ее следствия. 9 Вещественные корни, теорема Штурма
|
|
|
|
7. 1 Упражнения
1. Выразить через элементарные симметрические многочлены
1. 
2. 
3. 
4. 
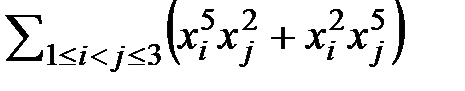
5. 
6. 
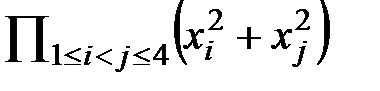
7. 
8. 
9.
2. Выразить через элементарные симметрические многочлены
1. 
2. 
3. 
4. 
5. 
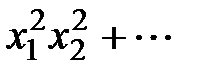
6. 
7. 
8. 
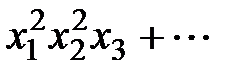
9. 
10. 
11. 
12. 
3. Вычислить значение симметрической функции от корней многочлена f(x)
1. , 
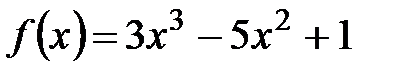
2. , 
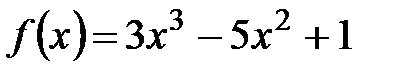
3. , 
4. , 
5. , 
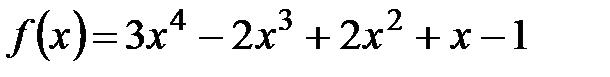
6. ,
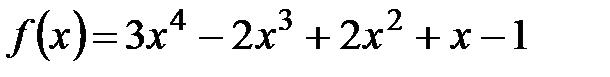
7. ,
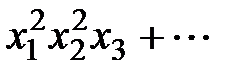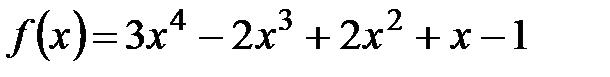
8. ,
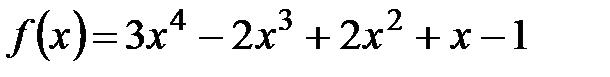
4. Корни многочлена 
обозначим через 
. Найти многочлен, корни которого являются
1. 
, 
, 
2. 
, 
, 
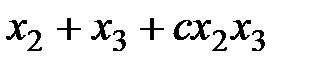
3. 
, 
, 
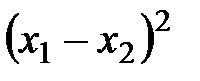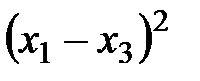4. 
, 
, 
5. 
, 
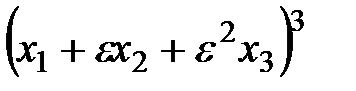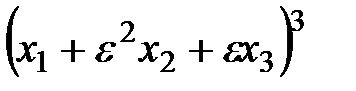, где 
5. Написать многочлен, корнями которого являются квадраты корней многочлена
1. 
2. 
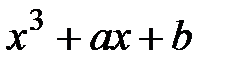
3. 
4. 
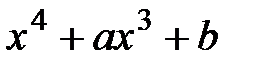
5. 
6. 
6. Многочлен 
имеет корни 
. Какие корни имеют многочлены:
1. 
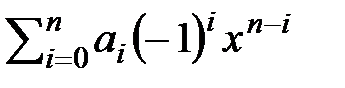
2. 
3. 
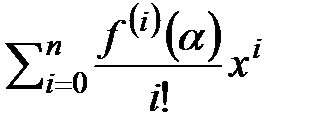
4. 
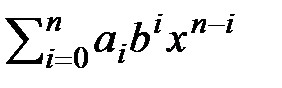
7. Определить 
так, чтобы
1. один из корней многочлена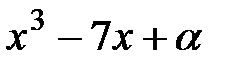 
равнялся удвоенному другому
2. сумма двух корней многочлена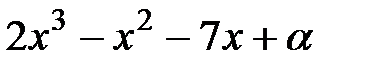 
равна 1
8 Основная теорема Алгебры, и ее следствия
Основная теорема алгебры утверждает, что любой многочлен над полем комплексных чисел имеет хотя бы один комплексный корень. Следовательно, многочлен над полем комплексных чисел разлагается в произведение линейных множителей. Разложение единственно с точностью до перестановки сомножителей. Рассмотрим многочлен с вещественными коэффициентами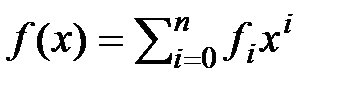 
. Над полем комплексных чисел он раскладывается на линейные множители. Если a его комплексный корень, то 
, т. е.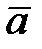 
то же корень f(x). Таким образом, многочлен f(x) делится на трёхчлен 
с вещественными коэффициентами. Следовательно, над полем вещественных чисел многочлен раскладывается в произведение неприводимых многочленов степени 1 и 2. Разложение единственно с точностью до перестановки сомножителей.
8. 1 Упражнения
1. Разложить многочлен на неприводимые множители над полем комплексных чисел
1. 
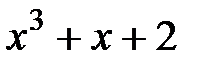
2. 
3. 
4. 
|
|
|
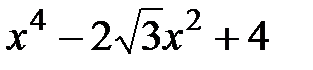
5. 
6. 
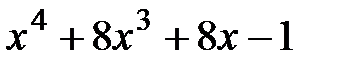
7. 
8. 
9. 
10. 
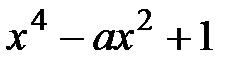, где 
11. 
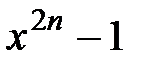
12. 
2. Разложить на неприводимые множители над полем вещественных чисел
1. 
2. 
3. 
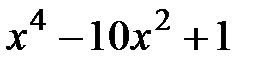
4. 
5. 
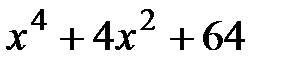
6. 
7. 
8. 
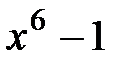
9. 
10. 
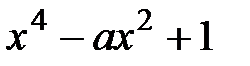, где 
11. 
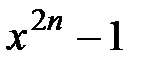
12. 
3. По заданным корням построить многочлен наименьшей степени а) с рациональными коэффициентами, б) с вещественными коэффициентами, в)с комплексными коэффициентами
1. 
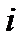- корень кратности 2, простые корни 1, 2, 3
2. 1 – корень кратности 2, простые корни 1-2i, 2, 3
3. корни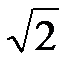 
, 
, 1
4. 
- кратности, простые корни 2, 
5. 
- кратности 2, простые корни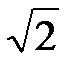 
, 
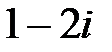
9 Вещественные корни, теорема Штурма
Последовательность многочленов 
назовём последовательностью многочленов Штурма, если она удовлетворяет следующим условиям:
I. Любые два соседних многочлена не имеют общих корней
II. Если a – корень 
при i> 0, то 
III. Последний многочлен не имеет вещественных корней.
IV. Если в окрестностях корня a многочлена 
сам многочлен возрастает, то 
, а если убывает, то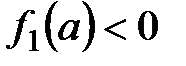 
Для последовательности многочленов F и числа a определим w(a) – число перемен знака в числовой последовательности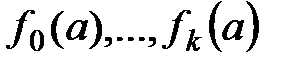 
(нули игнорируем). Число различных корней многочлена 
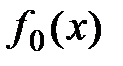на отрезке 
равно 
.
Пусть многочлен f(x) не имеет кратных корней. Построим последовательность многочленов: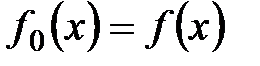 
, 
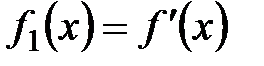, и далее, 
- остаток от деления 
на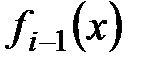 
умноженный на -1.
Данная последовательность многочленов будет последовательностью многочленов Штурма. Действительно, условие IV выполнено по свойству производной. Наибольший общий делитель многочлена и его производной равен 1, т. к. нет кратных корней. Таким образом, последний многочлен в ряду равен константе и не имеет вещественных корней. Из равенства 
вытекает условие II. Подставив x=a, где a – корень 
, получим 
. Общего корня у соседних многочленов не может быть, так как его наличие приводит к существованию кратных корней у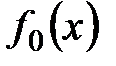 
.
9. 1 Упражнения
1. Отделить вещественные корни многочлена
1. 
2. 
3. 
4. 
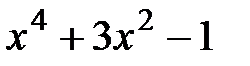
5. 
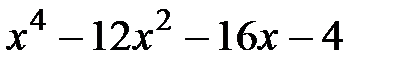
6. 
7. 
8. 
9. 
10. 
11. 
12. 
|
|
|
13. 
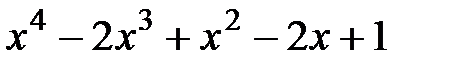
14. 
15. 
16. 
2. Определить число вещественных корней многочленов
1. 
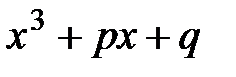
2. 
3. 
4. 
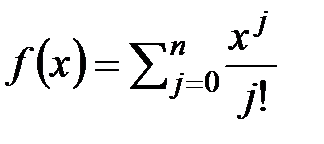
5. 
6. 
|
|
|
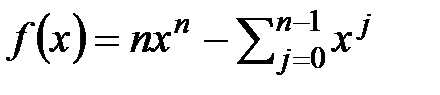
