 |
1.1 Упражнения. 2 Наименьшее общее кратное, наибольший общий делитель. Алгоритм Евклида
|
|
|
|
1. 1 Упражнения
1. Найти коэффициенты многочлена
1. 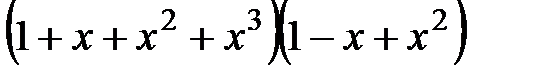
2. 
3. 
4. 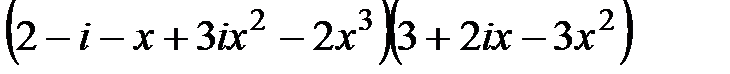
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 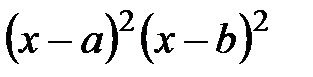
13. 
14. 
15. 
16. 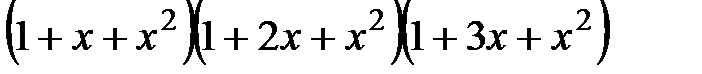
17. 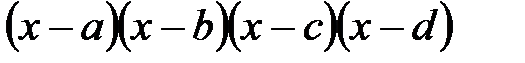
18. 
19. 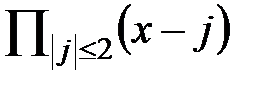
20. 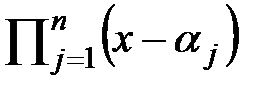
2. Найти частное и остаток от деления  на
на 
1.  ,
, 
2.  ,
, 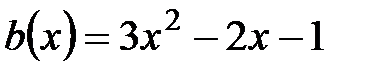
3.  ,
, 
4.  ,
, 
5.  ,
, 
6.  ,
, 
7.  ,
, 
8.  ,
, 
9.  ,
, 
10. 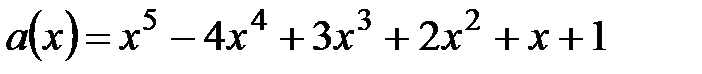 ,
, 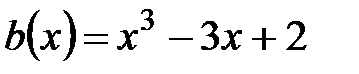
11. 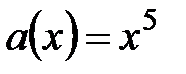 ,
, 
12. 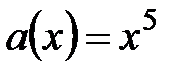 ,
, 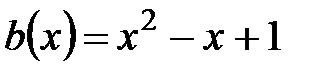
13. 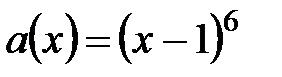 ,
, 
14.  ,
, 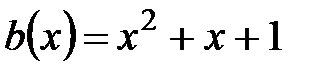
15. 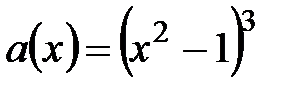 ,
, 
16. 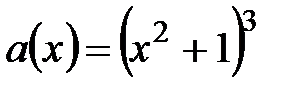 ,
, 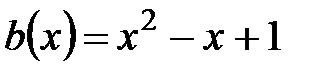
17.  ,
, 
18.  ,
, 
19. 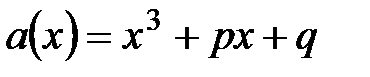 ,
, 
20. 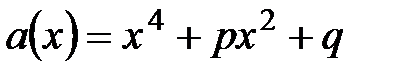 ,
, 
3. Поделить с помощью схемы Горнера  на двучлен
на двучлен 
1.  ,
, 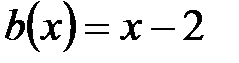
2.  ,
, 
3.  ,
, 
4. 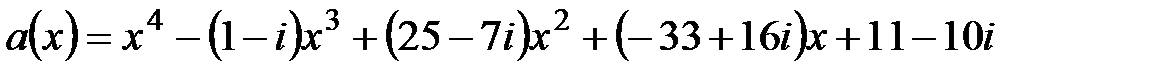 ,
, 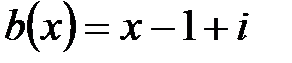
5.  ,
, 
4. С помощью схемы Горнера разложить 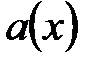 по степеням
по степеням 
1.  ,
, 
2.  ,
, 
3.  ,
, 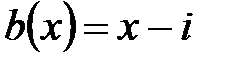
4. 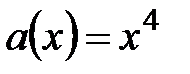 ,
, 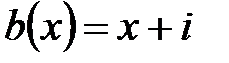
5. 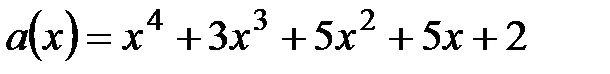 ,
, 
6. 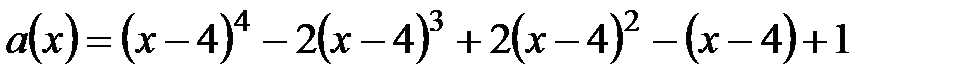 ,
, 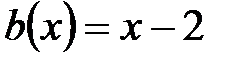
7.  ,
, 
8.  ,
, 
9.  ,
, 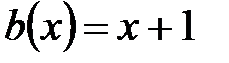
10.  ,
, 
11.  ,
, 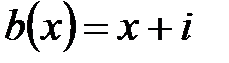
12.  ,
, 
13.  ,
, 
14.  ,
, 
15. 
 ,
, 
5. Найти остаток от деления 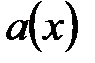 на
на 
1.  ,
, 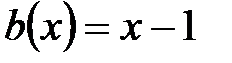
2.  ,
, 
3.  ,
, 
4.  ,
, 
5. 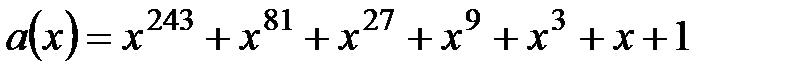 ,
, 
6. При каких условиях 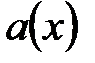 делится на
делится на 
1. 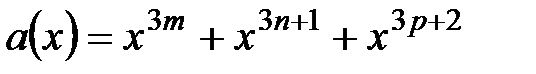 ,
, 
2.  ,
, 
3. 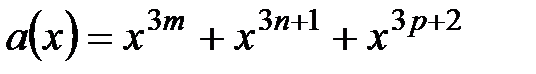 ,
, 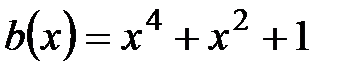
4. 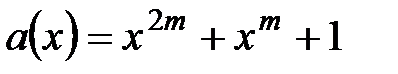 ,
, 
5. 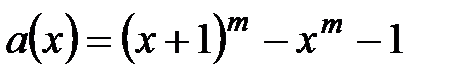 ,
, 
6. 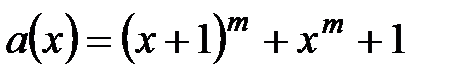 ,
, 
7.  ,
, 
7. Найти сумму коэффициентов многочлена
1. 
2. 
8. Найти многочлен наименьшей степени, корнями которого являются
1.  ,
,  ,
,  ,
, 
2. 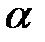 ,
, 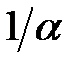 ,
,  ,
,  ,
, 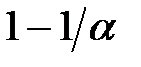 ,
, 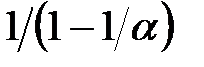
2 Наименьшее общее кратное, наибольший общий делитель. Алгоритм Евклида
Многочлен наименьшей степени, делящийся на f(x) и g(x) называется их наименьшим общим кратным и обозначается НОК(f(x), g(x)). Наименьшее общее кратное многочленов определено с точностью до числового множителя. Для пары многочленов f(x) и g(x) под общим делителем будем понимать многочлен, который делит f(x) и g(x) без остатка. Общий делитель определён с точностью до числового множителя. Общий делитель пары многочленов f(x) и g(x) наибольшей степени называется наибольшим общим делителем, и обозначается НОД(f(x), g(x)). Наибольший общий делитель многочленов является наименьшим общим кратным их общих делителей. Если наибольший общий делитель многочленов равен 1, то они называются взаимно простыми. Приведем простейшие свойства НОД и НОК многочленов.
A. Если многочлен h(x) делится на многочлены f(x) и g(x), то h(x) делится на НОК(f(x), g(x)).
B. 
C. Если v(x) взаимно просто с g(x), то 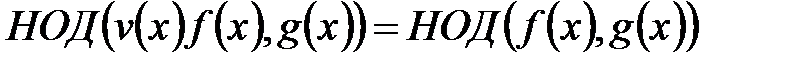
D. Для любого v(x) справедливо равенство 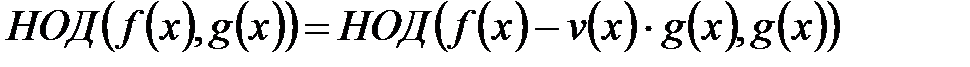 .
.
|
|
|
Видно, что свойства НОД и НОК многочленов похожи на свойства НОД и НОК целых чисел. В курсе «абстрактная алгебра» будет показано, что эта аналогия не случайна. Воспользуемся данной похожестью для демонстрации алгоритма Евклида построения наибольшего общего делителя. В основе алгоритма Евклида лежит свойство D, которое для чисел выглядит следующим образом. Для любых целых чисел v, f, g справедливо равенство 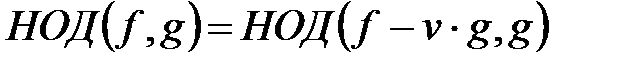 . Если в качестве v выбирать частное от деления f на g, то, в конечном счете, получим цепочку равенств, заканчивающейся парой чисел, в которой одно из них равно нулю. Для такой пары, наибольший общий делитель равен ненулевому числу. Для примера, найдем алгоритмом Евклида НОД(14, 48). Справедливы равенства НОД(14, 48)=НОД(14, 48-3 14)=НОД(14, 6)=НОД(14-2 6, 6)= =НОД(2, 6)=НОД(2, 6-3 2)=НОД(2, 0)=2.
. Если в качестве v выбирать частное от деления f на g, то, в конечном счете, получим цепочку равенств, заканчивающейся парой чисел, в которой одно из них равно нулю. Для такой пары, наибольший общий делитель равен ненулевому числу. Для примера, найдем алгоритмом Евклида НОД(14, 48). Справедливы равенства НОД(14, 48)=НОД(14, 48-3 14)=НОД(14, 6)=НОД(14-2 6, 6)= =НОД(2, 6)=НОД(2, 6-3 2)=НОД(2, 0)=2.
Аналогичным образом ищется наибольший общий делитель многочленов. Для примера, построим наибольший общий делитель многочленов  и
и  алгоритмом Евклида. Из равенства
алгоритмом Евклида. Из равенства 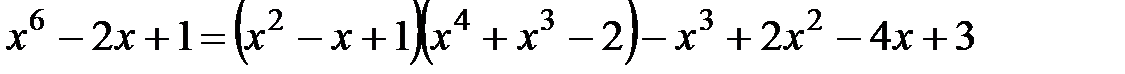 выводим
выводим  . Далее, из равенства
. Далее, из равенства  получаем
получаем  , из
, из 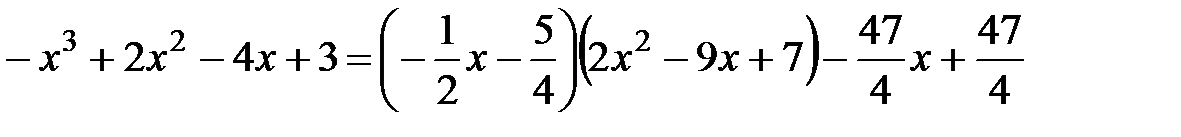 находим
находим  . Так как НОД многочленов не изменится, если один из них умножить на число
. Так как НОД многочленов не изменится, если один из них умножить на число  , то
, то  . Многочлен
. Многочлен  делится без остатка на x-1, поэтому
делится без остатка на x-1, поэтому  . Таким образом, наибольший общий делитель многочленов
. Таким образом, наибольший общий делитель многочленов 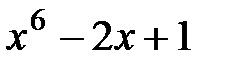 и
и  равен x-1.
равен x-1.
Кроме наибольшего общего делителя целых чисел a и b (многочленов) часто требуется найти его представление через исходные числа (многочлены), то есть представление вида ua+wb=НОД(a, b), где u и w- целые числа (многочлены).
Для нахождения целых чисел u и w воспользуемся расширенным алгоритмом Евклида. Для этого запишем систему уравнений 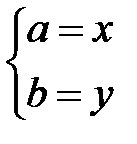 и применим к левым частям ее строк алгоритм Евклида. В результате получим уравнение НОД(a, b)=ux+wy. Подставив вместо x и y числа a и b, получим требуемое представление. При организации вычислительного процесса пишутся только коэффициенты при переменных x и y. В качестве примера применим расширенный алгоритм Евклида к паре чисел 14 и 48. Коэффициенты уравнений будем записывать в столбцах. Начиная с таблицы
и применим к левым частям ее строк алгоритм Евклида. В результате получим уравнение НОД(a, b)=ux+wy. Подставив вместо x и y числа a и b, получим требуемое представление. При организации вычислительного процесса пишутся только коэффициенты при переменных x и y. В качестве примера применим расширенный алгоритм Евклида к паре чисел 14 и 48. Коэффициенты уравнений будем записывать в столбцах. Начиная с таблицы  , путем операций со столбцами, указанными в скобках,
, путем операций со столбцами, указанными в скобках, 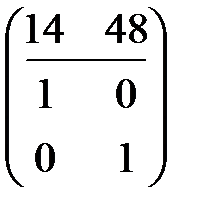 ([2]-3[1]),
([2]-3[1]), 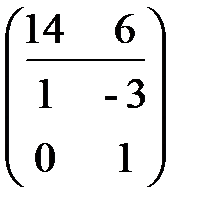 ([1]-2[2]),
([1]-2[2]), 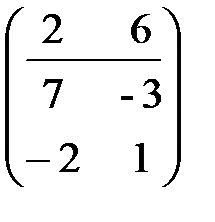 ([2]-3[1]),
([2]-3[1]), 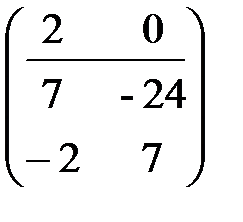 получим равенство 2=7 14-2 48. Последнюю таблицу можно не вычислять, поскольку все необходимые данные есть в предыдущей таблице.
получим равенство 2=7 14-2 48. Последнюю таблицу можно не вычислять, поскольку все необходимые данные есть в предыдущей таблице.
|
|
|
Аналогичный процесс можно провести и с многочленами. Применим расширенный алгоритм Евклида к многочленам  и
и  . Начиная с таблицы
. Начиная с таблицы  , путем операций со столбцами,
, путем операций со столбцами,  ([1]-
([1]-  [2]),
[2]), 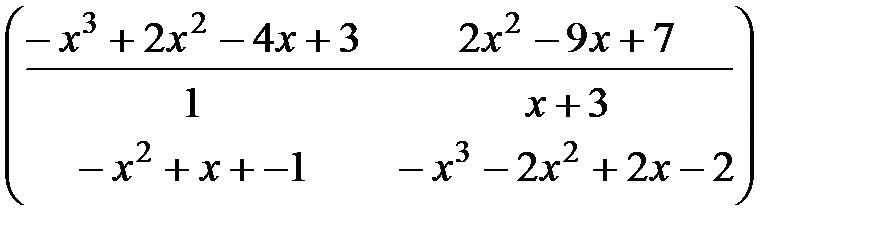 ([2]-
([2]- 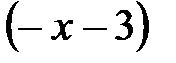 [1]),
[1]), 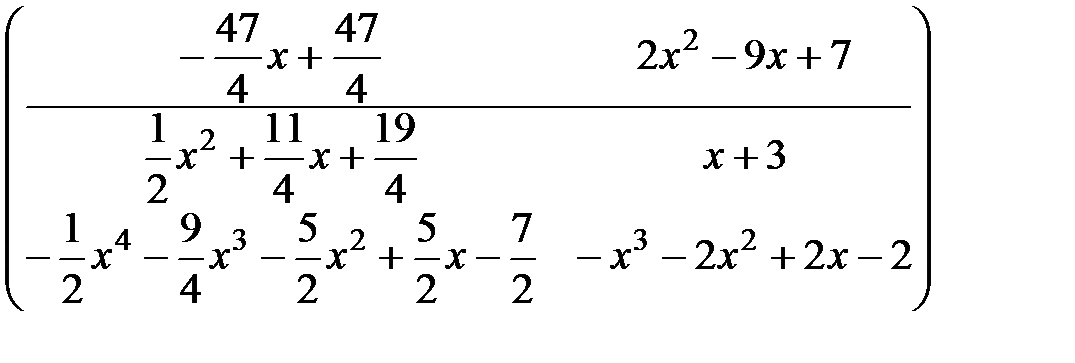 ([1]-
([1]- 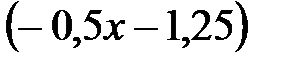 [2]),
[2]), 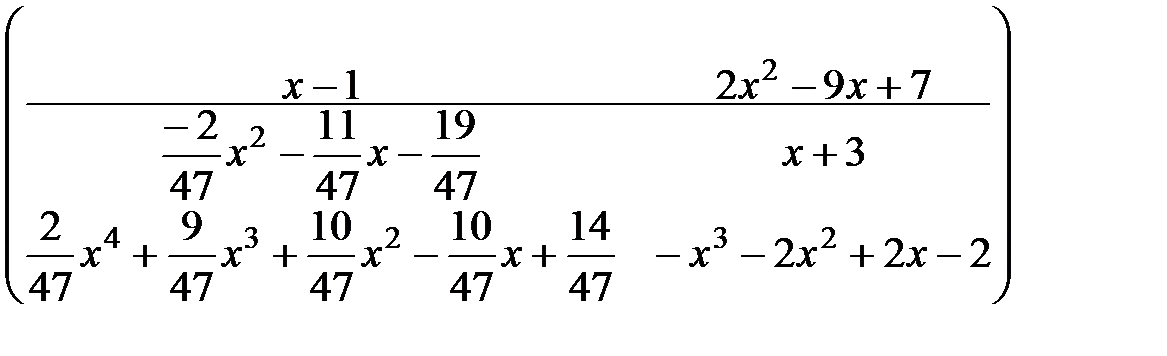 (
(  [1]) придем к равенству
[1]) придем к равенству 
 .
.
Функция вида 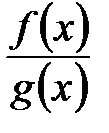 , где
, где  и
и  многочлены, называется рациональной. Пусть ее знаменатель
многочлены, называется рациональной. Пусть ее знаменатель  представляется в виде произведения взаимно простых многочленов
представляется в виде произведения взаимно простых многочленов  . Найдём многочлены
. Найдём многочлены 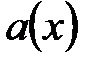 и
и 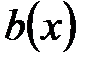 , что
, что  . Умножим равенство на рациональную функцию
. Умножим равенство на рациональную функцию 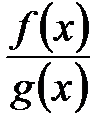 , и сократим дроби. В результате получим равенство
, и сократим дроби. В результате получим равенство  . Тем самым рациональная функция может быть представлена в виде суммы «простейших» рациональных функций.
. Тем самым рациональная функция может быть представлена в виде суммы «простейших» рациональных функций.
|
|
|


