 |
2.1 Упражнения. 3 Интерполяционный многочлен. 4. Если v(x) взаимно просто с многочленами g(x) и f(x), то v(x) взаимно просто с произведением g(x)f(x).
|
|
|
|
2. 1 Упражнения
1. Доказать свойства
1. Если v(x) взаимно просто с g(x), то 
2. Если v(x) взаимно просто с g(x), то 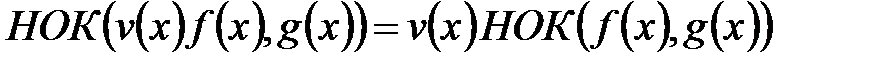
3. 
4. Если v(x) взаимно просто с многочленами g(x) и f(x), то v(x) взаимно просто с произведением g(x)f(x).
5. Если v(x) взаимно просто с произведением многочленов g(x) и f(x), то v(x) взаимно просто с каждым из сомножителей.
6. Для любого v(x) справедливо равенство  .
.
7. Двучлен 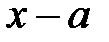 взаимно прост с f(x) тогда и только тогда, когда
взаимно прост с f(x) тогда и только тогда, когда 
2. Найти наибольший общий делитель многочленов
1. 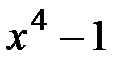 и
и 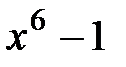
2.  и
и 
3. 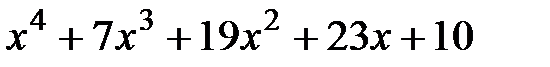 и
и 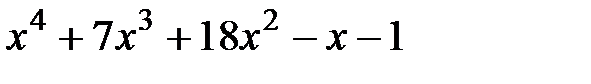
4. 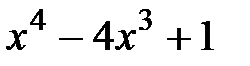 и
и 
5.  и
и 
6.  и
и 
7.  и
и 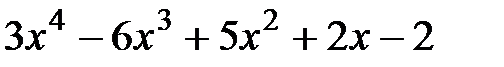
8.  и
и 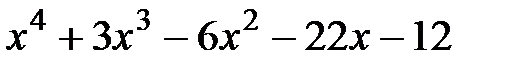
9.  и
и 
10.  и
и 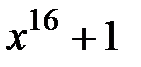
11.  и
и 
12.  и
и 
13. 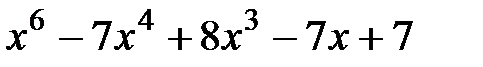 и
и 
14. 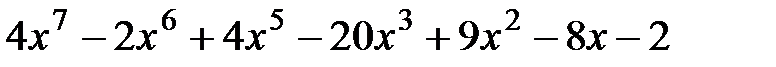 и
и 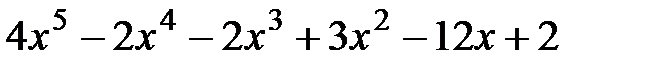
15. 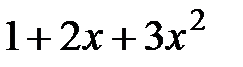 и
и 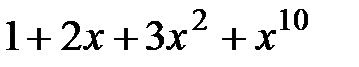
16. 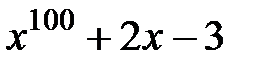 и
и 
17. 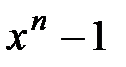 и
и 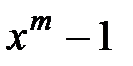
18. 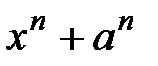 и
и 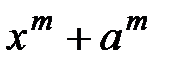
3. Найти наименьшее общее кратное многочленов
1.  и
и 
2. 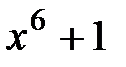 и
и 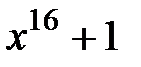
3. 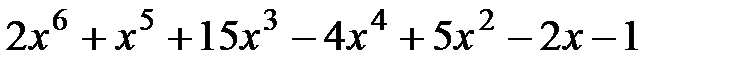 и
и 
4. 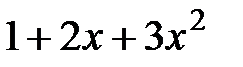 и
и 
5. 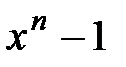 и
и 
6. 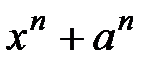 и
и 
4. Найти наибольший общий делитель многочленов f(x) и g(x) и многочлены u(x) и w(x) в представлении u(x)f(x)+w(x)g(x)=НОД(f(x), g(x)).
1. 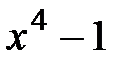 и
и 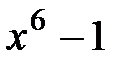
2.  и
и 
3.  и
и 
4. 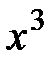 и
и 
5.  и
и 
6. 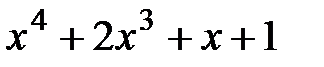 и
и 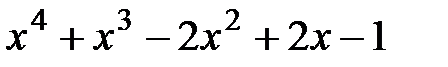
7.  и
и 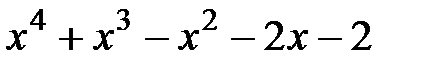
8. 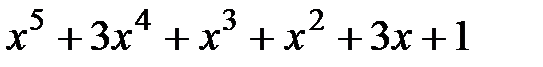 и
и 
9.  и
и 
10.  и
и 
11.  и
и 
12.  и
и 
13.  и
и 
14.  и
и 
15. 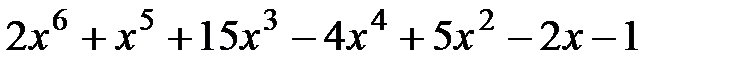 и
и 
16.  и
и 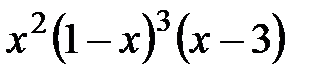
17.  и
и 
18. 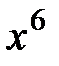 и
и 
19.  и
и 
20.  и
и 
21.  и
и 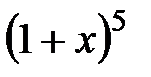
22.  и
и 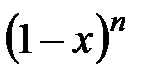
5. Найти многочлен наименьшей степени, дающей в остатке
1.  при делении на
при делении на  и
и  при делении на
при делении на 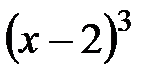
2. 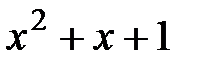 при делении на
при делении на  и
и  при делении на
при делении на 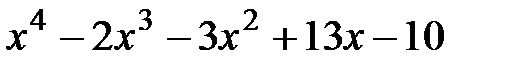
6. Освободиться от иррациональности в знаменателе
1. 
2. 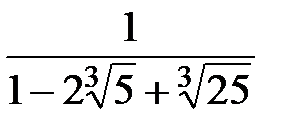
3. 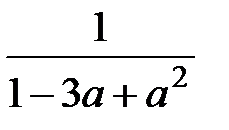 , если
, если 
4. 
5. 
6. 
7. Представить в виде суммы дробей
1. 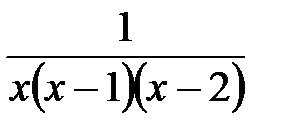
2. 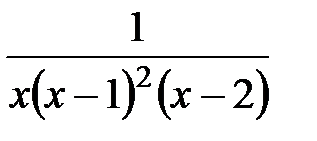
3. 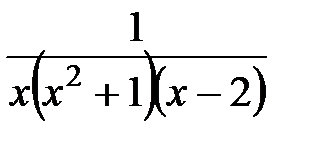
4. 
5. 
3 Интерполяционный многочлен
Задача построения многочлена наименьшей степени, который в заданных точках принимает заданные значения, называется задачей интерполяции. Решение задачи интерполяции называют интерполяционным многочленом.
Пусть требуется построить многочлен, который в точках a1, …, an (n> 1) принимает значения y1, …, yn. Положим w(x)=(x-a1)…(x-an) и 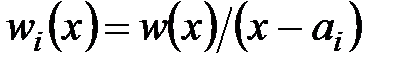 . Легко убедится в справедливости равенств wi(aj)=0 при
. Легко убедится в справедливости равенств wi(aj)=0 при  . Следовательно, многочлен
. Следовательно, многочлен  принимает в точках a1, …, an значения y1, …, yn. Существует единственный интерполяционный многочлен степени не превосходящий n-1, который принимает в точках a1, …, an значения y1, …, yn. . Следовательно,
принимает в точках a1, …, an значения y1, …, yn. Существует единственный интерполяционный многочлен степени не превосходящий n-1, который принимает в точках a1, …, an значения y1, …, yn. . Следовательно,  - интерполяционный многочлен. Представление интерполяционного многочлена в указанном виде называют формой Лагранжа.
- интерполяционный многочлен. Представление интерполяционного многочлена в указанном виде называют формой Лагранжа.
|
|
|
Пусть f(x) – произвольный многочлен. Под разностью первого порядка будем понимать  . Индукцией определим разность порядка k
. Индукцией определим разность порядка k  . Нетрудно проверить следующее выражение разности порядка k
. Нетрудно проверить следующее выражение разности порядка k  . Из полученной формулы вытекает независимость разности от порядка, в котором расположены ее аргументы.
. Из полученной формулы вытекает независимость разности от порядка, в котором расположены ее аргументы.
Если степень многочлена f(x) равна n, то разность 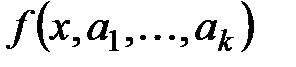 порядка k есть многочлен степени n-k при n
порядка k есть многочлен степени n-k при n 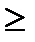 k. Если n< k, то разность порядка k равна нулю. Из определения разности порядка k выводим равенство, позволяющее выразить многочлен через соответствующие разности
k. Если n< k, то разность порядка k равна нулю. Из определения разности порядка k выводим равенство, позволяющее выразить многочлен через соответствующие разности  . При решении задачи интерполяции
. При решении задачи интерполяции  , и, значит, получаем представление интерполяционного многочлена в форме Ньютона
, и, значит, получаем представление интерполяционного многочлена в форме Ньютона  .
.
3. 1 Упражнения
1. Построить интерполяционный многочлен в форме Лагранжа
1. 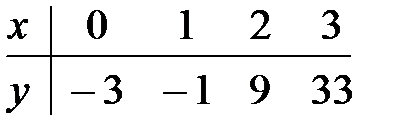
2. 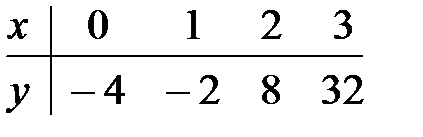
3. 
4. 
5. 
6. 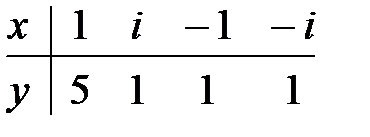
7. 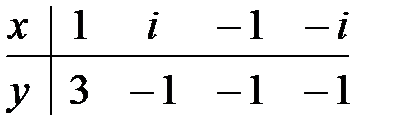
8. 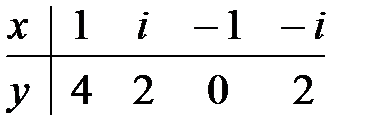
9. 
10. 
11. 
12. 
13. 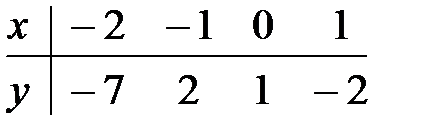
14. 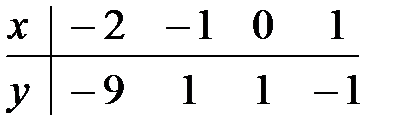
15. 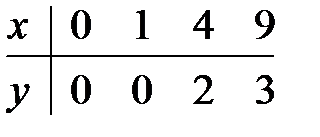
16. 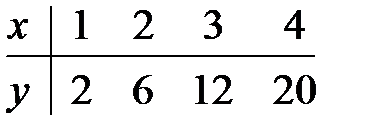
17. 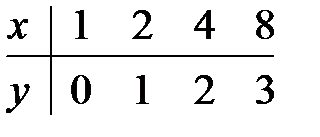
18. 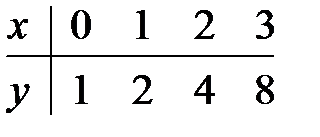
19. 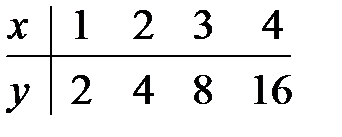
20. 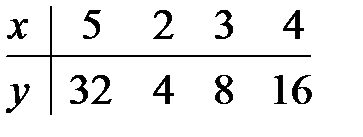
2. Построить интерполяционный многочлен в форме Ньютона
1. 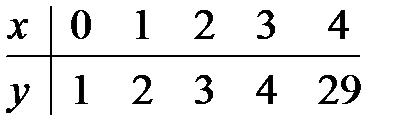
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 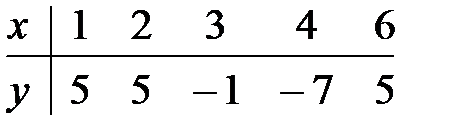
11. 
12. 
13. 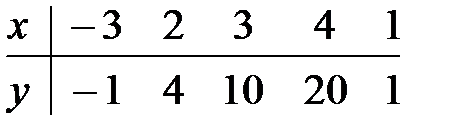
14. 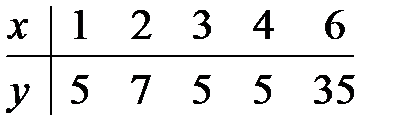
15. 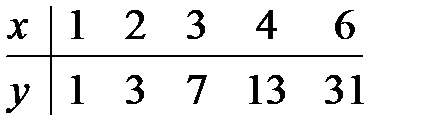
16. 
17. 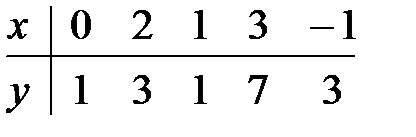
18. 
19. 
20. 
3. Разложить в сумму дробей (с помощью интерполяционного многочлена в форме Лагранжа)
1. 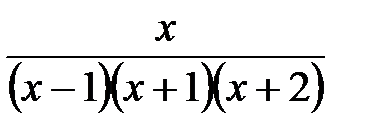
2. 
3. 
4. 
5. 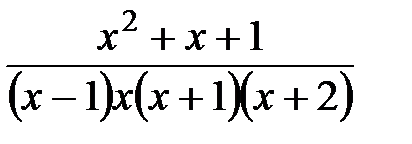
6. 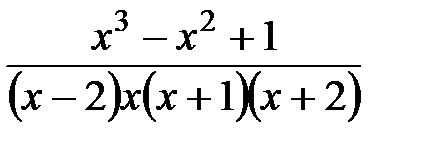
7. 
8. 
9. 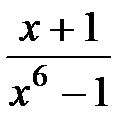
10. 
4. Найти сумму (используя интерполяционный многочлен в форме Ньютона)
1. 
2. 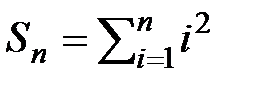
3. 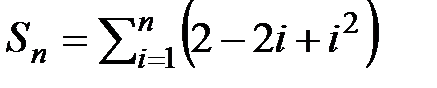
4. 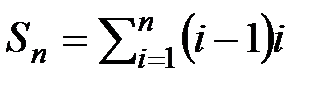
5. 
6. 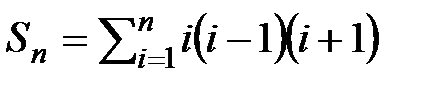
7. 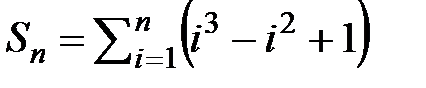
8. 
9. 
10.  ,
, 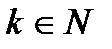
5. Многочлен  при делении на
при делении на 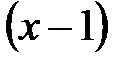 имеет остаток 1, на
имеет остаток 1, на  имеет остаток 3, на
имеет остаток 3, на 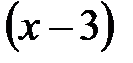 имеет остаток 5, на
имеет остаток 5, на  имеет остаток 6. Какой остаток получится при делении
имеет остаток 6. Какой остаток получится при делении 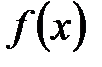 на
на  ?
?
4 Неприводимый многочлен, его свойства
Многочлен называется неприводимым над числовым полем, если он не делится на многочлены меньшей степени (исключая константы) с коэффициентами из этого поля. Многочлен над числовым полем единственным образом раскладывается в произведение неприводимых многочленов, с точностью до перестановки сомножителей и числовых множителей.
|
|
|
Многочлены первой степени неприводимы над любым числовым полем. Число a называется корнем многочлена, если f(a)=0. Многочлен степени n имеет не более n корней. Приведем свойства неприводимых многочленов
A. Если h неприводимый многочлен и fg делится на h, то либо f делится на h, либо g делится на h
B. Если h неприводимый многочлен, то либо f взаимно просто с h, либо f делится на h
C. Если неприводимый многочлен f делится на многочлен h, то 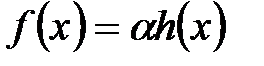 , где
, где  - число
- число
D. Пусть  - неприводимые многочлены и
- неприводимые многочлены и  ,
, 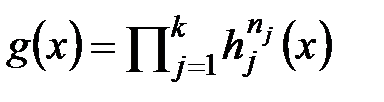 , тогда
, тогда  и
и 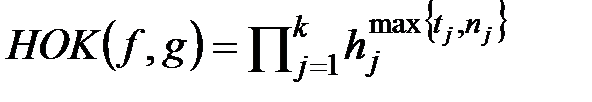 .
.
|
|
|


