 |
5.1 Упражнения. 6 Формальная производная, ее свойства. 7 Формулы Виета, симметрические полиномы
|
|
|
|
5. 1 Упражнения
1. Найти содержание многочлена
1. 
2. 
3. 
4. 
5. 
6. 
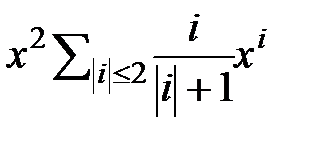
7. 
8. 
9. 
10. 
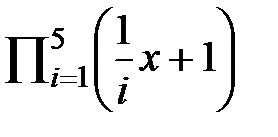
11. 
2. Найти рациональные корни многочлена
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
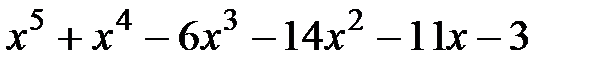
13. 
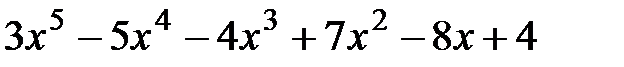
14. 
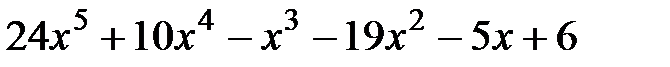
15. 
16. 
17. 
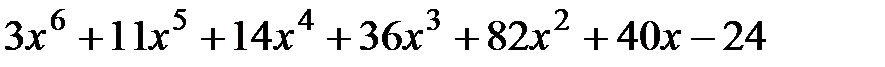
18. 
3. Разложить на неприводимые множители над полем Q
1. 
2. 
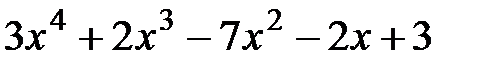
3. 
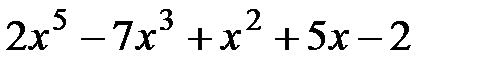
4. 
5. 
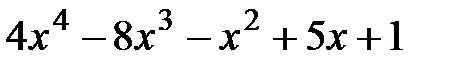
6. 
7. 
8. 
9. 
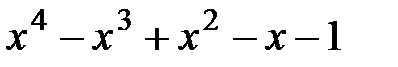
4. Доказать неприводимость многочлена над полем Q
1. 
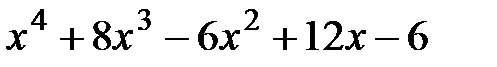
2. 
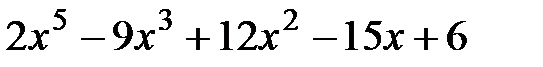
3. 
4. 
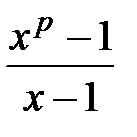, где 
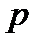- простое
6 Формальная производная, ее свойства
Многочлен f(x+y)-f(x) делится на y без остатка. Положим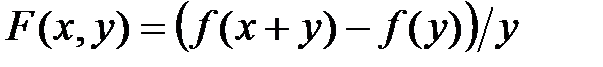 
. Многочлен F(x, 0) называют производной многочлена f(x) и обозначают 
. Приведем свойства производной
A. 
B.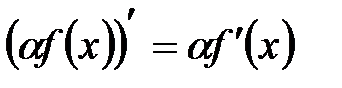 
C.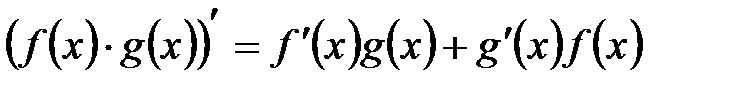 
D. 
Если f(x) делится на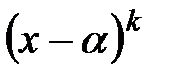 
и не делится на 
, то говорят, что 
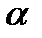корень многочлена f(x) кратности k. Между кратными корнями многочлена и его производной существует связь. Если a корень многочлена f(x) кратности k, то a корень его производной кратности k-1.
Пусть 
- многочлен с коэффициентами из поля P. Построим многочлен 
, коэффициенты которого принадлежат P. Рассмотрим многочлены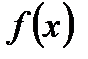 
и 
над полем разложения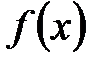 
, которое обозначит через T. Пусть 
- разложение многочлена 
над T. Тогда, по теореме о кратных корнях 
и 
. Пусть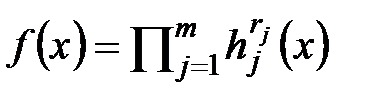 
- разложение многочлена 
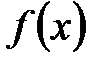над полем P на неприводимые множители, тогда 
. То есть, многочлен 
раскладывается на те же неприводимые множители, что и 
, причем кратность каждого множителя равна 1.
Производную порядка k от многочлена f(x) обозначим 
. Будем считать, что 
- исходный многочлен. При вычислении производных высокого порядка от произведения справедлива формула, напоминающая бином Ньютона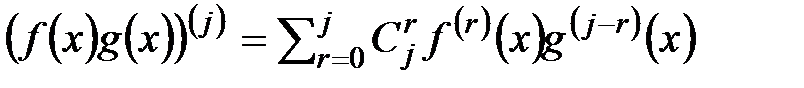 
.
Для многочлена 
степени n справедлива формула Тейлора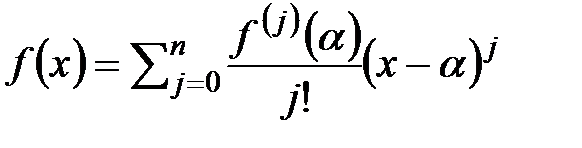 
. В частности отсюда вытекает возможность вычисления значения производной j-го порядка в точке 
по схеме Горнера. Другим важным фактом является эквивалентное определение кратного корня с помощью производной. Условие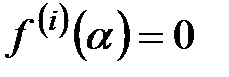 
при i=0, …, k-1 и 
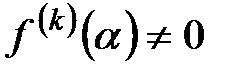равносильно тому, что 
- корень f(x) кратности k.
|
|
|
Рассмотрим обобщение задачи интерполяции. Требуется найти многочлен наименьшей степени, у которого на некотором множестве заданы не только его значения, но и значения производных до определенных порядков. Пусть на множестве точек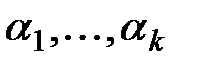 
заданы значения функции, а также её производных высших порядков. То есть, заданы значения 
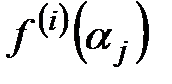, где j=1, …, k и 
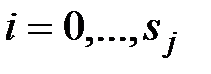. Задача заключается в построении многочлена 
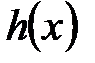наименьшей степени, удовлетворяющего равенствам 
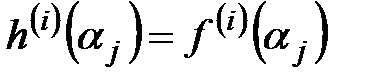, где j=1, …, k и 
. Положим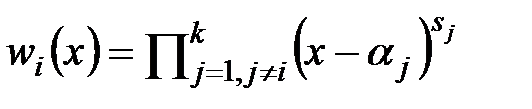 
. Будем искать интерполяционный многочлен в виде 
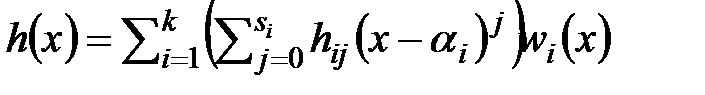, где коэффициенты 
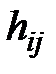определяются из условий задачи интерполяции. Поскольку 
, то имеем рекуррентные формулы для вычисления 
: 
, и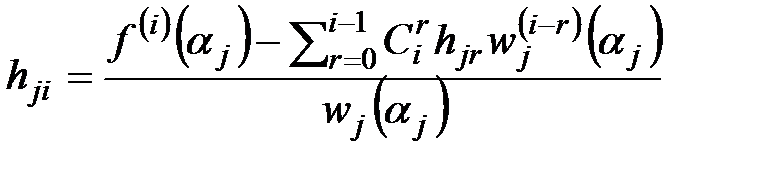 
, где j=1, …, k и 
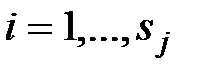. Интерполяционный многочлен, записанный в виде 
, называется интерполяционным многочленом Лагранжа – Сильвестра. Существует единственный многочлен h(x) степени не больше 
, удовлетворяющий равенствам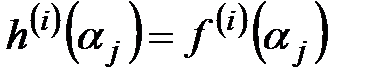 
, где j=1, …, k и 
.
6. 1 Упражнения
1. Разложить в формулу Тейлора в точке 
1. 
, 
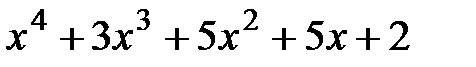2. 
, 
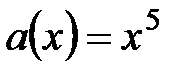3. 
, 
4. 
, 
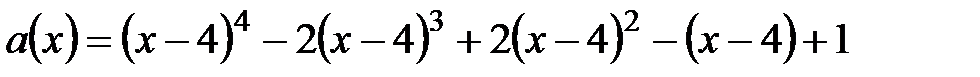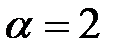
5. 
, 
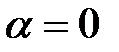
2. Отделить кратные множители
1. 
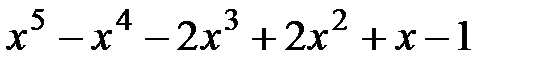
2. 
3. 
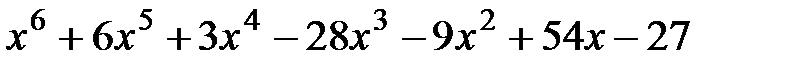
4. 
3. Определить кратность корня 
1. 
2. 
4. Построить интерполяционный многочлен Лагранжа-Сильвестра
1. 
, 
, 
, 
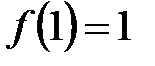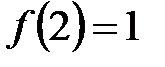
2. , 
, 
, 
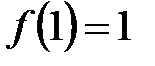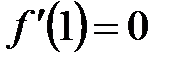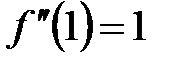3. 
, 
, 
, 
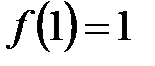4. 
, 
, 
, 
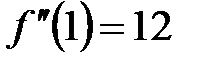5. 
, 
, 
, 
, 
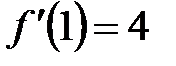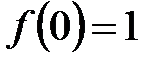5. Найти многочлен наименьшей степени, дающий в остатке
1. 
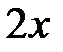при делении на 
и 
при делении на 
2. 
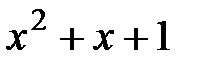при делении на 
и 
при делении на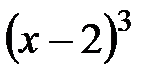 
6. При каких a, b, c многочлен 
имеет -1 корнем не ниже третьей кратности?
7. При каких a, b многочлен имеет кратный корень
1. 
2. 
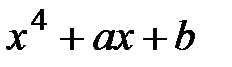
3. 
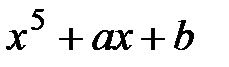
4. 
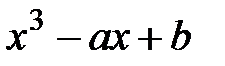
5. 
6. 
7. 
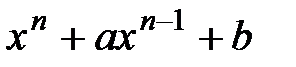
8. Показать, что многочлен 
, где 
не имеет корней кратности выше 2.
9. Показать, что многочлен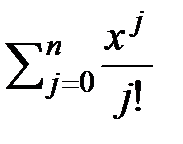 
не имеет кратных корней.
7 Формулы Виета, симметрические полиномы
Пусть многочлен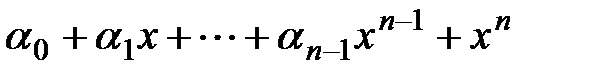 
имеет корни 
. Из равенства 
, сопоставив коэффициенты при равных степенях, выводим формулы Виета 
.
|
|
|
Многочленом от n переменных называется функция вида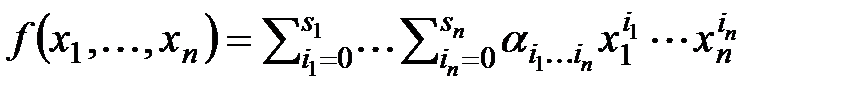 
. Степенью многочлена называется максимальная суммарная степень по всем переменным. Слагаемое вида 
называется мономом. Многочлен от n переменных может содержать несколько мономов максимальной степени. Моном максимальной степени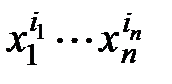 
назовём старшим, если набор его степеней 
лексикографически максимален. Обозначим через v(f) набор степеней старшего монома. Имеет место v(fg)=v(f)+v(g),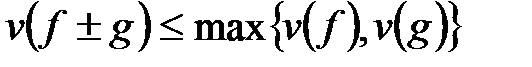 
. Многочлен от нескольких переменных называется симметрическим, если он не меняется при любой перестановке переменных. Многочлены 
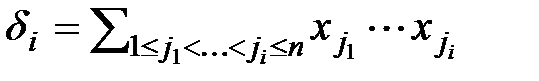, где i=1, …, n называются элементарными симметрическими многочленами.
По формулам Виета, коэффициенты многочлена с точностью до знака суть значения элементарных симметрических многочленов от его корней. Заметим 
. Для любого симметрического многочлена f степени 
, справедливы неравенства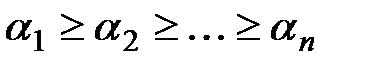 
. Степень 
равна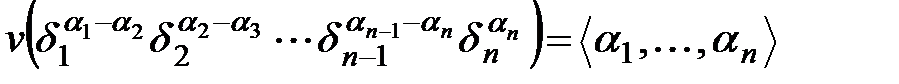 
. Из этих фактов вытекает основная теорема алгебры симметрических многочленов.
Любой симметрический многочлен единственным образом представляется в виде полинома от элементарных симметрических многочленов.
Хотя доказательство теоремы носит конструктивный характер, для построения искомого полинома используют метод неопределенных коэффициентов.
Например, рассмотрим задачу вычисления суммы кубов корней уравнения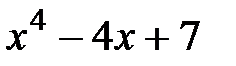 
. Обозначим через 
корни этого уравнения. По теореме Виета, известны значения элементарных симметрических многочленов на этих корнях 
, 
, 
, 
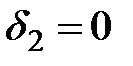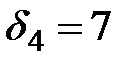. Многочлен 
является симметрическим, и, значит, представляется в виде многочлена от элементарных симметрических многочленов. Поскольку исходный многочлен имеет степень 3, то его представление имеет вид 
, где 
- неизвестные коэффициенты. Чтобы найти эти коэффициенты возьмем конкретные значения переменных , сосчитаем на них значения элементарных многочленов и приравняем значение многочлена и его представления. При удачном выборе , из полученного равенства будет найден один из коэффициентов. Данные удобно свести в таблицу 
. Таким образом, 
. Подставим в правую часть значения элементарных симметрических многочленов на корнях многочлена, находим, что сумма кубов корней этого уравнения равна 12.
|
|
|
