Лабораторная работа № 1. Вводная часть. Теоретическая платформа выполнения работы

Лабораторная работа № 1

 

Тема лабораторного занятия: «Анализ расчетных алгоритмов и величин селекционного дифференциала и показателя интенсивности отбора»

 

Ключевые слова: лесная селекция, популяция, структура популяции, дисперсия значений признака, отбор, критерии отбора, эффективность отбора, эффект отбора, селекционный дифференциал, интенсивность отбора.

 

Методические параметры лабораторного занятия.

Бюджет рабочего времени – 6 часов.

Количество двухчасовых занятий – 3.

Распределение бюджета рабочего времени:

-   1 час на постановку задачи и освоение теоретических основ и принципов определения оценок эффекта отбора;

-   1 час на расчеты базовых оценок селекционного дифференциала и показателя интенсивности отбора в электронных таблицах Microsoft Excel.

-   2 часа на расчеты в электронных таблицах Microsoft Excel оценок селекционного дифференциала и интенсивности отбора, построение диаграмм и визуализацию структуры исходных популяций (совокупностей), анализ влияния структуры (характера распределения особей) популяции на величину оценок эффективности отбора;

-   1 час на расчеты в электронных таблицах Microsoft Excel оценок селекционного дифференциала и интенсивности отбора, построение диаграмм и визуализацию структуры исходных популяций (совокупностей), анализ влияния дисперсии (степени разброса значений) селектируемого признака в популяции на величину оценок эффективности отбора;

-   1 час на расчеты в электронных таблицах Microsoft Excel оценок селекционного дифференциала и интенсивности отбора, анализ влияния степени напряженности отбора (заданной жесткости отбора «лучших» особей) в популяции на величину оценок эффективности отбора;

 

Дидактический материал, необходимый для проведения данной лабораторной работы, приведен в файлах электронных таблиц Excel – «Образец Дифференциал» (Приложение – 1. 1) и «Рабочий Дифференциал» (Приложение 1. 2).

 

 

Вводная часть

Оценка эффективности отбора представляет собой одну из важных задач селекции, в частности селекции методом отбора или аналитической селекции. При решении задач синтетической селекции (селекция методом гибридизациии) весьма ответственным этапом выступает сравнительная оценка полученных гибридов и определение меры их превосходства над родительскими формами или ранее полученным селекционным материалом. Аналогичные заключения можно сделать в отношении реализуемых селекционных программ, предусматривающих применение таких методов как мутагенез или полиплоидия. В каждом из этих случаев для оценки эффективности проводимых селекционных мероприятий используют специальные оценочные критерии, называемые селекционным дифференциалом и интенсивностью отбора.

 

 

Теоретическая платформа выполнения работы

Проведение отбора по фенотипу, в частности отбора плюсовых деревьев, потомство которых используется для создания лесосеменных плантаций первого поколения (ЛСП-1), будет эффективным при высоком уровне аддитивной (не связана с эффектом доминирования) наследственности, а также будет зависеть от проявления эффекта доминирования (полного или неполного). В общем, этот фактор рассматривают как генотипический.

Аддитивная наследственность в селекции рассматривается как наследственность, обусловленная собственно набором генов, без учета эффекта их аллельного (доминирование) и межаллельного (эпистаз, плейотропия, комплементарность) взаимодействия. Такая наследственность часто называется истинной и оценивается коэффициентом наследуемости в узком смысле. Аддитивная наследственность – это наследственность, обусловленная суммирующим эффектом полимерно действующих генов.

Кроме того, эффективность отбора будет определяться тем, насколько велико влияние факторов среды на формирование фенотипических признаков, т. е. будет зависеть от так называемой средовой компоненты общей фенотипической вариансы или дисперсии признака, вызванной пестротой экологических условий (в общем смысле, пестротой фона факторов среды).

Результативность отбора и достигаемый в ходе его проведения эффект определяется еще и заданным уровнем отбора (заданной «жесткостью» или «строгостью отбора»), который в свою очередь определяется задачами селекции и принятым в каждом конкретном случае порядком проведения селекционных мероприятий. В конечном итоге это уровень определяется селекционером. Уровень интенсивности отбора зависит от того, сколько наилучших особей будет отобрано из популяции (из исходной совокупности в общем случае), например: 15 самых лучших или 10 самых лучших, или только 5 самых лучших, или в конечном итоге только одно самое лучшее дерево. Он (уровень интенсивности отбора) также определяется тем, какой предел проявления признака признается достаточным для включения особи в число отобранных, например: все особи с высотой 32 м и более, или все особи с высотой 33 м и более, или, наконец, все особи с высотой 35 м и более и т. д.

Для популяций древесных и кустарниковых пород (вообще видов древесных растений, включая декоративные и плодовые) характерно промежуточное наследование, что связано с аддитивной наследственностью большинства количественных признаков и определено эволюционным процессом в аллогамных (перекрестно опыляемых) популяциях. Аддитивный характер наследования основных количественных признаков деревьев и кустарников приводит к возникновению множества постепенно переходящих друг в друга количественных его проявлений (принято считать: чем больше полимерно действующих генов, тем сильнее проявление признака).

При отборе по фенотипу (отбор плюсовых деревьев и насаждений в лесной селекции) результат будет определяться рядом условий:

- тем, насколько велика доля наследственной обусловленности проявлений признака или, что то же самое, генотипической обусловленности изменчивости признака, в общей, учитываемой нами при отборе фенотипической изменчивости признака у селектируемых особей, от степени генетической детерминированности признака, от степени его стабильности;

- тем, какова доля средовой дисперсии признака или доля влияния факторов среды на его проявление, от его лабильности, от подверженности признака влиянию факторов среды;

- в конечном итоге фенотипическое проявление признака, то на что направлен отбор по фенотипу, будет зависеть от соотношения долей влияния на проявление фенотипа факторов наследственности (генотипа или идиотипа в широком смысле) и факторов среды (доля ненаследственной изменчивости).

 

Это позволяет рассматривать взаимное действие (оно всегда именно таково) факторов среды и факторов наследственности на формирование фенотипа особи как действие одного фактора – фактора соотношения между долями влияния среды и генотипа. Тогда эффект отбора по количественным признакам можно представить как результат, зависящий от действия двух комплексных факторов:

- от интенсивности отбора, определяемой задачами селекции и планом селекционных мероприятий;

- от силы модифицирующего влияния среды, под которой понимают долю ненаследственной изменчивости в общей фенотипической изменчивости, рассматривая её как оценку соотношения «наследственность/среда».

 

Для планирования процесса отбора и прогнозирования его результатов важно дать оценку влияния этих двух факторов. В контексте этого эффективность или результативность отбора можно оценить двумя широко применяемыми показателями:

- показателем селекционного дифференциала (обозначим его S );

- показателем интенсивности отбора (обозначим его i ).

 

Относительную силу (долю) воздействия генетического влияния и влияния внешней среды на фенотипическое проявление признака оценивают (измеряют) с помощью коэффициента наследуемости (H²), который выражается в долях от единицы или в процентах (%%). Например, Н² = 0, 78 или 78%. Это значит, что проявление признака на 78% обусловлено генотипически, а на 22% – условиями среды. Определение понятия селекционный дифференциал приведено ниже.

Селекционный дифференциал – это разность между средней величиной признака в совокупности отобранных особей и соответствующей его (признака) средней величиной в исходной популяции.

 

ПРИМЕР. В лесном хозяйстве отобранными лучшими растениями являются плюсовые деревья, выделенные по комплексу положительных фенотипических признаков, имеющих хозяйственное и адаптационное значение, их семенное потомство (полусибсовые семьи), клоновые репродукции (прививочные плантации и архивы клонов). Если средняя высота деревьев в насаждении (популяции) составляет 30 метров, а средняя высота группы отобранных плюсовых деревьев составляет 33 метра, то селекционный дифференциал составит: 33м – 30м = 3 м, или 10% (от исходной популяционной величины). Если при испытании семенного потомства (испытательные культуры в ГБУ НО «Семеновский спецсемлесхоз» в п. Осинки) средняя высота всего потомства в испытательных культурах 20 м, а высота отобранного потомства от одного плюсового дерева – 21 м, то селекционный дифференциал равен 21м – 20м = 1 м, или 5%.

 

Количественное выражение величины селекционного дифференциала традиционно вычисляют по приведенной ниже формуле (1).

 

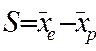, где                                                                                   (1)

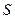-  – селекционный дифференциал;

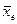-  – среднее значение признака в отобранной группе растений (индекс е от extraction – выделение, экстракция);

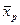- – среднее значение признака в популяции, из которой отобрана группа особей (индекс р от population – популяция).

 

Выражают селекционный дифференциал в натуральных единицах измерения значений признака, например: высота – в м; диаметр ствола на высоте 1. 3 м – в см; объем ствола – в м³; площадь поперечного сечения ствола – в см² и т. д. При этом могут также использоваться как относительные размерные показатели (отношение высоты ствола, выраженной в метрах к площади поперечного сечения ствола, выраженной в см² – м/см²; плотность древесины – г/см³ и т. д. ), так и безразмерные величины (отношение длины листовой пластинки, выраженной в см, к ширине листовой пластинки, выраженной в сантиметрах, называется коэффициентом формы и выражается безразмерной величиной; аналогично выражается коэффициент формы шишек или семян и т. п. ). Эта форма выражения селекционного дифференциала наиболее предметна, наглядна и легко воспринимается. Она позволяет оценить эффективность отбора, проводимого на разных объектах, но только по одному и тому же показателю, например, по высоте ствола или его объему. Вместе с тем понятно, что такая форма выражения селекционного дифференциала не позволяет сопоставлять эффективность отбора, проводимого по разным признакам: высоте ствола (в метрах) и диаметру ствола (в сантиметрах), даже если отбор ведется в одной и той же популяции.

В этой связи для получения сопоставимой оценки эффективности отбора, проводимого по разным признакам, селекционный дифференциал выражают в процентах от среднего значения признака в исходной совокупности – в популяции, из которой проведен отбор. Понятно, что при такой оценке в относительных величинах (процент от числа есть величина относительная или доля) дать сравнительную оценку эффективности отбора любых самых разных признаков, и указать, по какому признаку отбор оказался более эффективным, а по какому – менее эффективным, достаточно просто.

Однако, хорошо известно то, что оценка эффективности отбора зависит от дисперсии признака. Тогда сравнение эффективности отбора по признакам, имеющим разную дисперсию, будет не вполне корректным, даже если её оценку выразить в процентах. Понятно, что по признаку с большей дисперсией, будет достигнут и заведомо больший результат, и, наоборот – для признака с меньшей дисперсией результат окажется меньшим. Для преодоления этого обстоятельства при получении сопоставимых оценок эффективности отбора используют показатель, называемый интенсивностью отбора. Он представляет собой отношение величины селекционного дифференциала, выраженного в натуральных единицах измерения, к величине дисперсии признака в исходной популяции, из которой был произведен отбор, также выраженной в натуральных величинах. Величина вычисляется по формуле (2):

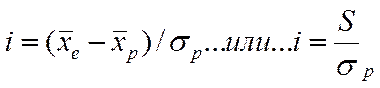, где                        (2)

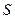-  – селекционный дифференциал;

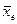-  – среднее значение признака в отобранной группе растений (индекс е от extraction – выделение, экстракция);

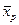- – среднее значение признака в популяции, из которой отобрана группа особей (индекс р от population – популяция);

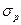-  – среднеквадратическое значение признака в исходной популяции.

Легко заметить, что показатель интенсивности отбора есть величина относительная и безразмерная, поскольку в получаемом отношении участвуют только одноразмерные величины: разность средних значений и среднеквадратическое отклонение признака в исходной популяции.

Также следует учитывать, что, чем интенсивнее ведется отбор, тем выше значение селекционного дифференциала. При этом, в практической селекции традиционно стремятся к повышению селекционного дифференциала.

Селекционный дифференциал можно рассматривать как функцию числа отобранных деревьев (или семенных семей, или клонов) и числа деревьев (или семей, или клонов), из которых провели отбор. При большем отношении числа изученных исходных деревьев (числа деревьев в популяции, которая подверглась отбору) к отобранным деревьям селекционный дифференциал выше. Однако связь между ними не прямая. Джонатан В. Райт (1978, стр. 161) в своей работе приводит таблицу взаимоотношения между селекционным дифференциалом и числом деревьев в популяции, которое следует изучить при отборе – то количество объектов в исходной совокупности, которая может выступать объектом отбора (табл. 1. 1).

 

Таблица 1. 1.

Связь между селекционным дифференциалом (в долях от стандартного отклонения) и числом деревьев, которые надо изучить (учесть) при отборе,

в котором отбирают только одно лучшее дерево

(по Дж. В. Райту, 1978)

 

Селекционный дифференциал	Число деревьев	Селекционный дифференциал	Число деревьев	Селекционный дифференциал	Число деревьев
1, 0		2, 5		4, 0
1, 5		3, 0		5, 0
2, 0		3, 5		6, 0

 

Несложно заметить, что отношение следует увеличить приблизительно в 10 раз, для того чтобы селекционный дифференциал стал равен 2 σ, а не 1 σ; для того, чтобы селекционный дифференциал увеличить с 2 до 3 величин стандартных отклонений число деревьев должно быть увеличено в 17, 6 раза, а для того, чтобы селекционный дифференциал возрос с 3 до 4 стандартных отклонений число деревьев необходимо увеличить в 42, 7 раза. Следует иметь в виду, что приведенные в таблице 1. 1 величины достоверны только в том случае, если отбор проводят в сходных условиях. Как видим, на практике может возникнуть ограничение селекционного дифференциала, вызванное большой трудоемкостью работ и обширными площадями обследований. Тем не менее, практически всегда можно сравнить деревья, растущие в нескольких десятках метров одно от другого, и предположить (с той или иной степенью вероятности), что выбрано самое лучшее из них. Ограничение величины селекционного дифференциала целесообразно и в целях экономии: слишком дорого обходится обследование сотен или тысяч гектаров для отбора одного дерева. С увеличением требований к отбору селекционный дифференциал возрастает. Если отбор будет вестись интенсивнее, и отбирать будут не 5 – 7 лучших деревьев из популяции, а 3 или 1, его результат (средние значения признаков в группе отобранных особей) будет выше.

 

ЗАДАНИЕ 1. Рассчитайте величину оценок эффективности отбора: селекционного дифференциала и интенсивности отбора по предложенным заданиям (задания прилагаются в форме дидактического материала).

Задание 1 выполняется по дидактическому материалу, представленному в файле электронных таблиц Excel: «Образец Дифференциал» и «Образец Дифференциал» (Приложение 1. 1. и 1. 2). Варианты дидактического материала для расчета величин достигнутого при отборе селекционного дифференциала и показателя интенсивности отбора определяются преподавателем или могут быть предложены обучающимся по материалам его собственных исследований.

 

Порядок выполнения расчетов. Данное задание предусматривает решение 3 задач, которые имеют общую методическую базу и предусматривают определение факта наличия и анализ характера влияния на величину селекционного дифференциала таких его условий как:

- дисперсия признака в популяции из которой осуществляется отбор;

- структура распределения особей в популяции в зависимости от проявления признака, на который направлен отбор;

- напряженность режима отбора или его жесткость, которая определяется условиями селекции или, в конечном итоге, селекционером.

 

1. На первом этапе рассчитывают средние значения одного из селектируемых признаков в группе отобранных особей (совокупности плюсовых растений), и для исходной популяции в целом (исходного насаждения). Применяют общепринятый алгоритм расчетов с определением следующих основных статик (3):

 

 

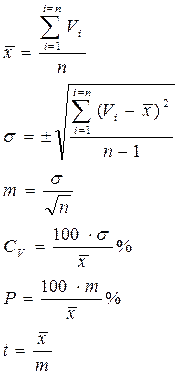
                                                                                                  (3)

 

, где:

 

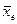-  – среднее значение признака в отобранной группе растений;

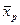- - среднее значение признака в популяции, из которой отобрана группа особей;

- V_i – даты или варианты наблюдений, отдельные измерения – частные значения признака;

- e - индекс отобранной группы (от слова extraction – экстракция, выделили, отобрали);

- p – индекс, обозначающий принадлежность к популяции (от слова population – популяция);

- ∑ – знак суммы;

- i – порядковый номер варианта, i= от 1 до n;

- n – численность статистической совокупности (для популяции n равно численности популяции; для отобранной группы отселектирванных особей n равно числу отобранных особей; в ситуации, когда параметры популяции оценивают по результатам анализа выборки, численность совокупности – это численность особей на пробной площади, то есть численность выборки);

- σ – среднеквадратическое отклонение (в электронных таблицах Excel – это стандартное отклонение), которое показывает, на сколько в среднем в ту или иную сторону от среднего статистического значения признака отклоняется каждое отдельное частное значение признака в выборке, которое может быть больше или меньше среднего (что показывает знак ±);

- m – ошибка репрезентативности выборочного среднего, показывает на какую величину в большую или меньшую сторону от генерального среднего может отличаться вычисленное среднее для конкретной выборки.

- C_v – коэффициент вариации, показывает какую долю от среднего (в %) составляет величина среднего квадратического отклонения - σ.

- P – точность опыта или относительная ошибка.

- t – критерий достоверности Стьюдента показывает во сколько раз величина среднего превосходит свою ошибку репрезентативности (t – это величина относительная, зависящая от численности выборки и заданной точности, требует сравнения с табличным значением, которое приводится во всех учебниках статистики).

 

2. На следующем этапе для уточнения статистической достоверности разности между результатом отбора и средними популяционным значением признака используется формула (4) достоверности разности двух средних (для случаев парного сравнения):

 

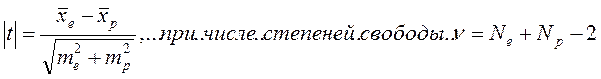(4)

 

где:

- ν – число степеней свободы;

- ν = N_e + N_p – 2  =  (N_e – 1) + (N_p – 1);

- N_e – численность группы отобранных «лучших особей»

- N_p – численность исходной популяции (совокупности).

Если вычисленное значение t-критерия (опытное) больше его табличного значения для определенного числа степеней свободы и заданного уровня точности, то различия между средними можно признать достоверными. Об этом делают соответствующую запись в тетради и на рабочем листе электронных таблиц. Такая ситуация в смысловом отношении означает то, что отбор действительно привел к изменению средних значений селектируемого признака, то, что величина полученного селекционного материала достоверно превышает среднее популяционное значение того же признака в исходной популяции, из которой был осуществлен отбор. Это соответствует тому, что разница между средними значениями признака превышает величину случайных отклонений, не связанных с действием рассматриваемого фактора (в нашем случае с действием отбора). Это является подтверждением результативности отбора.

3. Далее производят соответствующие вычисления селекционного дифференциала по приведенной ранее формуле. Величину селекционного дифференциала выражают как в натуральных величинах: размерных (м, см, кг, г, шт. и др. ) или безразмерных (при относительных или производных признаках), так и в процентах от средней популяционной величины. Результаты записывают в тетрадь или на рабочий лист электронных таблиц Excel.

4. После этого вычисляют значения показателя интенсивности отбора по приведенным выше формулам. Полученный материал интерпретируют, о чем делают соответствующие записи в тетради или на рабочем листе электронных таблиц Excel.

5. В предложенной преподавателем директории на персональном компьютере (например, на рабочем листе электронных таблиц Excel) формируют массивы исходных данных для их статистической обработки и последующего расчета селекционного дифференциала и показателя интенсивности отбора. Обработку ведут в одном из алгоритмических языков или используют возможности электронных таблиц Excel.

6. Производят обработку цифровых массивов данных с получением итоговых результатов и выведением их на печать. Распечатку результатов приобщают к контрольному листу задания или к отчету о выполнении расчетно-аналитической работы.

7. Трансформируют исходный цифровой массив (индивидуальное задание может быть представлено в виде распечатанного текста или в иной форме) в массив таблицы Excel либо получают массив у преподавателя.

8. Выбирают соответствующий алгоритм расчета в библиотеке Excel и осуществляют обработку. Результаты выводят на печать, а распечатку результатов приобщают к курсовому проекту (курсовой или расчетно-графической работе).

9. Повторите весь цикл расчетов для второй популяции того же вида, по тому же признаку. Желательно подобрать второй пример таким образом, чтобы популяции имели одинаковые средние значения признака, но различались бы по показателям дисперсии (размах варьирования, характер распределения особей, сдвиг общего диапазона изменчивости одной из популяций по отношению к другой в ту или иную сторону).

 

ЗАДАНИЕ 2. По предложенным заданиям (задания прилагаются в форме дидактического материала) определите факт наличия и характер влияния на эффективность отбора (на величину оценок селекционного дифференциала и показателя интенсивности отбора) нижеприведённых факторов – условий проведения отбора:

- дисперсии признака в исходной популяции,

- структуры распределения особей в популяции в соответствии с проявлением селектируемого признака,

- напряженности режима отбора.

 

Задание 2 также выполняется по дидактическому материалу, представленному в файле электронных таблиц Excel: «Образец Дифференциал» и «Образец Дифференциал» (Приложение 1. 1. и 1. 2). Варианты дидактического материала для расчета величин достигнутого при отборе селекционного дифференциала и показателя интенсивности отбора определяются преподавателем или могут быть предложены обучающимся по материалам его собственных исследований. Выполнение задания 2 предполагает последовательное решение трех тематических задач, которые приведены ниже.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: