 |
Лабораторная работа № 3. Вводная часть. Порядок проведения занятия
|
|
|
|
Лабораторная работа № 3
Тема: «Анализ эффективности вычисления коэффициента наследуемости в ходе применения двухфакторного иерархического дисперсионного анализа»
Ключевые слова: дисперсия, варианса, дисперсионное отношение, дисперсионный анализ, иерархия, иерархические комплексы.
Методические параметры лабораторного занятия.
Бюджет рабочего времени – 4 часа.
Количество двухчасовых занятий – 4.
Распределение бюджета времени:
- 1 час на освоение теоретических основ и принципов определения оценок наследственно обусловленной части общей фенотипической дисперсии селектируемого признака с применением двухфакторного иерархического дисперсионного анализа;
- 1 час на освоение расчетных алгоритмов вычисления оценок коэффициента наследуемости с помощью двухфакторного иерархического дисперсионного анализа.
- 1 час на расчет в электронных таблицах Microsoft Excel значений коэффициента наследуемости в широком смысле с помощью двухфакторного иерархического дисперсионного анализа равномерных дисперсионных комплексов.
- 1 час на расчет в электронных таблицах Microsoft Excel значений коэффициента наследуемости в широком смысле с помощью двухфакторного иерархического дисперсионного анализа неравномерных дисперсионных комплексов.
Дидактический материал, необходимый для проведения данной лабораторной работы, приведен в файлах электронных таблиц Excel – «Коэффициент наследуемости Двухфакторный анализ» (Приложение – 3. 1).
Вводная часть
Основное назначение дисперсионного анализа – это разложение общей изменчивости признака на изменчивость частную, возникающую в совокупности объектов (у членов популяции или между раметами клонов на ЛСП) под влиянием многообразных факторов. Указанное свойство дисперсионного анализа имеет большое значение при анализе изменчивости, наблюдаемой у биологических объектов, в том числе и у древесных растений и кустарников.
|
|
|
Второе свойство дисперсионного анализа заключается в том, что он позволяет определить статистическую достоверность доли влияния изучаемых факторов. Важной особенностью дисперсионного метода является то, что его можно применять на разных типах выборок (больших и малых) и, что особенно важно, он позволяет обрабатывать совокупности, включающие в себя разнородный материал: разнополые особи у двудомных растений (тополя, ивы, облепиха и др. ); совокупности, состоящие из групп особей растений разного генетического происхождения (особи из естественных насаждений, гибриды, сорта и т. п. ). При этом дисперсионный анализ является методом анализа количественной информации (преимущественно).
При проведении дисперсионного анализа исходят из предположения о том, что некоторая совокупность объектов под действием какого либо фактора (или нескольких факторов) разделяется на несколько (две и более) групп. При этом каждая из групп объектов отличается от других групп величиной среднего группового значения признака и характером его изменчивости – дисперсией или вариансой (вариансный анализ) в пределах группы. Учитывается также и то, что изменчивость признака у объектов возможна как внутри таких групп, так и между ними.
Если в имеющейся совокупности объектов изменчивость (рассеянье, дисперсия) признака в любой из её частей одинакова, то совокупность не разделена на группы. Совокупность признается однородной. Это единая совокупность – одно и тоже. Если же разные части анализируемой совокупности характеризуются разными дисперсиями – разным характером рассеянья признака – то совокупность не рассматривается как единая, и в её составе признается наличие некоторых внутренних групп. Разделение совокупности на части происходит под действием какого-либо фактора.
|
|
|
Отношение факториальной дисперсии к остаточной дисперсии при условии, что факториальная дисперсия больше или равна остаточной, называется дисперсионным отношением или критерием Фишера. По его величине соотнесенной с табличным значением судят об эффективности действия фактора (например, фактора А ). В случае, когда остаточная дисперсия больше факториальной, допускается расчет дисперсионного отношения как отношения остаточной дисперсии к факториальной дисперсии.
Порядок проведения занятия
1. Прочитать текст методического обеспечения занятия.
2. Скопировать исходный файл (Лист-1) на следующий лист (Лист-2).
3. Разделить исходную совокупность на 3 – 5 разных по размеру частей.
4. Отметить их разноцветной заливкой и более жирной линией окантовки.
5. Рассчитать «долю», взвешенную по численности объектов в каждой выделенной группе.
6. Проверить правильность расчетов, вычислив сумму долей: должна быть «1».
7. Рассчитать «частоту», взвешенную по численности объектов в каждой выделенной группе.
8. Проверить правильность расчетов, вычислив сумму частот: должна быть «n».
9. Рассчитать «долю», взвешенную по среднему значению диаметра ствола на высоте 1. 3 м для каждой выделенной группе.
10. Проверить правильность расчетов, вычислив сумму долей: должна быть «1».
11. Рассчитать «частоту», взвешенную по среднему значению диаметра ствола на высоте 1, 3 м для каждой выделенной группе.
12. Проверить правильность расчетов, вычислив сумму частот: должна быть «n».
13. Сравнить значения «долей» и «частот» при взвешивании по разным признакам».
14. Самостоятельно выбрать любой другой признак для «взвешивания» и осуществить определение «долей» и «частот», взвешенных по нему.
15. Выбрать два признака для «взвешивания» по их произведению.
16. Повторить работу с большим числом признаков.
17. Выбрать для взвешивания признаки, значимым эффектом взвешивания для которых выступает их сумма, затем их разность, затем их отношение и т. д.
|
|
|
Порядок вычислений. Итоговые величины двухфакторного иерархического дисперсионного анализа вычисляют по общепринятым алгоритмам. Порядок вычисления итоговых величин двухфакторного иерархического дисперсионного анализа рассмотрим на примере анализа двухфакторного иерархического неравномерного (не ортогонального) комплекса. Принципиально, алгоритм расчетов неравномерных комплексов применим и для равномерных комплексов, но не наоборот.
Постановка задачи.
1. Пусть требуется оценить влияние исходных родительских форм на продуктивность гибридов тополей, получаемых для создания промышленных плантаций. Напомним, что тополя относятся к двудомным растениям, т. е. их особи являются разнополыми. Учитываемым признаком будет объем ствола к установленному возрасту (20 лет). Планом гибридизации было предусмотрено использование в качестве отцовских особей 3-х перспективных форм тополя белого, а в качестве материнских – 8 особей тополя Болле. При этом схема скрещивания и количество оставшихся к моменту учета гибридов по каждой комбинации скрещивания будет отражена в таблице 3. 1.
Таблица 3. 1.
Двухфакторный иерархический дисперсионный анализ
| № | Показа-тели | Отцы | Сумма | |||||||
| А1 | А2 | А3 | ||||||||
| Матери | ||||||||||
| В1 | В2 | В3 | В4 | В5 | В6 | В7 | В8 | |||
| 1. | Запас древеси- ны | 1, 0 0, 8 0, 6 0, 8 | 0, 9 0, 7 0, 8 0, 7 0, 5 | 1, 0 1, 1 0, 9 1, 0 | 1, 2 1, 0 1, 0 0, 9 1, 0 1, 1 0, 8 | 0, 9 0, 9 1, 0 0, 8 | 1, 1 1, 2 1, 0 0, 9 1, 0 0, 8 | 1, 0 1, 1 1, 1 0, 8 0, 9 | 0, 9 0, 9 0, 8 1, 1 0, 6 | a=3 b=8 |
| 2. | 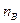
| Σ n=N | ||||||||
| 3. | 
| 3, 2 | 3, 6 | 4, 0 | 7, 0 | 3, 6 | 6, 0 | 4, 9 | 4, 3 | 36, 6 |
| 4. | 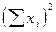
| 10, 24 | 12, 96 | 16, 0 | 49, 0 | 12, 96 | 36, 0 | 24, 01 | 18, 49 | 1339, 56 |
| 5. | 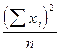
| 2, 56 | 2, 59 | 4, 0 | 7, 0 | 3, 28 | 6, 0 | 4, 80 | 3, 70 | 33, 93 |
| 6. | 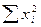
| 2, 64 | 2, 68 | 4, 02 | 7, 10 | 3, 26 | 6, 10 | 4, 87 | 3, 83 | 34, 50 |
| 7. | 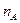
| |||||||||
| 8. | 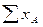
| 6, 8 | 14, 6 | 15, 2 | 36, 6 | |||||
| 9. | 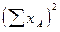
| 46, 24 | 213, 16 | 231, 04 | - | |||||
| 10. | 
| 5, 14 | 14, 21 | 14, 44 | 33, 79 | |||||
Порядок вычислений.
2. Используя материалы первичных наблюдений, приведенные в таблице 3. 1, вычисляем промежуточные вспомогательные величины.
|
|
|
2. 1. Средний квадрат суммы вариант:
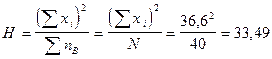 .
.
3. Затем находим суммы квадратов отклонений.
3. 1. Общая сумма квадратов отклонений:
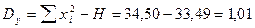 .
.
3. 2. Межгрупповая сумма квадратов отклонений:
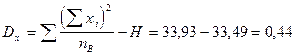 .
.
3. 3. Остаточная сумма квадратов отклонений:
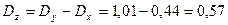 .
.
3. 4. Сумма квадратов отклонений по фактору А:
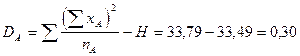 .
.
3. 5. Сумма квадратов отклонений по фактору В:
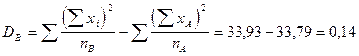 .
.
4. Определяем числа степеней свободы.
4. 1. Общее число степеней свободы (для общей дисперсии):
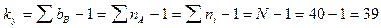 .
.
4. 2. Число степеней свободы по фактору А (для дисперсии по фактору А):
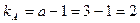 .
.
4. 3. Число степеней свободы по фактору В (для дисперсии по фактору В):
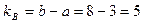 .
.
4. 4. Число степеней свободы по случайным факторам (для остаточной дисперсии):
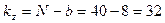 .
.
5. Находим средние квадраты отклонений по факторам, используя полученные величины соответствующих сумм квадратов отклонений и числа степеней свободы.
5. 1. По фактору А – фактору высшего уровня иерархии:
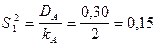
5. 2. По фактору В – фактору низшего уровня иерархии:

5. 3. По остаточной вариации – по случайным факторам – Z:
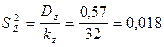
5. 4. Результат записываем в таблицу (табл. 2):
Таблица 3. 2.
|
|
|


