 |
Лабораторная работа № 4. Вводная часть. «Оценка значимости разности между выборочными средними по наименьшей существенной разности (НСР)»
|
|
|
|
Лабораторная работа № 4
Тема лабораторного занятия: «Оценка и анализ значимости различий между объектами отбора, анализ критериев существенности различий»
Ключевые слова: селекция, отбор, эффективность отбора, эффект отбора, наследственность, наследуемость, дисперсионный анализ, наименьшая существенная разность, критерий Тьюки.
Бюджет времени – 4 часа.
Количество двухчасовых занятий – 2.
Распределение бюджета времени:
- 1 час на освоение теоретических основ и принципов определения оценок наименьшей существенной разности и D-критерия Тьюки при проведении массового отбора;
- 1 час на расчеты в электронных таблицах Microsoft Excel оценок наименьшей существенной разности (НСР) в равномерном дисперсионном комплексе;
- 1 час на расчеты в электронных таблицах Microsoft Excel оценок D-критерия Тьюки (D) в равномерном дисперсионном комплексе;
- 1 час на расчеты в электронных таблицах Microsoft Excel оценок наименьшей существенной разности (НСР) и оценок D-критерия Тьюки (D) в неравномерном дисперсионном комплексе;
Дидактический материал, необходимый для проведения данной лабораторной работы, приведен в файлах электронных таблиц Excel – «НСР» (Приложение – 4. 1).
Вводная часть
Важным этапом решения селекционных задач, в частности задач, связанных с отбором, выступает сравнительная оценка результатов селекции между собой (плюсовые деревья по их потомствам при оценке ОКС и СКС, полученные гибриды при их сравнении с эталонным объектом или между собой) и с исходными объектами (популяциями при их сравнительной оценке или отборе особей из них, родителями при гибридизации и т. п. ).
Надежным средством оценки существенности различий между сравнительно изучаемыми объектами лесной селекции выступают критерии существенности различий: наименьшая существенная разность (НСР) и критерий Тьюки (D).
|
|
|
Тема 4. 1.
«Оценка значимости разности между выборочными средними по наименьшей существенной разности (НСР)»
Теоретическая платформа применения оценок наименьшей существенной разности. Критерий НСР устанавливает (определяет) предельную ошибку (критическую величину ошибки) для разности двух выборочных средних, в границах (пределах) которой различия не признаются существенными, и разности (различия между средними) находятся в пределах ошибки опыта. НСР определяется, исходя из следующей формулы:
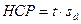 , где
, где
t – критерий Стьюдента (табличное значение для конкретного числа наблюдений и заданного уровня значимости);
sd – ошибка разности средних (вычисляется по материалам дисперсионного анализа, на основе оценки остаточной или средовой дисперсии).
В оценке существенности различий по НСР исходят из того, что в случае, когда фактическая разность между двумя сравниваемыми средними больше или равна НСР, то такая разность признается существенной. Смысл «существенной разности» состоит в том, что разница между выборочными средними, достигающая величины НСР, соответствует разности между такими средними, которые представляют две разные совокупности и не относятся к одной совокупности. Если же фактическая разность между средними величинами меньше НСР, она признается несущественной. В такой ситуации нет оснований рассматривать совокупности, представленные этими средними, как самостоятельные совокупности. Напротив, можно признать то, что рассматриваемые средние принадлежат к единой совокупности.
Порядок вычислений:
1. По данным дисперсионного анализа вычисляют обобщенную ошибку средней:
|
|
|
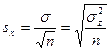
2. Вычисляют ошибку разности средних для неравномерных комплексов:
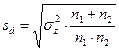 , где
, где
n1 = численность первой из двух сравниваемых совокупностей (выборок, популяций, клонов, пулусибсовых семей и т. п. ), участвующих в дисперсионном анализе;
n2 = численность второй из двух сравниваемых совокупностей;
sd = ошибка разности средних двух совокупностей дисперсионного комплекса;
σ z = остаточная (средовая, случайная) дисперсия (по результатам дисперсионного анализа: в абсолютном смысле дисперсионный анализ в этом случае должен выполняться только для двух сравниваемых совокупностей).
Данный алгоритм используют при парном сравнении значений анализируемых объектов: каждый из объектов сопоставляется с каждым из остальных, в результате чего формируется комплекс значений НСР.
В случае равенства численностей сравниваемых групп формула примет более простой вид:
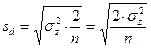 , где
, где
n = численность групп (классов, совокупностей) при реализации равномерной схемы дисперсионного анализа, в которой численности всех групп равны;
sd = средняя ошибка разности средних для всего дисперсионного комплекса (разность двух средних вычисляется при их парном сравнении для всех возможных вариантов сопоставления групп объектов данного дисперсионного комплекса, ошибка вычисляется для всего комплекса в целом).
Вычисленная по данному алгоритму величина sd является общей для всего равномерного дисперсионного комплекса статистикой. Действительно, в формуле её расчета использованы только обобщенные (для всего равномерного дисперсионного комплекса) величины: σ z – остаточная (средовая, случайная) дисперсия; n – численность групп при реализации равномерной схемы. Полученная на её основе величина НСР также будет единой и общей для всего равномерного дисперсионного комплекса. Её значение будет использовано для всех случаев парного сравнения и вычисления разности каждого из объектов дисперсионного комплекса с каждым из других.
В случае неравенства численностей сравниваемых групп (анализ неравномерного дисперсионного комплекса) прибегают к расчету усредненной численности (n). Такой подход позволяет определять величину НСР, обобщенную для всего анализируемого дисперсионного комплекса. Возможность использования такого критерия оценки существенности различий между выборочными средними некоторого (но вполне определенного) дисперсионного комплекса обусловлена тем, что любые вычисления значений НСР в данном комплексе основаны на единой (общей для всех групп) остаточной дисперсии (σ z). Это имеет отношение как к вычислению значений НСР при попарном сопоставлении каждого среднего с каждым из остальных, так и к вычислению общего для комплекса значения НСР.
|
|
|
3. Подставляя значение ошибки разности средних в формулу расчета НСР, получим (в абсолютных и относительных величинах):
НСР05 = t05 × sd HCP05% = 100 × (t05 × sd): Mcp, где
t05 = табличное значение критерия Стьюдента;
sd = средняя ошибка разности средних;
Mc = обобщенное среднее значение признака для всего дисперсионного комплекса.
Следует отметить, что в практических работах чаще используется не процентные, а абсолютное значение НСР, вычисляемое в соответствующих размерных (м, см, кг, г, шт. и т. п. ) или безразмерных величинах (при расчете относительных показателей).
Задание 1. Рассчитайте величину наименьшей существенной разности (НСР) по дидактическому материалу, предложенному преподавателем:
- для равномерного дисперсионного комплекса (файл Excel, лист «Равномерный»: Приложение);
- для неравномерного дисперсионного комплекса (файл Excel, лист «Неравномерный»: Приложение);
Исходным дидактическим материалом для данной работы служит файл Excel «Коэффициент наследуемости» или «НСР» Лист 1 для равномерных дисперсионных комплексов и Лист 3 для неравномерных дисперсионных комплексов. В них для работы используют собственно исходные таблицы данных и перечень вычисляемых промежуточных и итоговых статистик.
Работа предусматривает копирование таблиц в буфер памяти компьютера и перенесение их в новую книгу или на новый лист, используемый для работы студента в первоначальной книге.
Тема 4. 2.
|
|
|


