 |
Теоретическая платформа выполнения работы
|
|
|
|
Теоретическая платформа выполнения работы
Для успешного освоения теоретической платформы выполнения данной лабораторной работы дадим определения используемым понятиям.
Варианса – это мера дисперсии (изменчивости) признака у изучаемых объектов в их совокупности.
Дисперсия – это рассеивание значений признака, разброс значений признака.
Какими бы путями ни создавалась фенотипическая изменчивость в популяциях и из каких бы компонентов она ни состояла, она всегда может быть выявлена и измерена вариансой. Самое существенное заключается в выяснении того, какую долю в общей фенотипической вариансе занимает варианса, зависящая от генетических различий между особями в популяции, то есть установлению величины отношения генотипически обусловленной вариансы к общей фенотипической вариансе. Такое отношение принято называть коэффициентом наследуемости.
Соотношения между значениями генотипической и средовой варианс могут быть различными. Так если экспериментатор работает с клонами (черенковые саженцы, полученные от одного дерева), то в этом случае генотипическая варианса будет равна нулю, и общая фенотипическая варианса будет состоять только из средового компонента. Если же работа ведется на выровненном экофоне (в абсолютно контролируемых условиях фитотронов) с различным по происхождению материалом, то различия между сравниваемыми объектами будут определяться преимущественно (в идеале полностью) различиями в их генотипах.
Коэффициент наследуемости определяется соотношением варианс (дисперсий), поскольку из обычных статистических мер рассеивания (дисперсии) только вариансу (s2 ) можно разложить на компоненты.
|
|
|
С селекционно-генетической точки зрения фенотипическая варианса (оценка степени фенотипического варьирования) в самом простом случае может быть обусловлена тремя причинами:
1. генотипическими различиями, обусловленными непосредственным действием генов (аддитивный компонент вариансы –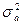 
);
2. генотипическими различиями, возникающими вследствие межаллельных взаимодействий (компонент вариансы, обусловленный доминированием –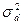 
);
3. ненаследственными различиями между объектами, вызванными неодинаковым влиянием разнообразных локальных проявлений условий среды (компонент вариансы, обусловленный фоновыми условиями внешней среды –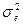 
).
Поскольку компоненты вариансы суммируются, общая фенотипическая варианса (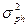 
) представляет их сумму. Общепринята следующая формула её расчета (1):
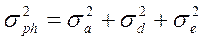(1)
Так как аддитивная генотипическая варианса ( 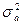)и неаддитивная генотипическая варианса ( 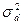) являются генотипическими компонентами фенотипиеческой (общей) изменчивости, то их можно суммировать и получить генотипически обусловленную вариансу ( 
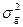), которая формализовано выражается равенством 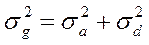(2):
(2)
С учетом этого, общая фенотипическая варианса может быть представлена в следующем виде 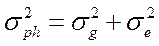(3):
(3)
2. 1. Коэффициент наследуемости в широком смысле, основные понятия
Коэффициент наследуемости в широком смысле – это отношение всей генотипической вариансы к общей фенотипической 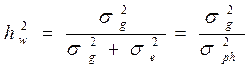(4).
(4)
Этот коэффициент наследуемости является коэффициентом наследуемости в широком смысле (учитывает всю генотипически обусловленную долю наследуемости - и аддитивную и неаддитивную вместе). Он содержит в своем расчетном алгоритме не только стойко наследуемый аддитивный компонент вариансы ( 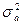), но и компонент, обусловленный эффектом доминирования признаков или неаддитивный компонент вариансы ( 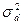), который потомством не наследуется полностью и обусловлен аллельным взаимодействием доминантного и рецессивного генов, находящихся в аллельном состоянии). Это может проявляться и существовать только при наличии в популяциях гетерозиготных генотипов (особей типа – Аа ), что практически всегда наблюдается в популяциях древесных и кустарниковых пород. Гетерозиготные генотипы ( Аа) при строгом отборе расщепляются и образуют гомозиготные генотипы по рецессивным аллелям ( аа ) и по доминантным аллелям ( АА ). Следовательно, не все потомство проявит признаки исходных гетерозиготных особей, то есть наследование признаков исходных родительских форм будет неполным. Поскольку только часть потомства унаследует признаки исходных гетерозиготных родительских форм (в строгом плане – только гетерозиготные особи потомства будут адекватны родителям), то и наследование такого порядка считается неполным. Поэтому коэффициент наследуемости (способности передачи наследственных признаков от родителей к потомкам) в широком смысле дает несколько завышенное значение наследуемости. Тем не менее, он широко применяется при селекционной оценке популяций.
|
|
|
Из формулы расчета (4) видно, что коэффициент наследуемости может варьировать от 0 (в случае полного отсутствия наследования признаков – 
) до 1 (когда отсутствует средовый компонент обусловленности изменчивости и вся она обусловлена генотипически –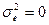 
).
С теоретической точки зрения главное значение коэффициента наследуемости в широком смысле заключается в том, что он дает возможность устанавливать степень надежности суждений о селекционной ценности особей в популяции по их фенотипической ценности (Рокицкий, 1978, стр. 277-279). Фактически же можно непосредственно судить толь о фенотипических ценностях особей, а селекционные ценности определяются по степени их влияния на следующее поколение. Принимая это условие, мы приходим к выводу о том, что селекционер или экспериментатор, используя коэффициент наследуемости в широком смысле, проводит отбор родителей по их фенотипическим ценностям. Успех же отбора в желательном направлении изменения популяции может быть предсказан только в том случае, если известна степень соответствия между фенотипическими и селекционными значениями. Эта степень соответствия определяется коэффициентом наследуемости в узком смысле.
|
|
|
Естественно, что фенотипические и генотипические значения признаков особей не могут оцениваться абсолютно, а оцениваются только как отклонения от популяционной средней (иначе не возможно говорить о селекционной ценности каждого конкретного проявления признака: высота дерева 25 м – это хорошо или плохо? ). Тем не менее, коэффициент наследуемости относится к числу важнейших параметров при генетическом анализе количественных признаков в популяции, его включают почти во все алгоритмы и расчетные формулы, используемые при селекции растений и животных.
Важно иметь в виду, что наследуемость – это не только характеристика признака как такового (разные признаки наследуются в разной степени), но также и популяции, и тех средовых условий, в которых находились особи данной популяции.
Так как коэффициент наследуемости вычисляется на основе ряда величин, то изменение в любой из них повлияет на его значение. При дисперсионном анализе и разложении общей фенотипической изменчивости на составляющие её компоненты мы составляли достаточно развернутое равенство, правая часть которого включала несколько компонентов: аддитивную вариансу, неаддитивную вариансу, средовую вариансу, а в более подробном изложении еще и вариансу взаимодействия факторов и вариансу вызванную наследственными эффектами помимо аддитивности и доминирования. Все генетические компоненты зависят от частот генов, а по ним разные популяции одного вида организмов могут отличаться в силу своей прошлой истории формирования, в силу тех процессов, которые в них происходили. Поэтому неудивительно, что коэффициенты наследуемости по одному и тому же признаку для разных популяций, кажущихся даже очень сходными, бывают неодинаковы.
|
|
|
Так как средовый компонент входит в определение коэффициента наследуемости, то при большой вариации по условиям произрастания (или выращивания) коэффициенты наследуемости будут ниже, а при сравнительно однородных условиях – выше.
Имеют значения и размеры популяций. Если популяция сравнительно мала, то более вероятны в ней процессы гомозиготизации по ряду генов, отсюда сравнительно низкие показатели наследуемости, чем в более крупных по размерам популяциях. Таким образом, обнаруживаемые коэффициенты наследуемости в широком смысле всегда относятся к конкретным популяциям, особи которых находятся в конкретных же условиях произрастания.
ЗАДАНИЕ 1. Рассчитайте величину коэффициента наследуемости в широком смысле при селекционной оценке популяций.
Задание 1 данной лабораторной работы выполняется по дидактическому материалу, представленному в файле электронных таблиц Excel: «Коэффициент наследуемости» (Приложение 2. 1). Варианты дидактического материала для расчета величин достигнутого при отборе селекционного дифференциала и показателя интенсивности отбора как и в предыдущей работе определяются преподавателем или могут быть предложены обучающимся по материалам его собственных исследований.
Общая постановка задачи. Пусть требуется рассчитать величину коэффициента наследуемости в широком смысле для оценки наследуемости (в широком смысле) признаков какого-либо вида древесных или кустарниковых растений по предложенному дидактическому материалу (дидактический материал представлен таблицами исходных данных, файлами электронных таблиц Excel).
Применяемый математический аппарат. Математическим инструментом вычисления коэффициента наследуемости в широком смысле выступает дисперсионный анализ. Особенностью дисперсионного анализа является предоставляемая им возможность разложения общей дисперсии на дисперсию межклассовую (факториальную) и внутриклассовую (остаточную). Напомним, что условиями анализа предусматривается построение дисперсионных комплексов, в каждом из которых содержится некоторое число классов (групп значений), объединяющих некоторое количество значений по принципу принадлежности каждого значения группы только к объектам этой группы и не принадлежность их к объектам любой другой группы (класса). В результате анализа определяют дисперсию признака, обусловленную различиями в классовой принадлежности объектов (различия между классами), и различия, обусловленные случайным варьированием, не вызываемым действием различий между классами (внутриклассовую или остаточную дисперсию). Распределение признаков объектов по классам осуществляется на основе устанавливаемых границ градаций действующего фактора, собственно вызывающего образование различий. Это следует понимать так, что действие какого-либо анализируемого фактора (время, расстояние, наследственная специфика и др. ) приводит к разделению объектов на некоторые группы, отличные друг от друга. В пределах каждой из групп объектов не существует различий, вызываемых действием учитываемого фактора. Тогда имеющаяся неоднородность объектов в пределах какой-либо группы может быть объяснена только случайным варьированием.
|
|
|
Относя все выше сказанное к селекционным проблемам, можно принять следующую прикладную (для решения задач селекционной оценки древесных видов и их популяций) схему дисперсионного анализа.
Схема дисперсионного анализа и условия расчета. Данное задание предусматривает учет и соблюдение ряда условий, которые приведены ниже.
1. Древесные растения и кустарники (оценку ведем в пределах одного вида) размещенные на некоторой (в той или иной степени определенной границами) территории будем рассматривать как популяцию. Происхождение каждого из учитываемых растений семенное, и, следовательно, они различаются, в том числе и генотипически. Принимаем (условно) то обстоятельство, что фенотипические различия между особями будут обусловлены влиянием генотипических различий (влияние аддитивной и неаддитивной составляющих генотипической дисперсии) и влиянием различий в условиях среды (влияние случайной или средовой дисперсии).
2. Различия значений метамерных (повторяющихся) признаков (значения параметров шишек, плодов, семян, листьев, почек, углов крепления ветвей к стволу и т. п. ) в пределах одного растения будут обусловлены только ненаследственными причинами (различиями в условиях освещенности, газообмена, питания и пр. ). Это следует из того обстоятельства, что все образовавшиеся метамерные части и органы растения сформировались под влиянием одного генотипа. Исключение могут составлять семена, образовавшиеся в результате опыления женских генеративных органов одного растения пыльцой различных деревьев. Принципиально такая возможность не исключена. Уровень изменчивости метамерных признаков принимается как уровень изменчивости, обусловленной факторами среды.
3. Тогда возникают предпосылки для оценки каждой из долей общей фенотипической изменчивости.
4. Для таксационных показателей, таких как высота дерева, диаметр ствола, объем ствола, параметры кроны, - имеющих однозначное значение для каждого дерева, указанная схема дисперсионного анализа непригодна. Для таких признаков применение дисперсионного анализа должно предусматривать сравнение нескольких популяций между собой при наличии некоторого разнообразия в пределах популяций.
5. Остановимся на случае, когда анализу подвергаются метамерные признаки особей образующих некоторую популяцию.
Порядок выполнения расчетов. Данное задание предусматривает последовательное решение ряда задач (алгоритм решения приведен ниже).
1. По имеющимся материалам (например, результаты натурных обследований природных популяций: получают у преподавателя) статистического учета одного из метамерных признаков заданного числа растений в популяции (обусловлено заданным уровнем точности и уровнем изменчивости признака в популяции: определяет преподаватель) осуществляют расчет основных описательных статистик и определяют точность опытных данных. В случае достаточного уровня точности (величина относительной ошибки не более 5%) приступают к собственно дисперсионному анализу по предлагаемому ниже алгоритму.
2. Исходные данные группируют в виде комбинационной таблицы таким образом, чтобы градации регулируемого (в нашем случае учитываемого) фактора (в нашем случае – это различия в генетической природе особей) располагались по горизонтали в верхней части таблицы. Обозначим действующий фактор через «А». Тогда в верхней горизонтальной строке таблицы окажутся порядковые номера учетных растений в популяции, соответствующие градациям действующего фактора (каждое растение – самостоятельная градация). Градации фактора «А» образуют столбцы, в которых располагаются варьирующие значения результативного признака (проявление в границах случайной изменчивости формирования признаков в пределах отдельной градации). Их называют вариантами или датами и обозначают «xi». Они группируются по соответствующим градациям организованного (действующего) фактора А (табл. 2. 1).
Таблица 2. 1.
Исходная таблица значений признаков при организации
дисперсионного комплекса (примерный макет составления)
| № п/п |
Номера учетных растений (действующий фактор А): а = 10 |
Сумма | |||||||||
| Признак: (например, длина листовой пластинки, см или диаметр ствола, см и т. д. ) | |||||||||||
| 1. |
| ||||||||||
| 2. | |||||||||||
| 3. | |||||||||||
| 4. | |||||||||||
| 5. | |||||||||||
| 6. | |||||||||||
| 7. | |||||||||||
| 8. | |||||||||||
| 9. | |||||||||||
| 10. | |||||||||||
| ….. | ….. | ||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
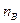
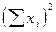
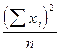
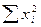
ПримечаниЯ:
- 1. Исходные данные в таблицу 1 заносят из таблиц дидактического материала, которые выдаются каждому студенту преподавателем. Преподаватель определяет: один из анализируемых признаков в каждой из таблиц; количество учетных растений, привлекаемых для анализа; количество учтенных метамеров по каждому из учетных растений.
- 2. Количество столбцов определяется числом учетных растений, включенных в анализ, а количество строк – числом учтенных метамеров.
3. Принимаем основные алгоритмы вычислений в дисперсионном анализе.
3. 1. Общая сумма квадратов отклонений, которая в рабочих алгоритмах чаще используется в виде правой части равенства 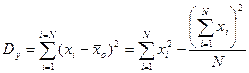(5).
(5)
3. 2. Межгрупповая (факториальная) сумма квадратов отклонений, которая необходима для вычисления значений факториальной дисперсии (6).
(6)
3. 3. Внутригрупповую, или остаточную, сумму квадратов отклонений определяют по разности между общей и межгрупповой суммами квадратов отклонений 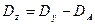(7).
(7)
3. 4. Числа степеней свободы определяем по следующим формулам 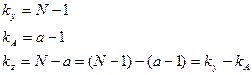(8):
(8)
3. 5. Определяют средние квадраты отклонений или дисперсии: их находят через отношение соответствующих сумм квадратов отклонений к соответствующим степеням свободы 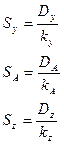(9).
(9)
3. 6. Определяют эффективность действия фактора А (в нашем случае эффективность действия фактора различий между особями) на результирующий признак (в нашем случае на конкретное проявление признака каждой особью). Для этого используют дисперсионное отношение или критерий Фишера F 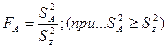(10).
(10)
Так как дисперсионное отношение – величина случайная, его сравнивают с табличным (стандартным) значением.
3. 7. В предложенном алгоритме расчета дисперсионного отношения можно легко увидеть некоторое общее содержание конкретных формул (в расчете общего квадрата отклонений и в расчете факториального квадрата отклонений). Эту общую часть часто выражают знаком « Н » (11) или иным символом.
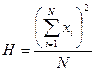(11)
4. Если доказана достоверность влияния действующего фактора, то с помощью дисперсионного анализа можно определить и силу его влияния на результирующий признак. Силу влияния фактора определяют как долю факториальной или межгрупповой изменчивости в общем варьировании признака. Существует ряд способов расчета этого показателя. Наиболее распространенными являются способ Плохинского (1966, 1970) и способ Снедекора (1961).
4. 1. При реализации способа Плохинского исходят из того, что справедливо равенство Dy=Dx+Dz, которое осуществляется в любом дисперсионном комплексе. В этом способе расчета оперируют суммами квадратов отклонений. Делением всех членов этого равенства на Dy получают 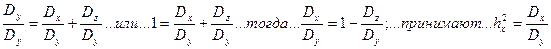(12):
(12)
Показатель h2 принимают как силу влияния действующего фактора, и в ряде случаев его рассматривают как показатель степени наследственной обусловленности различий между особями в популяции или как коэффициент наследуемости в широком смысле. Это справедливо на том основании, что в рассматриваемом примере фактором, вызывающим различия между градациями дисперсионного комплекса, выступает именно разница в генотипах объектов, относимых к разным градациям.
Критерием достоверности этого показателя служит его отношение к своей ошибке, которая вычисляется по следующей приближенной формуле (13):
, где (13)
- a – число градаций фактора А;
- N – общее число вариант: N = Σ ni;
- ni – число вариант в отдельной градации дисперсионного комплекса.
Нулевая гипотеза отвергается, если (14)
(14)
Стандартное значение критерия Фишера берется по таблице. При этом учитывают заданный уровень значимости и число степеней свободы: k1=a-1 (находится в верхней горизонтальной строке таблицы), k2=N-a (находится в первом вертикальном столбце таблицы).
ЗАДАНИЕ к пункту 4. 1. Выполните расчет значений коэффициента наследуемости в широком смысле по методу Плохинского, используя исходный материал, полученный у преподавателя.
4. 2. В способе Снедекора в качестве показателя силы влияния используют отношение дисперсий (средних квадратов отклонений), а именно межгрупповой дисперсии к общей дисперсии для всего комплекса, которая определяется как сумма дисперсий межгрупповой и остаточной (15):
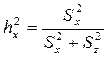. (15)
При этом межгрупповая дисперсия определяется с учетом влияния на групповые характеристики комплекса случайных нерегулируемых факторов (исходя из тезиса: различия между особями обусловлены не только влиянием собственно различиями в их происхождении, но и различиями в условиях произрастания каждого из них). Расчет факториальной дисперсии в этом случае ведут по формуле (16):
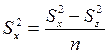, где (16)
- 
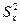– факториальная дисперсия, без учета дисперсии, вызванной влиянием среды;
- 
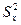– межгрупповой средний квадрат отклонений или «неисправленная» межгрупповая дисперсия;
- 
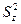– остаточная дисперсия;
- 
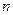– численность вариант в отдельных группах (градациях действующего фактора) дисперсионного комплекса при равенстве численностей внутри всех градаций.
Если числа вариант в градациях комплекса неодинаковы (неравномерный дисперсионный комплекс), то величина n определяется по формуле (17):
, где (17)
- 
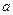– число градаций фактора А (в расчетах по нашему примеру – это число особей в выборке);
- 
– число наблюдений в дисперсионном комплексе;
- 
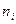- число наблюдений в пределах каждой из градаций фактора А;
- i = 1…a – порядковый номер градации.
Тогда показатель силы влияния фактора приобретает следующее выражение 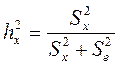(18):
(18)
Достоверность показателя силы влияния фактора, определяемого по методу Снедекора, устанавливается обычным в дисперсионном анализе способом (19),
, (19)
т. е. посредством дисперсионного отношения (критерия Фишера), величина которого сравнивается с критическим табличным значением для принятого уровня значимости и чисел степеней свободы kx = а-1и kz=N-a.
ЗАДАНИЕ к пункту 4. 2. Выполните расчет значений коэффициента наследуемости в широком смысле по методу Снедекора, используя исходный материал, полученный у преподавателя. Вместе с тем следует помнить, что, данный метод расчета имеет свои ограничения. В частности, в ситуации, когда величина случайной дисперсии велика на столько, что превышает значения факториальной дисперсии ( 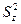≥ 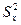), значения коэффициента наследуемости принимают отрицательное значение, а в случае их равенства принимают нулевое значение.
2. 2. Вычисление значений коэффициента наследуемости в узком смысле
Наследуемость в узком смысле, или как её часто обозначают – действительная или аддитивная наследуемость, оценивается коэффициентом наследуемости в узком смысле. Коэффициент наследуемости в узком смысле показывает отношение аддитивной вариансы к общей фенотипической вариансе. Его рекомендуют рассчитывать по следующей формуле (20):
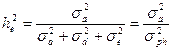где: (20)
- σ 2a – варианса, обусловленная собственно аддитивной наследуемостью (аддитивная варианса);
- σ 2d – варианса, обусловленная эффектом доминирования;
- σ 2e – варианса, обусловленная влиянием случайных факторов (средовая варианса);
- σ 2ph – общая варианса (фенотипическая варианса).
|
|
|
