 |
ПРИМЕР 2. (реконструкция по М.М. Котову, 1997 с необходимой коррекцией и дополнениями).
|
|
|
|
ПРИМЕР 2. (реконструкция по М. М. Котову, 1997 с необходимой коррекцией и дополнениями).
Пусть требуется оценить общую и специфическую комбинационную способность родительских деревьев дуба черешчатого по высоте 20-летнего потомства, полученного от односторонних прямых диаллельных скрещиваний. Исходные данные приведены в таблице 6. 7.
Расчет ведется по схеме равномерного (ортогонального) дисперсионного двухфакторного комплекса при независимых факторах. Результаты учета и их первичной обработки приведены в таблице.
Таблица 6. 7.
Высота гибридов плюсовых деревьев дуба (в возрасте 20 лет)
| № варианта | Комбинация скрещивания | Повторности | Учетные растения | |||||||||
| 1 × 2 | 5, 5 | 5, 4 | 6, 0 | 6, 2 | 6, 1 | 6, 4 | 6, 1 | 6, 0 | 5, 9 | 6, 0 | ||
| 5, 9 | 6, 1 | 6, 1 | 6, 3 | 5, 8 | 5, 7 | 5, 1 | 6, 4 | 6, 0 | 6, 1 | |||
| 6, 4 | 6, 0 | 6, 2 | 5, 8 | 5, 9 | 5, 7 | 5, 0 | 6, 0 | 6, 2 | 6, 3 | |||
| 1х3 | 6, 5 | 6, 5 | 6, 1 | 5, 5 | 5, 4 | 4, 9 | 6, 1 | 6, 3 | 6, 4 | 6, 3 | ||
| 6, 0 | 5, 9 | 5, 8 | 6, 3 | 6, 5 | 5, 2 | 6, 3 | 6, 2 | 6, 1 | 6, 1 | |||
| 6, 3 | 6, 1 | 5, 4 | 5, 0 | 6, 5 | 6, 3 | 6, 0 | 5, 9 | 5, 8 | 5, 6 | |||
| 1х4 | 3, 0 | 3, 4 | 2, 8 | 3, 2 | 3, 0 | 3, 0 | 2, 9 | 2, 8 | 3, 6 | 3, 4 | ||
| 3, 5 | 3, 4 | 3, 4 | 3, 2 | 2, 8 | 2, 8 | 2, 0 | 4, 1 | 4, 1 | 2, 1 | |||
| 4, 0 | 4, 1 | 3, 2 | 3, 1 | 2, 5 | 2, 5 | 3, 8 | 2, 1 | 3, 0 | 3, 1 | |||
| 2х3 | 3, 1 | 3, 0 | 2, 8 | 2, 6 | 3, 4 | 3, 0 | 2, 5 | 2, 1 | 2, 9 | 3, 1 | ||
| 4, 1 | 3, 0 | 3, 6 | 3, 4 | 2, 8 | 2, 8 | 2, 9 | 3, 1 | 3, 2 | 3, 4 | |||
| 3, 9 | 3, 9 | 3, 6 | 3, 5 | 3, 5 | 2, 5 | 3, 4 | 3, 8 | 4, 0 | 4, 0 | |||
| 2х4 | 2, 5 | 4, 1 | 4, 1 | 3, 9 | 3, 5 | 3, 5 | 3, 9 | 4, 0 | 4, 9 | 2, 6 | ||
| 4, 1 | 2, 6 | 4, 1 | 3, 9 | 3, 6 | 3, 8 | 3, 8 | 4, 1 | 3, 6 | 3, 8 | |||
| 4, 0 | 4, 1 | 4, 1 | 4, 0 | 4, 9 | 3, 9 | 3, 9 | 3, 8 | 3, 5 | 3, 5 | |||
| 3х4 | 3, 5 | 3, 5 | 3, 8 | 3, 5 | 2, 8 | 4, 1 | 4, 1 | 4, 0 | 2, 9 | 3, 9 | ||
| 4, 1 | 4, 0 | 4, 0 | 4, 1 | 4, 0 | 3, 9 | 3, 9 | 3, 2 | 3, 1 | 2, 9 | |||
| 2, 8 | 2, 9 | 4, 9 | 4, 1 | 4, 0 | 3, 8 | 3, 8 | 3, 8 | 3, 4 | 3, 0 | |||
Примечание. Принципиально возможно добавить информацию о дисперсионном анализе – базовая модель, двухфакторная модель.
|
|
|
Для дальнейших расчетов полезно сформировать таблицу значений степеней свободы для каждого источника изменчивости и численностей градаций каждого из организованных факторов (табл. 6. 7).
Таблица 6. 7.
Числа степеней свободы для разных источников варьирования
| общая | ky = a × r × n – 1 | ky = 6× 3× 10 – 1 = | = 179 |
| гибриды | ka = a – 1 | ka = 6 – 1 = | = 5 |
| повторности | kr = r – 1 | kr = 3 – 1 = | = 2 |
| Взаимодействие гибридов и повторностей | kar = (a – 1) × (r – 1) | kar = (6 – 1)× (3 – 1) = | = 10 |
| Остаток или ошибка, или случайная дисперсия | kz = ky – ka – kr – kar = (a × r × n – 1) – (a – 1) – (r – 1) – ((a – 1) × (r – 1)) = a× r× n – 1 – a + 1 – r + 1 – (a× r – r – a + 1) = a× r× n – a – r + 1 – a× r + r + a – 1 = a× r× n – a× r = a× r× (n – 1) или, что тоже самое kz = N – a × r = a× r× n – a × r = a× r× (n – 1) | ||
| OKC | kOKC = p – 1 | kOKC = 4 – 1 = | |
| CKC | kCKC = [p × (p – 3)]/2 | kCKC = [4× (4 – 3)]/2 = |
В таблице при определении числа степеней свободы остаточной или средовой или случайной или экотипической изменчивости исходим из представления о числе степеней свободы остаточной дисперсии как о разности между общим числом степеней свободы и степенями свободы всех организованных факторов (Гужов, Фукс, Валичек, 1991, стр. 334; Доспехов, 1973, стр. 167 – 168; Лакин, 1980, стр. 219, 221, 233), а именно (25):
a× b× (c – 1)× b× c = (a× b× c – a× b) × b× c = (25)
Тогда получим (26):
= (a – 1) × (r – 1) × n = (a× r – r – a +1) × n = a× r× n – r× n – a× n + n = a× r× n – (r× n + a× n) + n = a× r× n – n× (r + a) + n = a× r× n – n× (r + a) – 1. (26)
Исходные данные и начальные этапы проведения двухфакторного неиерархического дисперсионного анализ семенного потомства плюсовых деревьев дуба черешчатого представлены в таблице 6. 8.
|
|
|
Таблица 6. 8.
Дисперсионный анализ высоты 20-летних гибридов дуба
| Крите- рии | Варианты опыта - Гибридные комбинации (а) а=6 | Сумма | ||||||||||||||||||
| а1 (1х2) | а2 (1х3) | а3 (1х4) | а4 (2х3) | а5 (2х4) | а6 (3х4) | |||||||||||||||
| Повторности испытания потомства (r=3) в каждой комбинации скрещивания Фактор низшей иерархии |
| |||||||||||||||||||
|
| ||||||||||||||||||||
| Hi | 5, 5 | 5, 9 | 6, 4 | 6, 5 | 6, 0 | 6, 3 | 3, 0 | 3, 5 | 4, 0 | 3, 1 | 4, 1 | 3, 9 | 2, 5 | 4, 1 | 4, 0 | 3, 5 | 4, 1 | 2, 8 |
| |
| 5, 4 | 6, 1 | 6, 0 | 6, 5 | 5, 9 | 6, 1 | 3, 4 | 3, 4 | 4, 1 | 3, 0 | 3, 0 | 3, 9 | 4, 1 | 2, 6 | 4, 1 | 3, 5 | 4, 0 | 2, 9 | |||
| 6, 0 | 6, 1 | 6, 2 | 6, 1 | 5, 8 | 5, 4 | 2, 8 | 3, 4 | 3, 2 | 2, 8 | 3, 6 | 3, 6 | 4, 1 | 4, 1 | 4, 1 | 3, 8 | 4, 0 | 4, 9 |
| ||
| 6, 2 | 6, 3 | 5, 8 | 5, 5 | 6, 3 | 5, 0 | 3, 2 | 3, 2 | 3, 1 | 2, 6 | 3, 4 | 3, 5 | 3, 9 | 3, 9 | 4, 0 | 3, 5 | 4, 1 | 4, 1 |
| ||
| 6, 1 | 5, 8 | 5, 9 | 5, 4 | 6, 5 | 6, 5 | 3, 0 | 2, 8 | 2, 5 | 3, 4 | 2, 8 | 3, 5 | 3, 5 | 3, 6 | 4, 9 | 2, 8 | 4, 0 | 4, 0 | |||
| 6, 4 | 5, 7 | 5, 7 | 4, 9 | 5, 2 | 6, 3 | 3, 0 | 2, 8 | 2, 5 | 3, 0 | 2, 8 | 2, 5 | 3, 5 | 3, 8 | 3, 9 | 4, 1 | 3, 9 | 3, 8 | |||
| 6, 1 | 5, 1 | 5, 0 | 6, 1 | 6, 3 | 6, 0 | 2, 9 | 2, 0 | 3, 8 | 2, 5 | 2, 9 | 3, 4 | 3, 9 | 3, 8 | 3, 9 | 4, 1 | 3, 9 | 3, 8 | |||
| 6, 0 | 6, 4 | 6, 0 | 6, 3 | 6, 2 | 5, 9 | 2, 8 | 4, 1 | 2, 1 | 2, 1 | 3, 1 | 3, 8 | 4, 0 | 4, 1 | 3, 8 | 4, 0 | 3, 2 | 3, 8 | |||
| 5, 9 | 6, 0 | 6, 2 | 6, 4 | 6, 1 | 5, 8 | 3, 6 | 4, 1 | 3, 0 | 2, 9 | 3, 2 | 4, 0 | 4, 9 | 3, 6 | 3, 5 | 2, 9 | 3, 1 | 3, 4 | |||
| 6, 0 | 6, 1 | 6, 3 | 6, 3 | 6, 1 | 5, 6 | 3, 4 | 2, 1 | 3, 1 | 3, 1 | 3, 4 | 4, 0 | 2, 6 | 3, 8 | 3, 5 | 3, 9 | 2, 9 | 3, 0 | |||

| N=180 | |||||||||||||||||||
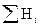
| 59, 6 | 59, 5 | 59, 5 | 60, 0 | 60, 4 | 59, 0 | 36, 1 | 37, 2 | 36, 5 | Σ Σ Hi= 772, 6 | ||||||||||
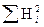
| 356, 04 | 355, 23 | 355, 47 | 362, 48 | 365, 98 | 348, 81 | 132, 27 | 140, 30 | 136, 95 | Σ Σ H2i=3615, 81 | ||||||||||

| 355, 22 | 354, 02 | 354, 02 | 360, 00 | 364, 82 | 348, 10 | 130, 32 | 138, 38 | 133, 22 | (Σ Hi)2 Σ -------- ni 3595, 60 | ||||||||||
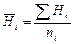
| 5, 96 | 5, 95 | 5, 95 | 6, 00 | 6, 04 | 5, 90 | 3, 61 | 3, 72 | 3, 65 | Σ Hi Σ -------- ni = 77, 51 | ||||||||||
Решение задачи состоит из трех этапов:
1. доказательство существенности различий между гибридными комбинациями;
|
|
|
2. доказательство наличия эффектов комбинационной способности;
3. анализа комбинационной способности отдельных родителей и вариантов скрещивания.
1 этап.
Различия между гибридными комбинациями оцениваются по F критерию Фишера в двухфакторном дисперсионном комплексе (табл. 6. 8).
1. Вычисляем общую сумму квадратов отклонений:
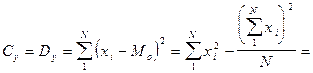
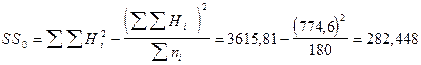 .
. 
2. На следующем этапе находим межгрупповой квадрат отклонений – общий факториальный квадрат отклонений:
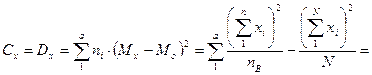
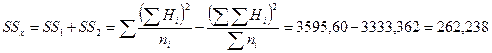
Здесь величина Н вычисляется по нижеприведенной формуле:
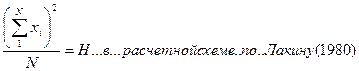
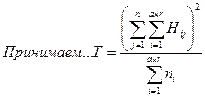
3. Далее находим вспомогательную промежуточную величину – сумму взвешенных квадратов сумм по фактору А (по отношению к числу вариант в пределах каждой соответствующей градации фактора А) для расчета суммы квадратов отклонений по фактору А:

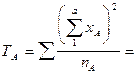
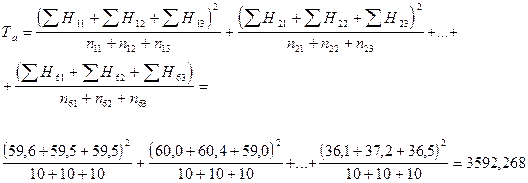
4. После этого определяем сумму квадратов отклонений по первому фактору – фактору высшего уровня иерархии (фактору А):
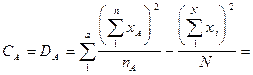
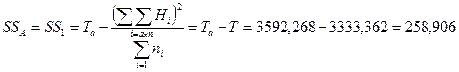
5. Рассчитываем остаточную сумму квадратов отклонений (по неорганизованным факторам), используя представление об остаточной дисперсии как о той доле её общей величины, которая представляет собой разность между общей дисперсией и дисперсией всех организованных факторов:
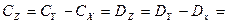
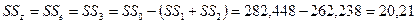
6. На следующем этапе вычисляем вариансы или средние квадраты отклонений: вариансу по первому фактору – различия между гибридными комбинациями (А) – ms1 и остаточную вариансу – по неорганизованным факторам (Z) – ms3:
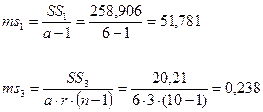

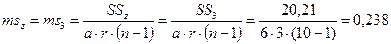
7. В заключении находим критерий Фишера:
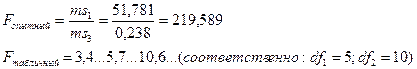
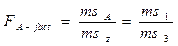
Сравнение фактического значения критерия Фишера с его табличным значением (на трех уровнях значимости) показывает наличие существенных различий между гибридными комбинациями.
|
|
|


