Вводная часть. Теоретическая платформа выполнения работы

Вводная часть

Объекты лесной селекции (плюсовые деревья, элитные деревья, плюсовые насаждения, гибриды и т. п. ) могут быть охарактеризованы некоторым набором параметров (высота дерева, диаметр ствола, протяженность бессучковой зоны ствола и т. д. ). Каждый из них рассматривается как многопараметрический объект, подлежащий многостороннему описанию (описанию по всему комплексу признаков, свойственных ему). Их сравнительная селекционная оценка требует привлечения современных методов многомерного анализа, к числу которых относят определение евклидовой дистанции и выполнение на этой основе кластерного анализа с построением дендрограмм.

Одной из проблем современных биологических, сельскохозяйственных и лесоводственных исследований является обеспечение комплексности оценок степени близости или отдаленности сравниваемых объектов. Вполне актуальна комплексная оценка генетической близости сравниваемых популяций, экотипов, плюсовых деревьев или их клоновых групп, форм и сортов растений, пород или типов животных. Сказанное в полной мере относится к любым биологическим, сельскохозяйственным или лесоводственным объектам вообще.

 

ПРИМЕР.

1. Отдельное дерево обладает такими характеристиками как высота, диаметр ствола, протяженность бессучковой зоны ствола, диаметр проекции кроны, площадь поперечного сечения ствола, объем стволовой древесины и многими другими.

2. Каждая шишка на дереве (например, у сосны обыкновенной) также обладает целым набором характеристик. Часть из них устанавливается в процессе непосредственного учета параметров (масса, длина, максимальный диаметр, боковое расстояние от вершины до плоскости максимального диаметра). Другие определяются в результате преобразования первых.

 

Теоретическая платформа выполнения работы

Теоретической основой метода выступает представление о каждом конкретном объекте как о некой «точке», помещенной во вполне конкретное место многомерного пространства (поля или, если хотите, информационного поля), каждая координатная ось которого соответствует одному из признаков в системе признаков, используемых для анализа. При этом каждая характеристика объекта (каждое проявление каждого из его признаков) рассматривается как соответствующая количественная величина одного из многочисленных (по количеству мерности многомерного пространства) векторов. Иными словами, местоположение «точки» в многомерном пространстве определяется многочисленными координатами (по количеству мерности многомерного пространства), выраженными в количественном виде. В свою очередь расстояние между объектами в таком многомерном пространстве есть обобщенная разница в их координатах. Для наглядности и детализации представления о таком подходе к организации исследований рассмотрим ряд очевидных (понимаемых однозначно) позиций или примеров.

Для ответа на вопрос о степени близости или отдаленности сравниваемых между собой многопараметрических объектов предусматривается решение идентификационных и классификационных задач. Достаточно широко распространенным на современном этапе и наиболее эффективным средством решения подобных задач выступают методы комплексного анализа, в частности факторный и кластерный анализ (Харман, 1972; Окунь, 1974; Лейтас, 1983; Бессчетнова, 2004б, в, г; 2013 в; 2014в; Семихов, 2007б; Maltamo, 2001; Sironen, 2001; Temesgen, 2008; Kesari, 2010; Androsiuk, 2011).

Одной из форм реализации такого анализа является определение обобщенного статистического расстояния в многомерном пространстве признаков, в частности евклидова расстояния, линейного расстояния, расстояния Махаланобиса (Никитин, 1978; Песенко, 1982; Лейтас, 1983; Мандель, 1988; Мэйндональд, 1988; Марущак, 1991; Kaushik, 2007). Оно позволяет выявить дивергенцию и генотипические различия объектов по комплексу признаков, исключая изменчивость под воздействием окружающей среды (Кукеков, 1978; Петров, 1984; Tausz, 2001). Сравнив полученные оценки, удается сделать заключение о том, какие из многопараметрических объектов, размещенных в едином многомерном пространстве, наиболее близки между собой, а какие – отдалены друг от друга по всему комплексу анализируемых признаков.

Важной теоретической позицией факторного или кластерного анализа принимается условие о том, что признаков, по которым выполняют эти многомерные анализы, может быть неограниченное количество (на современном этапе развития теоретических положений метода это не определено), но при этом все объекты должны характеризоваться одним и тем же набором параметров (признаков), т. е. должны располагаться в едином многомерном пространстве, каждая точка которого характеризуется (описывается, определяется) одним и тем же набором координат. Значение признака может быть равным «нулю», когда проявление признака отсутствует (количество колючек на единице длины побега у неколючих особей или плотность волосков на единице площади листовой пластинки при отсутствии опушенности и т. п. ). В этом случае координата признака (величина или длина соответствующего вектора) равна «нулю», но сам признак не отсутствует в системе отсчета как координатный элемент. Это условие является одним из основных условий проведения такого анализа.

В контексте вышесказанного необходимо обеспечить наличие одинакового набора анализируемых признаков у каждого из объектов многомерного комплекса сравнения. Лесоводственнные объекты (насаждения, отдельные плюсовые деревья или их клоны), не имеющие (по той или иной причине), хотя бы одной из характеристик, должны исключаться из схемы опыта (Булыгин, 1978, Никитин, 1978; Лейтас, 1983; Петров, 1984; Марущак, 1991; Насонов, 1996; Бессчетнова, 2006; 2011; 2014; 2015). Организация комплекса должна предусматривать такой подход, при котором каждый многомерный объект описывался однозначными оценками учитываемых параметров, каждая из которых имела отношение только к данному объекту (насаждению, лесничеству, плюсовому дереву и т. д). То есть каждый из объектов в ходе первичного изучения получает некоторый, но одинаковый для всех объектов, набор количественных характеристик, число которых определяет мерность собственно многомерного пространства признаков. Следовательно, принципом формирования числовых массивов должно явиться то, что относительно каждого из признаков существует возможность вычисления оценок корреляции и ковариации со всеми остальными признаками объектов в многомерном комплексе сравнения. Вычисление на этих условиях обобщенных расстояний между объектами в многомерном пространстве признаков позволяет дать для комплекса анализируемых объектов сопоставимые оценки того, насколько близко или отдаленно друг от друга объекты расположены в заданном для анализа многомерном пространстве. При выборе признаков для многомерного анализа следует исходить из того, что объекты, их носители, должны иметь некоторую принципиальную общность и системность характеристик (принадлежность к одному биологическому виду или к одинаковой селекционной категории, размещение на одном лесном участке, одинаковый возраст, одинаковую степень развития учитываемых метамеров и т. п. ).

 

Порядок проведения занятия.

18. Прочитать текст.

19. Скопировать исходный файл (Лист-1) на следующий лист (Лист-2).

20. Вычислить средние значения и величины среднего квадратического отклонения по каждому признаку, используя встроенные функции Excel.

21. Используя полученные величины и матрицу исходных значений признаков, вычислить нормированные значения каждого признака для каждого из объектов и сформировать из них матрицу нормированных значений.

22. Проверить правильность расчетов, вычислив среднее значение нормированных признаков и их общую дисперсию и среднее квадратическое отклонение: среднее значение должно быть равно «0», а СКО – «1».

23. Последовательно рассчитать разности нормированных значений соответствующих признаков двух сравниваемых селекционных объектов (двух плюсовых деревьев).

24. Вычислить квадраты полученных разностей нормированных значений и внести их в соответствующую строку рабочей таблицы Excel.

25. Рассчитать обобщенное статистическое расстояние для данной пары объектов и записать его значение в таблицу на листе 3. Использовать непосредственную запись или копирование с использованием функции «Специальная вставка» - «Вставить значение». Функцию «Вставить связь» в этом алгоритме расчета не использовать!

26. Продолжить вычисления указанных величин для следующей пары сравниваемых многомерных объектов.

27. Используя шаблоны расчетных таблиц (Лист 4), сформировать таблицу исходных данных, содержащую информацию об «эталонном объекте». Эталонный объект представляется как «абстракция идеализации» - абстрактное плюсовое дерево, характеристики которого соответствуют «лучшим» значениям соответствующих признаков в комплексе сравниваемых между собой реальных плюсовых деревьев (любых объектов селекции).

28. Вычислить средние значения и величины среднеквадратического отклонения по каждому признаку, используя встроенные функции Excel, для матрицы исходных значений с учетом наличия в её составе «эталонного объекта».

29. Произвести процедуру нормирования исходных значений и вычислить обобщенное статистическое расстояние каждого из реальных объектов от «эталонного объекта».

 

Техника применения метода. Матрица средних значений (табл. 1) представлена размерными и безразмерными неравнозначными и разно-размерными величинами, характеризующими объект (популяцию, экотип и т. п. ), например: длина или ширина листовой пластинки – в сантиметрах, масса плода (или шишки) – в граммах или миллиграммах, площадь листовой пластинки или площадь поперечного сечения ствола – в сантиметрах квадратных, коэффициент формы плода или листовой пластинки у цветковых растений – в безразмерных величинах, коэффициент формы шишки у хвойных – в безразмерных величинах.

 

ПРИМЕР. Примером такой матрицы исходных размерных и неоднородных значений может служить таблица средних значений признаков у особей различных популяций облепихи крушиновидной (табл. 1), полученные в ходе селекционной инвентаризации природных популяций этого растения.

 

Особенностью метода является возможность использования в расчетах статистических комплексов, представленных только однородными величинами, что наиболее удобно представлять в форме безразмерных величин. Для этой цели матрица исходных данных преобразуется в матрицу нормированных значений (табл. 2).

При этом все они (нормированные значения) являются безразмерными, их распределение обеспечивает нулевое среднее значение (среднее значение всех нормированных величин в пределах каждого признака в сумме даст «ноль»), а среднеквадратическое отклонение равно единице (учитывается среднеквадратическое отклонение каждого из средних, введенных в комплекс сравнения, от обобщенного среднего).

 

ПРИМЕР. Примером матрицы нормированных значений может явиться таблица нормированных значений признаков популяций облепихи (табл. 2).

 

Таблица 1.

Средние значения признаков популяций облепихи (исходная матрица)

№ п. п.	Популяции в поймах рек и в прибрежных зонах озер	Длина плодо-ножки, мм	Диаметр плода, мм	Длина плода, мм	Масса плода, г	Длина листа, см	Ширина листа, мм	Коэф-фициент формы плода	Коэф-фициент формы листа	Коэф-фициет площади листа	Коли-чество колючек, шт. /дм
1.	Бес-Агач	4, 278	5, 123	5, 950	0, 082	4, 601	3, 983	1, 175	1, 195	1, 349	2, 555
2.	Каркара	2, 545	6, 996	7, 353	0, 214	5, 026	5, 959	1, 054	0, 873	3, 006	2, 128
3.	Каинды	3, 550	5, 517	6, 291	0, 113	5, 205	4, 672	1, 150	1, 153	2, 437
4.	Чилик	4, 163	5, 914	6, 738	0, 133	5, 340	4, 867	1, 146	1, 120	2, 604	2, 366
5.	Кульсай	4, 287	6, 037	6, 578	0, 145	4, 991	4, 613	1, 090	1, 101	2, 346	3, 162
6.	Большая Алма-Атинка	3, 359	6, 429	6, 634	0, 170	6, 254	6, 284	1, 031	1, 009	3, 958	1, 887
7.	Чу	4, 093	5, 523	5, 777	0, 113	4, 441	4, 573	1, 051	0, 998	2, 048	4, 385
8.	Усек	4, 632	6, 098	7, 056	0, 162	6, 725	5, 078	1, 158	1, 337	3, 432	1, 266
9.	Каратал	4, 638	6, 388	7, 641	0, 189	4, 888	4, 993	1, 199	0, 997	2, 501	1, 892
10.	Лепсы	4, 446	6, 459	7, 325	0, 188	5, 160	5, 332	1, 138	0, 977	2, 788	1, 801
11.	Аксай	4, 251	6, 144	6, 768	0, 181	5, 906	5, 336	1, 109	1, 117	3, 211	2, 443
12.	Бель-Булак	3, 562	5, 691	6, 468	0, 146	5, 568	4, 809	1, 138	1, 161	2, 739	2, 113
13.	Баян-Кол	3, 288	5, 943	6, 581	0, 167	5, 605	4, 927	1, 112	1, 183	2, 757	1, 783
14.	Тасты-Булак	3, 617	5, 757	6, 592	0, 124	5, 538	5, 005	1, 157	1, 146	2, 813	1, 538
15.	Зайсан	5, 425	7, 291	10, 068	0, 359	6, 992	7, 175	1, 408	1, 004	5, 060	1, 844

 

 

Таблица 2.

Нормированные значения признаков популяций облепихи (матрица нормированных значений)

№ п. п.	Популяции в поймах рек и в прибрежных зонах озер	Длина плодо-ножки	Диаметр плода	Длина плода	Масса плода	Длина листа	Ширина листа	Коэф-фициент формы плода	Коэф-фициент формы листа	Коэф-фициет площади листа	Коли-чество колючек
1.	Бес-Агач	0, 310	-1, 235	-1, 006	-1, 310	-0, 980	-1, 186	0, 251	0, 466	-1, 181	0, 255
2.	Каркара	-1, 583	1, 181	0, 456	0, 777	-0, 499	0, 825	-0, 649	-1, 017	0, 147	-0, 053
3.	Каинды	-0, 419	-0, 727	-0, 651	-0, 826	-0, 297	-0, 484	0, 060	0, 273	-0, 507	-0, 151
4.	Чилик	0, 176	-0, 216	-0, 186	-0, 497	-0, 144	-0, 286	0, 033	0, 120	-0, 315	0, 119
5.	Кульсай	0, 310	-0, 057	-0, 353	-0, 323	-0, 538	-0, 545	-0, 384	0, 031	-0, 612	0, 692
6.	Большая Алма-Атинка	-0, 698	0, 448	-0, 295	-0, 084	0, 888	1, 156	-0, 821	-0, 391	1, 238	-0, 226
7.	Чу	0, 099	-0, 720	-1, 186	-0, 828	-1, 160	-0, 586	-0, 675	-0, 442	-0, 953	-1, 573
8.	Усек	0, 686	0, 022	0, 144	0, 045	1, 420	-0, 072	0, 124	1, 117	0, 635	-0, 673
9.	Каратал	0, 692	0, 392	0, 753	0, 374	-0, 656	-0, 158	0, 425	-0, 445	-0, 433	-0, 222
10.	Лепсы	0, 484	0, 487	0, 424	0, 358	-0, 347	0, 187	-0, 028	-0, 538	-0, 104	-0, 288
11.	Аксай	0, 271	0, 081	-0, 155	0, 260	0, 495	0, 191	-0, 245	0, 108	0, 382	0, 177
12.	Бель-Булак	-0, 477	-0, 495	-0, 467	-0, 305	0, 113	-0, 345	-0, 026	0, 308	-0, 160	-0, 063
13.	Баян-Кол	-0, 776	-0, 178	-0, 350	0, 034	0, 155	-0, 225	-0, 223	0, 408	-0, 139	-0, 301
14.	Тасты-Булак	-0, 417	-0, 418	-0, 339	-0, 646	0, 079	-0, 146	0, 113	0, 240	-0, 076	-0, 477
15.	Зайсан	1, 548	1, 561	3, 279	3, 059	1, 643	2, 064	1, 978	-0, 415	2, 504	-0, 257

 

 

Нормирование производится путем следующего преобразования каждого исходного значения, включенного в исходную матрицу.

1. Разница между каждым исходным значением признака и его обобщенным средним значением делится на обобщенное среднеквадратическое отклонение. Здесь каждое исходное значение признака – это среднее его значение для популяции (или экотипа, или плюсового дерева, представленного клонами и т. п. ), полученное в результате статистической обработки исходного фактического материала, полученного на объекте (в популяции, в пределах сорта или экотипа и т. д. ) в ходе биометрирования учетных растений, составляющих выборку. Обобщенное среднее значение получается в результате математической обработки всего обобщенного цифрового массива, представляющего совокупность всех частных (в пределах популяции, сорта, экотипа и т. п. ) выборок. Обобщенное среднеквадратическое отклонение высчитывается в ходе статистической обработки обобщенной выборки (обобщенного цифрового массива, включающего в себя все частные выборки по популяциям или экотипам). Следовательно, обобщенный статистический анализ дает две статистики (две величины), используемые для нормирования: обобщенное среднее значение по каждому признаку и обобщенное среднеквадратическое отклонение по каждому признаку.

2. Для расчета обобщенного среднего значения каждого признака и обобщенного среднеквадратического отклонения по нему формируется обобщенная выборка – обобщенный цифровой массив из результатов замеров признака на всех учетных растениях (клонах плюсового дерева, учетных площадках и т. п. ) во всех популяциях или экотипах (или сортах, формах, плюсовых деревьях и т. п. ). Обработка ведется по каждому признаку отдельно.

3. Кроме этого предусматривается статистическая обработка данных в пределах каждой популяции (экотипа, сорта и т. д. ) с расчетом популяционных средних (и всех необходимых статистик). Для этого применяются такие же программы статистических расчетов, ориентированные на объем выборки в пределах отдельного объекта в комплексе сравниваемых объектов (популяции, сорта, экотипа и т. п. ).

4. Полученные в ходе этих (и на популяционном уровне, и на обобщенном уровне) расчетов данные (популяционные средние, обобщенные средние, обобщенные среднеквадратические отклонения по каждому признаку) используются для получения нормированных безразмерных однородных значений. Для этого применяется формула (1):

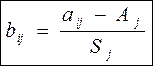, где:                                                                         (1)

- i = 1, … n – индекс значения (порядковый номер) объекта, (популяции, экотипа или т. п. );

- j = 1, …k – индекс значения (порядковый номер) анализируемого признака;

- b_ij – элемент матрицы нормированных значений;

- a_ij – элемент матрицы исходных значений;

- A_j – обобщенное среднее значение j-го признака;

- S_j – обобщенное среднеквадратическое отклонение j-го признака;

- n – количество сравниваемых объектов в комплексе сравнения (популяций, экотипов, клоновых групп и т. д. );

- k – количество анализируемых признаков, введенных в комплекс сравнения.

 

Полученная в таком порядке матрица (таблица) преобразованных нормированных значений обладает следующими свойствами:

- каждый столбец (соответствует набору значений нормированных показателей какого-либо признака у разных объектов сравниваемого комплекса объектов – популяций, экотипов, сортов, клонов и т. п. ) имеет нулевое среднее значение, т. е. сумма всех значений нормированного показателя равна «нулю»;

- среднее квадратическое отклонение нормированных значений от их средней величины «0» равно «единице».

 

Метод предусматривает возможность оценки статистического расстояния в евклидовом пространстве между реальными объектами – реальными популяциями, экотипами, клоновыми группами и т. п. при попарном их сравнении каждого с каждым. В этом случае количество сравнений будет существенно больше, чем при сравнении реальных объектов только с эталонным объектом. Существенно важным моментом в этом случае является возникающая возможность оценки статистической близости или удаленности одного объекта от другого по комплексу (из всех анализируемых) признаков. Тогда возникает и возможность оценки генетической близости сравниваемых объектов (при селекционной оценке): т. е. удается установить, какие из объектов наиболее сходны между собой по всему комплексу признаков, а какие – наиболее удалены друг от друга. Принципиально используется схема сравнения, как и при сравнении с эталонным объектом, только в этом случае каждый раз в качестве объекта сравнения поочередно выступает один из реальных объектов, и с ним сравниваются все остальные объекты. В этом случае расчет обобщенного статистического расстояния между реальными объектами при их попарном сравнении будет иметь вид (2):

, где:                (2):

- d_iy – обобщенное статистическое расстояние между двумя сравниваемыми объектами.;

- i = 1, 2, 3, …n – индекс порядкового номера одного из двух сравниваемых объектов;

- y = 1, 2, 3, …n – индекс порядкового номера другого из двух сравниваемых объектов;

- k – количество анализируемых признаков, введенных в комплекс сравнения.

 

Получаемые в итоге такого анализа результаты, представляют собой статистическую оценку обобщенного статистического расстояния между каждой из проанализированных пар объектов. Они неодинаковы, что соответствует различной степени статистической удаленности или близости между конкретными объектами, но при этом, и это очень важно, все полученные оценки сравнимы между собой, поскольку получены для единого многомерного статистического пространства, для одной и той же многомерной системы координат. На основании этого представляется возможным дать обобщенную оценку (единую для всех сравниваемых пар объектов) статистической близости или удаленности сравниваемых объектов: представляется возможным оценить какой из объектов наиболее близок к каждому из других или удален от него. Обобщенное статистическое расстояние измеряется единым критерием, единой единицей измерения общей для всех случаев сравнения объектов. Принципиально это соответствует любому измерению вообще, поскольку измерение есть сравнение с эталоном.

При использовании многочисленных признаков (целого комплекса различных признаков) для комплексного сравнительного анализа необходимо выдвижение рабочего условия о равной информативной значимости каждого из анализируемых признаков. В противном случае, когда признаки не равнозначны в информативном плане (существуют более значимые и менее значимые признаки) вводят так называемые коэффициенты ценности признака или весовые коэффициенты.

Базой обобщенного сравнения может выступать «эталонный объект» (эталонная популяция или эталонный экотип, эталонный сорт, эталонное насаждение эталонное плюсовое дерево и т. д. ), имеющий наилучшие (наибольшие в смысле размеров плодов, семян, ствола и т. п. или наименьшие в смысле количества колючек на побегах, отпада за единицу времени, поражаемости вредителями и болезнями и т. п. ) показатели. При этом наилучшие показатели могут быть введены только как комплекс наилучших показателей анализируемого комплекса популяций, экотипов, плюсовых деревьев, сортов и т. п. Здесь следует учитывать то, что «наилучшее значение» признака устанавливается по его реальному ненормированному значению (при сравнении показателей в исходной матрице), но в расчете статистического обобщенного расстояния используются соответствующие ему («лучшему значению») нормированные значения того же признака. В методологическом плане эталонный объект является абстракцией идеализации. В этом случае статистические координаты (С) эталонного объекта можно представить в виде (3):

С = (С₁, С₂, С₃, …, С_k)                                                                            (3)

 

Тогда расчет обобщенного статистического расстояния между эталонным объектом и каждым конкретным (i-м) реальным объектом (между эталонной популяцией и любой из реальных популяций) может быть представлен в виде (4):

d_i = 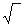(b_i1-c₁)²+(b_i2-c₂)²+(b_i3-c₃)²+…+(b_ik-c_k)², где:                           (4)

- d_i  – обобщенное статистическое расстояние между i-м реальным объектом и эталонным объектом.

 

Вместе с тем не исключена возможность введения параметров эталонного объекта как комплекса гипотетических параметров, которые должен иметь эталонный объект в соответствии с установленными задачами селекции или другой отрасли лесного хозяйства или лесной науки, даже если они не зафиксированы ни у одного объекта анализируемого комплекса. В этом случае параметры эталонного объекта вводятся в исходную матрицу и учитываются при расчете обобщенного среднего и обобщенного среднеквадратического отклонения. После этого преобразование матрицы исходных значений в матрицу нормированных значений производится по принятой ранее схеме.

Ограничением в этом случае может выступать то обстоятельство, что при расчетах обобщенного среднего и обобщенного среднеквадратического отклонения (используемых при нормировании материалов исходной матрицы) трудно учесть статистическое влияние гипотетических параметров гипотетического объекта на обобщенное среднее и обобщенное среднеквадратическое отклонение. Одним из путей преодоления этого ограничения может явиться такая схема расчета, при которой обобщенные статистики рассчитываются на основе статистической обработки материалов исходной матрицы средних, с условием введения в неё параметров гипотетического объекта: в исходную матрицу и соответственно ей – матрицу нормированных значений вводят дополнительную строку, содержащую оценки всех признаков эталонного объекта в количестве, соответствующем их количеству в исходной матрице.

Введение в комплекс сравнения эталонного объекта и оценка статистического расстояния между ним и каждым из реальных объектов позволяет дать оценку каждому из реальных объектов в смысле степени его приближения к эталонному объекту. Возникает возможность ранжировать анализируемые реальные объекты по критерию статистического расстояния между ними и эталонным объектом: чем ближе реальный объект к эталонному объекту, тем выше его оценка в принятой системе оценочных координат (признаков). При этом каждому из реальных объектов присваивается соответствующий ранг (от 1 до n) в зависимости от близости к эталонному объекту (табл. 3).

 

 

Таблица 3

Статистическое расстояние между природными (реальными)

и эталонной (гипотетической) популяциями облепихи

№ п/п	Популяции в поймах рек и в прибрежных зонах озер	Обобщенное статистическое расстояние
		по статистическому расстоянию в евклидовом пространстве		по обобщенному расстоянию Махаланобиса
		величина расстояния	ранговая оценка	величина расстояния	Ранговая оценка
1.	Бес-Агач	9, 061		80, 765
2.	Каркара	6, 829		38, 917
3.	Каинды	7, 995		59, 582
4.	Чилик	7, 194		49, 676
5.	Кульсай	7, 660		56, 920
6.	Большая Алма-Атинка	6, 420		36, 246
7.	Чу	9, 149		81, 268
8.	Усек	5, 841		33, 707
9.	Каратал	6, 291		38, 768
10.	Лепсы	6, 239		37, 573
11.	Аксай	6, 282		37, 646
12.	Бель-Булак	7, 346		49, 713
13.	Баян-Кол	7, 118		45, 391
14.	Тасты-Булак	7, 271		48, 967
15.	Зайсан	1, 587		2, 767

 

Используя критерий «норма», можно разделить весь комплекс сравниваемых объектов на три категории: «лучшие», «нормальные», «худшие». Критерий «норма» устанавливается в соответствии с величиной среднеквадратического отклонения обобщенного статистического расстояния. К «нормальным» относят объекты, имеющие величины обобщенного статистического расстояния, отклоняющиеся от средней величины обобщенного статистического расстояния на величину, равную 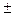2/3 σ. В эту категорию будут отнесены все объекты, которые имеют величину обобщенного статистического расстояния от эталонного объекта в пределах 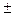2/3 σ от средней величины такого расстояния. К категории «лучших» будут относиться объекты, чьё статистическое расстояние до эталонного объекта меньше, чем минимальное значение границ «нормальности», т. е. меньше, чем средняя величина обобщенного статистического расстояния минус 2/3 σ. К категории «худших» будут относиться объекты, чьё обобщенное статистическое расстояние до эталонного объекта будет больше, чем величина максимальной границы «нормальности», т. е. больше, чем среднее значение обобщенного статистического расстояния плюс 2/3 σ. Для вычисления критерия «норма» полученные значения обобщенных статистических расстояний между реальными объектами и эталонным объектом рассматривают как вариационный ряд и рассчитывают для него среднюю величину и среднее квадратическое отклонение. Затем по формуле: М 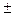2/3 σ вычисляют границы «нормальности»: верхнюю – по формуле М+2/3 σ; нижнюю – по формуле М–2/3 σ.

При выполнении настоящей лабораторной работы вычисление значений обобщенного статистического расстояния в многомерном пространстве признаков осуществляют для примера (Приложение 7. 1 и 7. 2) с плюсовыми деревьями сосны обыкновенной. Перечень и нумерация используемых в расчетах признаков плюсовых деревьев сосны обыкновенной представлены ниже. Вычисления ведут в электронных таблицах Excel.

При выборе признаков для комплексного анализа исходим из того, что объекты, их носители, должны иметь некоторую принципиальную общность характеристик (размещение на одном участке, одинаковый возраст, одинаковую степень развития учитываемых метамеров и т. п. ). В комплекс анализируемых признаков включались те, которые имеют хозяйственное, адаптивное и идентификационное значение. Для удобства введения в таблицы признакам были присвоены индексы (сокращенные названия). В частности для анализа ЛСП № 2 были задействованы как прямые признаки (непосредственно фиксируемые на объекте): высота дерева (пр. 1), диаметр ствола на высоте 1. 3 м (пр. 2), протяженность кроны по стволу (пр. 3), расстояние от корневой шейки до первого живого сучка (пр. 4), диаметр кроны вдоль ряда (пр. 5), диаметр кроны поперек ряда (пр. 6), длина хвои (пр. 7); так и производные признаки (получаемые посредством математических преобразований прямых признаков) абсолютный сбег ствола как отношение длины ствола к его диаметру на высоте 1. 3 м (пр. 8), объем ствола, вычисляемый по общепринятым формулам (пр. 9), относительное расстояние до первого живого сучка как отношение протяженности ствола до первого живого сучка к высоте дерева (пр. 10), относительная протяженность кроны как отношение протяженности кроны к высоте дерева (пр. 11), средний диаметр кроны как среднее арифметическое двух диаметров вдоль и поперек ряда (пр. 12), площадь проекции кроны как площадь круга с диаметром, равным среднему диаметру кроны (пр. 13), коэффициент пространственного объема кроны как объем цилиндра с высотой, равной высоте дерева, и с основанием, равным площади круга, диаметр которого равен среднему диаметру кроны (пр. 14), коэффициент пространственного объема дерева как объем цилиндра с высотой, равной высоте дерева, и с основанием, равным площади круга, диаметр которого равен среднему диаметру кроны (пр. 15), коэффициент формы кроны как отношение протяженности кроны к её среднему диаметру (пр. 16). Общее количество признаков многомерного пространства составило 16.

На основе обобщенных расстояний в многомерном евклидовом пространстве (пространстве признаков) осуществляют кластерный анализ и построение дендрограмм, примеры которых приведены ниже (рис. 7. 1)

 

 

         

 

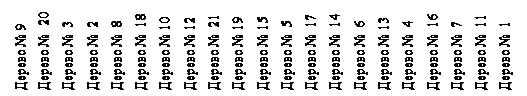
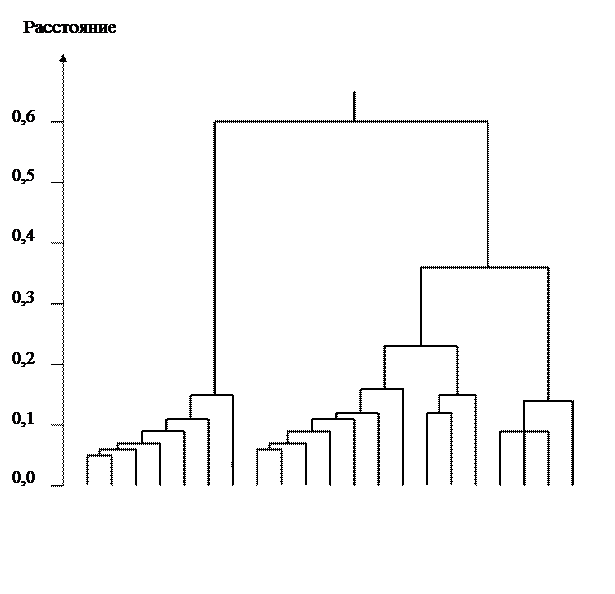
Рисунок 7. 1 – Дендрограмма соотносительной близости 21 плюсового дерева

в архиве клонов № 1, построенная в евклидовом пространстве 18 признаков

(представлены плюсовые деревья сосны обыкновенной)

 

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: