 |
6.5. Оценка компонентов вариансы
|
|
|
|
Собственно анализ комбинационной способности проводят по формулам, приведенным в таблице 3 и ниже.
Таблица 6. 3.
Схема дисперсионного анализа для определения комбинационной способности при одностороннем диаллельном скрещивании
плюсовых деревьев ели европейской
| № | Источники варьирования | Степени свободы | Сумма квадратов, S | Средний квадрат, М | Теоретически ожидаемое для среднего квадрата по модели 1 |
| 1. | ОКС Разница между семьями полусибсов | 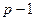
| Sg | Mg | 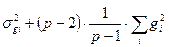
|
| 2. | СКС Разница между семьями сибсов | 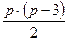
| Ss | Ms | 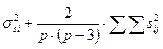
|
| 3. | Остаток (ошибка) | 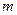 =
a× b× (c–1) =
a× b× (c–1)
| Se | Me | 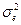
|
Вычисление компонентов дисперсионного анализа проводят в представленном ниже порядке.
Сумма квадратов, обусловленная общей комбинационной способностью (ОКС) вычисляется по формуле (4):
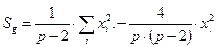 (4)
(4)
Сума квадратов, обусловленная специфической комбинационной способностью (СКС) вычисляется по формуле (5):
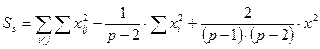 (5)
(5)
Достоверность эффектов общей и специфической комбинационной способности определяют с помощью F-критерия Фишера. Для эффектов общей комбинационной способности используем формулу (6):
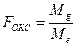 (6)
(6)
В соответствии с таблицей 6. 3, число степеней свободы равно:
- для значения Mg kg= p – 1;
- для значения Me’ ke= m.
Для эффектов специфической комбинационной способности используем формулу (7):
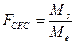 (7)
(7)
В соответствии с таблицей 3, число степеней свободы, в частности для Ms равно (8):
|
|
|
ks= p(p – 3)/2 (8)
Общую комбинационную способность любой родительской формы (i) определяют по формуле (9):
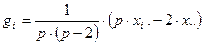 (9)
(9)
Варианса ОКС определенной родительской формы равна (10):
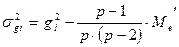 (10)
(10)
Специфическая комбинационная способность пары родительских компонентов (ij) определяют по формуле (11):
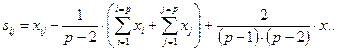 (11)
(11)
Варианса специфической комбинационной способности определенной родительской формы составляет (12):
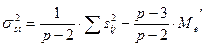 (12)
(12)
Порядок выполнения расчетов. Данное задание предусматривает последовательное решение комплекса задач, выполнение которых мы рассмотрим на уже использованном выше примере.
В рассматриваемом нами примере проводилось одностороннее прямое диаллельное скрещивание 6 родительских форм, в результате которого было получено 15 полусибсовых семей гибридного потомства F1. Количество гибридных семей (15) соответствует расчетному числу Гриффинга (1/2× р× (р – 1)). Варианты самоопыления исключались из схемы опыта. Характеристики родителей (плюсовых деревьев) также не учитывались. Испытание проводилось в шести повторностях (на 6 разных учетных участках испытательных культур или питомника) по 12 гибридных растений в каждой повторности. Анализировалась высота сеянцев в возрасте 20 лет. Средние значения анализируемого признака, представляющие собой средние арифметические значения по каждой полусибсовой семье из 6 повторностей с 12 гибридными сеянцами в каждой сведены в таблице 6. 4.
Таблица 6. 4.
Средняя для полусибсовой семьи высота ствола (см) у гибридов F1 ели Шренка и исходные значения для определения комбинационной способности её плюсовых деревьев (по Гужову, Фуксу, Валичеку, 1991)
|
|
|
| ♀ | ♂ | |||||||
| Р-1 | Р-2 | Р-3 | Р-4 | Р-5 | Р-6 | xi=Σ xij | xi2 | |
| Р-1 | 81, 1 | 83, 1 | 82, 2 | 81, 1 | 82, 0 | 409, 5 | 167690, 25 | |
| Р-2 | 81, 1 | 85, 1 | 85, 0 | 82, 0 | 85, 0 | 418, 2 | 174891, 24 | |
| Р-3 | 83, 1 | 85, 1 | 85, 9 | 85, 2 | 88, 0 | 427, 3 | 182585, 29 | |
| Р-4 | 82, 2 | 85, 0 | 85, 9 | 87, 4 | 88, 2 | 428, 7 | 183783, 69 | |
| Р-5 | 81, 1 | 82, 0 | 85, 2 | 87, 4 | 93, 0 | 428, 7 | 183783, 69 | |
| Р-6 | 82, 0 | 85, 0 | 88, 0 | 88, 2 | 93, 0 | 436, 2 | 190270, 44 | |
| Σ | 2548, 6 | 1083004, 60 | ||||||
Помимо экспериментально полученных данных, для каждой из 6 родительских форм ( xij. ), приведенных в верхней правой части матрицы, для каждого из 6 плюсовых деревьев вычисляют сумму значений признака (в данном примере по средним значениям для каждой комбинации скрещиваний) у F1 (F1 ij = Рi × Рj) соответствующей полусибсовой семьи: всех потомков-полусибсов отдельно для каждого из испытываемых плюсовых деревьев (Рi) в его сочетаниях со всеми другими (Рj). Величина имеет обозначение: ( xi = Σ xij ):
| х1 = 81, 1+83, 1+82, 2+81, 1+82, 0 = 409, 5 |
| х2 = 81, 1+85, 1+85, 0+82, 0+85, 0 = 418, 2 |
| х3 = 83, 1+85, 1+85, 9+85, 2+88, 0 = 427, 3 |
| х4 = 82, 2+85, 0+85, 9+87, 4+88, 2 = 428, 7 |
| х5 = 81, 1+82, 0+85, 2+87, 4+93, 0 = 428, 7 |
| х6 = 82, 0+85, 0+88, 0+88, 2+93, 0 = 436, 2 |
и соответствующие квадраты этих сумм ( xi2 = [Σ xij]2 ):
| х12 = (81, 1+83, 1+82, 2+81, 1+82, 0)2 = 409, 52 = 167690, 25 |
| х22 = (81, 1+85, 1+85, 0+82, 0+85, 0)2 = 418, 22 = 174891, 24 |
| х32 = (83, 1+85, 1+85, 9+85, 2+88, 0)2 = 427, 32 = 182585, 29 |
| х42 = (82, 2+85, 0+85, 9+87, 4+88, 2)2 = 428, 72 = 183783, 69 |
| х52 = (81, 1+82, 0+85, 2+87, 4+93, 0)2 = 428, 72 = 183783, 69 |
| х62 = (82, 0+85, 0+88, 0+88, 2+93, 0)2 = 436, 22 = 190270, 44 |
а также общую сумму этих квадратов сумм значений полусибсовых семей по каждому полному набору комбинаций скрещиваний каждого ПД ( Σ xi2 ); Σ xi2 = 1083004, 60.
Σ (Σ xij)2
На следующем этапе рассчитывают:
- сумму всех значений признака полученных в данной схеме испытаний полусибсовых семей (в рассматриваемом примере только прямые односторонние скрещивания): вычисляется как сумма полученных в данном испытании средних ( xij. ) по комбинациям (в нашем случае только прямые односторонние скрещивания, см. табл. 4) значений признака ( x.. = [Σ Σ xij. ] ):
| x.. = 81, 1+83, 1+82, 2+81, 1+82, 0 + |
| + 85, 1+85, 0+82, 0+85, 0 + |
| + 85, 9+85, 2+88, 0 + |
| + 87, 4+88, 2 + |
| + 93, 0 = |
| = 1274, 3 |
|
|
|
- квадрат этой суммы ( x.. 2 = [Σ Σ xij. ]2 ), x.. 2 = (1274, 3)2 = 1623840, 49;
- общую сумму квадратов значений признака всех гибридов F1 (F1 ij = Рi × Рj) – в нашем случае одностороннего скрещивания (только прямые скрещивания), ( Σ Σ x2ij. ), Σ Σ x2ij. = 108405, 73.
| Σ Σ x2ij. = 81, 12+83, 12+82, 22+81, 12+82, 02 + … |
| + 85, 12+85, 02+82, 02+85, 02 + … |
| + 95, 92+85, 22+88, 02 + … |
| + 87, 42+88, 22 + … |
| + 93, 02 = |
| = 108405, 73 |
Кроме того, вычисляют полную сумму сумм значений признака (в данном примере по приведенным средним значениям для каждой комбинации скрещиваний) у F1 (F1 ij = Рi × Рj) соответствующей полной полусибсовой семьи: всех потомков-полусибсов каждого одного из испытываемых плюсовых деревьев (Рi) в его сочетаниях со всеми другими (Рj) – ( Σ xi = Σ Σ xij, если xi = Σ xij ); показатель используется в расчетах оценок ОКС:
| Σ Σ xij = 81, 1+83, 1+82, 2+81, 1+82, 0 + Σ xi = 409, 5 + |
| + 81, 1+85, 1+85, 0+82, 0+85, 0 + 418, 2 + |
| + 83, 1+85, 1+85, 9+85, 2+88, 0 + + 427, 3 + |
| + 82, 2+85, 0+85, 9+87, 4+88, 2 + или + 428, 7 + |
| + 81, 1+82, 0+85, 2+87, 4+93, 0 + + 428, 7 + |
| + 82, 0+85, 0+88, 0+88, 2+93, 0 + 436, 2 = |
| = 2548, 6 = 2548, 6 |
полученная величина в формулах дальнейших расчетов ОКС обозначена как «2 × х.. ». Она соответствует общей сумме всех значений признака полусибсовых групп. Тогда для полной реципрокной схемы диаллельных скрещиваний получим ( Σ xi = Σ Σ xij ) Σ xi = 2548, 6.
Вычисление компонентов дисперсии проводят по следующим формулам, используя полученные на предыдущем этапе значения.
1. Сумма квадратов, обусловленная общей комбинационной способностью (ОКС) - Sg (13):
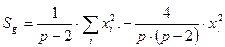 = 1/(6 – 2) × 1083004, 6 – 4/6 × (6 – 2) × 162384, 49 = 270751, 15 – 270640, 08 = 111, 07. (13)
= 1/(6 – 2) × 1083004, 6 – 4/6 × (6 – 2) × 162384, 49 = 270751, 15 – 270640, 08 = 111, 07. (13)
|
|
|
2. Сума квадратов, обусловленная специфической комбинационной способностью (СКС) - Ss (14):
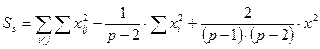 = 108405, 73 – 1/(6 – 2) × 1083004, 6 + + 2/[(6 – 1) × (6 – 2)] × 1623840, 49 = 108405, 73 – 270751, 15 + 162384, 05 = 38, 63. (14)
= 108405, 73 – 1/(6 – 2) × 1083004, 6 + + 2/[(6 – 1) × (6 – 2)] × 1623840, 49 = 108405, 73 – 270751, 15 + 162384, 05 = 38, 63. (14)
На следующем этапе составляют таблицу варианс (дисперсий).
Таблица 6. 5.
Таблица варианс для определения комбинационной способности
| Источники варьирования | Степень свободы | Сумма квадратов, S | Средний квадрат М |
| ОКС | 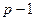 = 6 – 1 = 5 = 6 – 1 = 5
| Sg = 111, 07 | Мg = Sg /kg = 22, 21 |
| СКС | 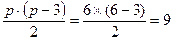
| Ss = 38, 63 | Мs = Ss /ks = 4, 29 |
| Остаток | 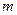 = 990 = 990
| Sе = | Ме = Sе/kе = 0, 08 |
Достоверность эффектов общей и специфической комбинационной способности определяют с помощью F-критерия Фишера.
Для эффектов общей комбинационной способности (15):
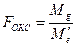 = 22, 21 / 0, 08 = 277, 6 (табличное значение 4, 37). (15)
= 22, 21 / 0, 08 = 277, 6 (табличное значение 4, 37). (15)
В соответствии с таблицей 6. 3, число степеней свободы равно:
- для значения Mg (16)
kg = p – 1 = 6 – 1 = 5; (16)
- для значения Me’ (17)
ke = m = a× b× (c–1) = 990. (17)
Для эффектов специфической комбинационной способности (18):
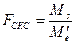 = 4, 29 / 0, 08 = 53, 6 (табличное значение 2, 71). (18)
= 4, 29 / 0, 08 = 53, 6 (табличное значение 2, 71). (18)
В соответствии с таблицей 6. 3, число степеней свободы равно:
- для значения Ms (19):
ks = p(p – 3)/2 = 9; (19)
- для значения Me’ (20):
ke = m = a× b× (c–1)= 990. (20)
Из представленных расчетов и сравнений видно, что и фактическое (опытное, эмпирическое) значение дисперсионного отношения (критерия Фишера) общей комбинационной способности и фактическое (опытное, эмпирическое) значение дисперсионного отношения (критерия Фишера) специфической комбинационной способности превышают соответствующие табличные значения. Это свидетельствует о том, что значения общей и специфической комбинационной способности достоверны. Полученный результат обусловливает возможность и целесообразность (создает основания, предпосылки для) продолжения генетического анализа, который будет состоять в определении общей комбинационной способности для каждой родительской формы (плюсового дерева) и специфической комбинационной способности для каждой их пары в прямых односторонних скрещиваниях.
При диаллельном скрещивании для каждого родительского компонента (i) – любой родительской формы – общую комбинационную способность (gi) определяют по формуле (21):
|
|
|
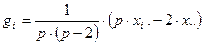 (21)
(21)
Варианса ОКС определенной родительской формы равна (22):
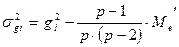 (22)
(22)
Тогда для каждой из родительских форм (плюсового дерева) получим следующие значения общей комбинационной способности (gi):
g1 = 1/[6× (6 – 2)] × (6 × 409, 5 – 2 × 1274, 3) = – 3, 82;
g2 = 1/[6× (6 – 2)] × (6 × 418, 2 – 2 × 1274, 3) = – 1, 64;
g3 = 1/[6× (6 – 2)] × (6 × 427, 3 – 2 × 1274, 3) = 0, 63;
g4 = 1/[6× (6 – 2)] × (6 × 428, 7 – 2 × 1274, 3) = 0, 98;
g5 = 1/[6× (6 – 2)] × (6 × 428, 7 – 2 × 1274, 3) = 0, 98;
g6 = 1/[6× (6 – 2)] × (6 × 439, 2 – 2 × 1274, 3) = 2, 86.
Оценки вариансы для ОКС каждой особи получают в результате следующих расчетов:
σ gi = – 3, 822 – (6 – 1)/[6× (6 – 2)] × 0, 08 = 14, 58;
σ gi = – 1, 642 – (6 – 1)/[6× (6 – 2)] × 0, 08 = 2, 67;
σ gi = 0, 632 – (6 – 1)/[6× (6 – 2)] × 0, 08 = 0, 38;
σ gi = 0, 982 – (6 – 1)/[6× (6 – 2)] × 0, 08 = 0, 94;
σ gi = 0, 982 – (6 – 1)/[6× (6 – 2)] × 0, 08 = 0, 94;
σ gi = 2, 862 – (6 – 1)/[6× (6 – 2)] × 0, 08 = 8, 16.
Расчеты для каждой родительской формы сводят в таблицу 6. 6.
Таблица 6. 6.
Общая комбинационная способность родительских форм (плюсовых деревьев ели Шренка)
| Родительский компонент | gi | σ gi |
| Р1 | - 3, 82 | 14, 58 |
| Р2 | - 1, 64 | 2, 67 |
| Р3 | 0, 63 | 0, 38 |
| Р4 | 0, 98 | 0, 94 |
| Р5 | 0, 98 | 0, 94 |
| Р6 | 2, 86 | 8, 16 |
Специфическая комбинационная способность пары родительских компонентов (ij) определяют по формуле (23):
 , где: (23)
, где: (23)
- xi-j – среднее значение признака всех потомков-сибсов каждой конкретной комбинации скрещивания двух родителей (Pi × Pj), участвующих в испытаниях потомств;
- xi – сумма значений признака F1 соответствующей полусибсовой группы (всех потомков-полусибсов одного из родителей, во всех его комбинациях с каждым их других плюсовых деревьев) – «первого» из двух родителей (Pi) со всеми остальными;
- xj – сумма значений признака F1 соответствующей полусибсовой группы (всех потомков-полусибсов одного из родителей, во всех его комбинациях с каждым их других плюсовых деревьев) – «второго» из двух родителей (Pj) со всеми остальными;
- x.. – общая сумма значений признака всех полусибсовых групп (всех полученных в опыте потомков-полусибсов) реализованной в данной опыте (схеме) испытаний потомств прямой схемы диаллельных скрещиваний.
Варианса специфической комбинационной способности определенной родительской формы составляет (24):
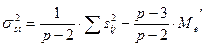 (24)
(24)
Для всех комбинаций прямого одностороннего скрещивания плюсовых деревьев, участвующих в испытаниях потомств, принадлежащих родителям «первому» и «второму» (Р1 × Р2) получим:
S1-2 =x1-2 –1/(6–2)× (x1+x2)+2/(6–1)× (6–2)× x.. =81, 1–¼ × (409, 5+418, 2)+2/20× (1274, 3)=1, 60
S1-3 =x1-3 –1/(6–2)× (x1+x3)+2/(6–1)× (6–2)× x.. =83, 1–¼ × (409, 5+427, 3)+2/20× (1274, 3)=1, 33
S1-4 =x1-4 –1/(6–2)× (x1+x4)+2/(6–1)× (6–2)× x.. =82, 2–¼ × (409, 5+428, 7)+2/20× (1274, 3)=0, 08
S1-5 =x1-5 –1/(6–2)× (x1+x5)+2/(6–1)× (6–2)× x.. =81, 1–¼ × (409, 5+428, 7)+2/20× (1274, 3)=-1, 02
S1-6 =x1-6 –1/(6–2)× (x1+x6)+2/(6–1)× (6–2)× x.. =82, 0–¼ × (409, 5+436, 2)+2/20× (1274, 3)=-2, 00
S2-3 =x2-3 –1/(6–2)× (x2+x3)+2/(6–1)× (6–2)× x.. =85, 1–¼ × (418, 2+427, 3)+2/20× (1274, 3)=1, 16
S2-4 =x2-4 –1/(6–2)× (x2+x4)+2/(6–1)× (6–2)× x.. =85, 0–¼ × (418, 2+428, 7)+2/20× (1274, 3)=0, 70
S2-5 =x2-5 –1/(6–2)× (x2+x5)+2/(6–1)× (6–2)× x.. =82, 0–¼ × (418, 2+428, 7)+2/20× (1274, 3)=-2, 30
S2-6 =x2-6 –1/(6–2)× (x2+x6)+2/(6–1)× (6–2)× x.. =85, 0–¼ × (418, 2+436, 2)+2/20× (1274, 3)=-1, 17
S3-4 =x3-4 –1/(6–2)× (x3+x4)+2/(6–1)× (6–2)× x.. =85, 9–¼ × (427, 3+428, 7)+2/20× (1274, 3)=-0, 67
S3-5 =x3-5 –1/(6–2)× (x3+x5)+2/(6–1)× (6–2)× x.. =85, 2–¼ × (427, 3+428, 7)+2/20× (1274, 3)=-1, 37
S3-6 =x3-6 –1/(6–2)× (x3+x6)+2/(6–1)× (6–2)× x.. =88, 0–¼ × (427, 3+436, 2)+2/20× (1274, 3)=-0, 44
S4-5 =x4-5 –1/(6–2)× (x4+x5)+2/(6–1)× (6–2)× x.. =87, 4–¼ × (428, 7+428, 7)+2/20× (1274, 3)=0, 48
S4-6 =x4-6 –1/(6–2)× (x4+x6)+2/(6–1)× (6–2)× x.. =88, 2–¼ × (428, 7+436, 2)+2/20× (1274, 3)=-0, 60
S5-6 =x5-6 –1/(6–2)× (x5+x6)+2/(6–1)× (6–2)× x.. =93, 0–¼ × (428, 7+436, 2)+2/20× (1274, 3)=4, 20
|
|
|


