 |
Вопрос 1. Виды проецирования. Образование ортогонального чертежа на одной и трех плоскостях проекций. Метод Монжа. (зад.6,8,9,11,12)
|
|
|
|
Вопрос 1. Виды проецирования. Образование ортогонального чертежа на одной и трех плоскостях проекций. Метод Монжа. (зад. 6, 8, 9, 11, 12)
Методы проецирования:
1). Центральное проецирование.
Проецирующие лучи выходят из центра проецирования.
П1- плоскость проекции.
S - центр проецирования.
Треуг. ABC – объект проецирования.
SA, SB, SC – проецирующие лучи.
Треуг. A1B1C1 – проекция треуг. ABC на пл-ть П1.
2). Параллельное проецирование.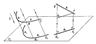 
(частный случай центрального проецирования с бесконечно удалённым центром проекций). Осуществляется оно пучком параллельных проецирующих лучей заданного направления.
(проецирующие лучи ведутся до пересечения их с П1).
Обр. орт. черт на одной проекции.
Построим орт. проекцию предмета на П1. На этом чертеже можно измерить длину и ширину, а высоту можно указать числом. (название проекции с числовыми отметками).
Обр. орт. черт на 3х проекциях.
П1 – горизонтальная пл-ть проекции
П2 – фронтальная пл-ть проекции
П3 – профильная пл-ть проекции
Плоскости проекций, пересекаясь меж собой, образуют оси координат:
П1 П2=х Расстояние от точки до пл-тей проекции наз. координатами точек.
П1 п3=у
П2 П3=z
ХА – расстояние от т. до проф. пл-ти проекции.
ХА=АА3=АхО=А1Ау=А2Аz
УА – расстояние от т. до фронт. пл-ти проекции
АУ=АА2=А1Ах=А3А2
ZА – расстояние от т. до горизонтальной пл-ти проекции
ZA=АА1=АzО=АzAx=A3Ay
Прямая, соединяющая две проекционные точки, наз. линией связи. Она всегда оси.
Метод Монжа.
Метод параллельного проецирования (при чём берутся прямоугольные проекции на 2 взаимно плоскости проекции). Например на П1 и П2. Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П1 совмещают вращением вокруг оси x12 с плоскостью П2 (рис. 1. 6). Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называется эпюром (Франц. Epure – чертеж. ). Эпюр часто называют эпюром Монжа.
|
|
|
Вопрос 2. Линии. Классификация линий. Прямая линия. Классификация прямых по расположению относительно друг друга и по расположению относительно плоскостей проекций. Принадлежность точки прямой. (зад. 14, 13)
Любую линию можно рассматривать как результат перемещения некоторой точки в пространстве. При этом все множество линий можно разделить на прямые, кривые и пространственные.
Прямую можно задать на чертеже в виде отрезка.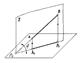 
Между длинами отрезка АВ и А1В1 имеется зависимость А1В1=АВcosфи, где
Фи - угол между отрезком и плоскостью проекций. При фи = 0о отрезок проецируется в натуральную величину, при фи=90о – в точку.
Кривые: циркульные и лекальные.
Циркульные: эллипс, парабола, гипербола, окружность.
Пространственные: винтовая линия.
Взаимное расположение прямых.
Прямые в пространстве могут пересекаться, быть взаимно параллельными (пересекаться в бесконечно удаленной точке) и скрещиваться.
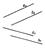Если прямые пересекаются, то их одноименные проекции также пересекаются, причем точки пересечения одноименных проекций таких прямых лежат на одной линии связи
Если прямые параллельны, то их одноименные проекции также параллельны.
Если прямые скрещиваются, то их одноименные проекции могут пересекаться или на одной проекции пересекаться, а на второй - быть параллельными.
Расположение прямых относ. Плоск. пр-ии.
Прямые: общего и частного положения.
Прямой общего положения называют прямую, не параллельную ни одной из данных плоскостей проекций. Любой отрезок такой прямой проецируется в данной системе плоскостей проекций искаженно. Искаженно проецируются и углы наклона этой прямой к плоскостям проекций.
|
|
|
К прямым частного положения относятся прямые, параллельные одной или двум плоскостям проекций. Различают три основные линии уровня: горизонталь, фронталь и профильную линии.
Горизонталью называют любую линию, параллельную горизонтальной плоскости проекций. Любой отрезок горизонтали проецируется на П1 без искажения. В ист. величину проецируется и угол наклона горизонтали к П2.
Фронталью называют линию, параллельную фронтальной плоскости проекций. Любой отр. фронтали проецируется без искажения на П2. Угол наклона фронтали к П1 проецируется на П2 без искажения.
Профильной линией называют линию, параллельную профильной плоскости проекций. Любой отрезок профильной линии (прямой) проецируется на профильную плоскость в истинную величину. На эту же плоскость проецируются в истинную величину и углы наклона профильной прямой к плоскостям проекций П 1 и П 2
Прямая паралл. 2м пл-тям проекции будет перп. 3ей и наз. проецирующей прямой.
Прямая перп. П1 – гориз. проец., П2-фронт. проец., П3-проф. проец.
Принадлежность прямой точке.
Точка принадлежит прямой, если соответствующие проекции точки расположены на соответствующих проекциях прямых.
|
|
|
