 |
Вопрос 13. Пересечение плоскости с гранным геометрическим телом и с цилиндром. Построение проекций и натуральной величины наклонного сечения проецирующей плоскостью.
|
|
|
|
Вопрос 13. Пересечение плоскости с гранным геометрическим телом и с цилиндром. Построение проекций и натуральной величины наклонного сечения проецирующей плоскостью.
Сечение гранного тела.
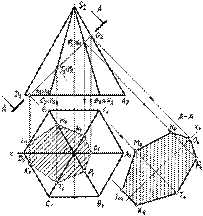Сечение цилиндра.
Если секущая плоскость будет проходить через образующие, то в сечении получим параллельные прямые, если через направляющие, то - окружность. Все остальные сечения цилиндра будут эллипсами. Построение сечения цилиндра фронтально проецирующей плоскостью рассмотрено на рис. 8. 2.
Натуральную величину сечения построим по точкам. Отметим на чертеже точки, соответствующие большой АВ и малой CD осям эллипса
Вопрос 14. Наклонные сечения конуса и шара. Построение проекций и натуральной величины наклонного сечения проецирующей плоскостью.
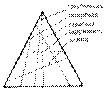Сечение конуса.
Если секущая плоскость будет проходить через образующую (прямую), то в сечении получим треугольник, если через направляющую (окружность) - окружность.
Все остальные сечения кругового конуса будут лекальными кривыми второго порядка, а именно: - эллипсом, когда секущая плоскость пересекает все образующие конуса; - параболой - секущая плоскость параллельна одной из образующих; - гиперболой - секущая плоскость параллельна двум образующим.
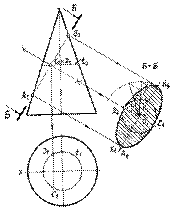На рис. 8. 4 выполнен чертеж конуса, и показана секущая плоскость Б - Б, которая пересекает все образующие данного конуса. Следовательно, фигура сечения будет ограничена эллипсом, а отрезок А 2 B 2 является его фронтальной проекцией
Натуральную величину сечения можно построить по законам построения эллипса. Для этого на оси х откладываем большую ось эллипса АВ и малую CD. Причем, малая ось эллипса определяется как хорда ( CD ) параллели, делящей пополам фронтальную проекцию сечения.
|
|
|
Сечение шара.
Как известно, любое сечение шара плоскостью является кругом. В зависимости от положения секущей плоскости, окружность, ограничивающая фигуру сечения, может спроецироваться в:
- окружность, если секущая плоскость параллельна плоскости проекций;
- отрезок прямой, если секущая плоскость перпендикулярна плоскости проекций;
- эллипс, если секущая плоскость наклонена к плоскости проекций.
Так как сечение шара - круг (рис. 8. 7), то построение его натуральной величины сводится к определению радиуса окружности. Участок линии сечения А 3 В 3 является диаметром этой окружности. Поэтому для построений на новую ось х 1 линиями связи переносятся точки О и В, после чего радиусом, равным расстоянию между ними, проводится окружность - граница фигуры сечения А - А.
Билет 15. Построение проекций и натуральной величины наклонного сечения плоскостью общего положения на примере многогранника и конуса.
См. билет 13 и 14.
Билет 16. Построение точки пересечения прямой с поверхностью вращения. Пересечение многогранника с поверхностью вращения на примере соосных конуса и шестигранной призмы. (зад. 56, 59)
Построение точки встречи прямой общего положения с проецирующей поверхностью
Найдем точки встречи прямой d с цилиндрической поверхностью, заданной направляющей 1 и образующей s (рис. 7. 9).
Как видно из чертежа, поверхность цилиндра является горизонтально проецирующей. Следовательно, горизонтальные проекции всех точек, принадлежащих поверхности, совпадут с 1 1 - проекцией цилиндрической поверхности на плоскость П 1. Поэтому на пересечении 1 1 и d 1 отмечаем А 1 и В 1, которые и будут горизонтальными проекциями точек встречи прямой и поверхности.
Фронтальные проекции А 2 и В 2 искомых точек построим при помощи линий связи на d 2 - фронтальной проекции прямой.
|
|
|
Построим точки встречи прямой 1 с поверхностью сферы. Заключим прямую 1 в горизонтально проецирующую плоскость Г ( Г 1 º 1 1). Эта плоскость пересечет сферу по окружности, которая на плоскость П 2 спроецируется в эллипс с большой С 2 D 2 и малой Е 2 F 2 осями. В пересечении фронтальной проекции 1 2 прямой 1 с эллипсом получим А 2 и В 2 -фронтальные проекции искомых точек.
Приведенное решение является недостаточно точным, так как сам эллипс надо строить по точкам. Более точно эту задачу можно решить методом проецирования на дополнительную плоскость (рис. 7. 12).
Построим третью проекцию на плоскость П 4, параллельную плоскости Г. В новой системе плоскостей проекций П 4 ^ П 1 построим О 4 и 1 4 - проекции центра шара и прямой 1 на плоскость П 4. На П 4 окружность сечения спроецируется неискаженно в виде окружности радиуса 1 4 2 4. Пересечение этой окружности с 1 4 дает проекции А 4 и В 4 искомых точек, имея которые, легко построить их горизонтальные А 1, В 1 и фронтальные А 2, В 2 проекции.
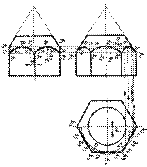
Пример построения точек встречи горизонтальной прямой 1 с поверхностью тора.
Искомые точки А ( А 1, А 2), B ( В 1, В 2), C ( С 1, С 2), D ( D 1, D 1) найдены при помощи вспомогательной горизонтальной плоскости W ( W 2), которая рассекает поверхность тора по параллелям радиусов О 1 и О 2. Количество точек пересечения прямой с поверхностью в общем случае определяет порядок поверхности. Действительно, тор - поверхность четвертого порядка, и прямая пересекает его поверхность в четырех точках A, B, C, D.
В приведенных примерах в качестве вспомогательных плоскостей использовались проецирующие плоскости. Рассмотрим ряд случаев, в которых более целесообразно в качестве вспомогательных плоскостей использовать плоскости общего положения.
Построим точки встречи прямой 1 с поверхностью конуса (рис. 7. 14). Конус задан своей вершиной S ( S 2, S 2) и направляющей k, лежащей в плоскости W.
В данном случае применять вспомогательные проецирующие плоскости не рационально, так как эти плоскости не дадут графически простых линий сечения. Если же провести вспомогательную плоскость через прямую 1 и вершину S конуса, то такая плоскость (общего положения) даст в сечении конуса графически простые линии - образующие.
Возьмем на прямой 1 произвольную точку О и, соединив ее с вершиной S конуса, определим плоскость Г ( 1 Ç t, проходящую через прямую 1 и вершину S конуса.
Плоскость Г пересечет плоскость W основания, в которой лежит направляющая k конуса, по прямой 12 ( 1 1 2 1, 1 2 2 2). Пересечение прямой 1 2 с направляющей k конуса даст точки D и Е, через которые проводим образующие SD и SE. Пересечение этих образующих с прямой 1 даст искомые точки: 1 Ç SD = A; 1 Ç SE = В.
В случае пересечения соосных конуса и шестигранной призмы
|
|
|
|
|
|
