 |
Вопрос 4. Пересечение прямой и плоскости (3 случая). (зад.30,32)
|
|
|
|
Вопрос 3. Плоскость, задание на чертеже. Классификация плоскостей по расположению относительно плоскостей проекций. Принадлежность точки и прямой плоскости. Главные линии плоскости.
Плоскость можно рассматривать как результат перемещения прямолинейной образующей l, все время оставаясь параллельной прямой b, вдоль направляющей а. При этом а является также прямой (рис. 3. 5). Определитель плоскости записывается следующим образом: F ( l, а )[ l ½ ½ b ].
Задание плоскости тремя точками.
Три точки, не лежащие на одной прямой, задают плоскость (рис. 3. 6а). Любая четвертая, пятая и т. д. точки, взятые произвольно на чертеже, как правило, не принадлежат заданной плоскости. Определитель: S ( A, B, C ).
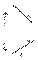Задание плоскости прямой и точкой вне этой прямой.
Если две точки плоскости соединить прямой, то получим задание плоскости прямой и точкой
Всякий дополнительный элемент (точка, прямая), взятый произвольно, как правило, не будет принадлежать этой плоскости. Определитель: S ( A, b )[ AË b ].
Задание плоскости двумя пересекающимися прямыми.
Две пересекающиеся прямые определяют плоскость. Определитель: S(а b)
В ряде случаев плоскость удобно задавать двумя пересекающимися прямыми уровня: горизонталью и фронталью.
Задание плоскости двумя параллельными прямыми.
Так как параллельные прямые можно рассматривать как пересекающиеся в несобственной точке, то они также будут определять плоскость. Определитель: S ( a ½ ½ b )
Задание плоскости плоской фигурой (отсек плоскости).
Любая плоская фигура, например треугольник, задает плоскость. Плоская фигура придает большую наглядность изображаемой плоскости. Определитель: S ( ABC ).
|
|
|
Класс. пл-тей относ. пл-тей проекции.
Пл-ти: общего и частного положения
Пл-ть перп. Одной пл-ти проекции наз проецирующей.
Пл-ть перп. П1 – гориз проец, П2-фронт проец, П3 – проф проец.
Пл-ть перп. 2м плоскостям проекции будет паралл 3ей и наз. плоскостью уровня.
Пл-ть паралл. П1-гориз. Пл-ть уровня, П2- фронт. п. ур., П3 – проф. пл. ур.
Принадлежность точки, прямой плоскости.
Прямая принадлежит пл-ти, если она проходит через 2 точки, принадл. пл-ти.
Точка принадлежит пл-ти, если она расположена на прямой, принадл. пл-ти.
Главные линии плоскости.
.. наз. прямые уровня принадл. пл-ти, а также линии наибольшего наклона к плоскости проекции. (задача 20) Линии наиб. наклона к пл-тям проекции – прямые принадл. пл-ти и перп линиям уровня пл-ти.
Линией ската или л. наиб накл к П1 наз прямую принадл пл-ти и перп горизонтали пл-ти.
Линией наиб. наклона к П2 наз. прямую принадл пл-ти и перпфронтали пл-ти.
Вопрос 4. Пересечение прямой и плоскости (3 случая). (зад. 30, 32)
1). Пересечение проецирующей пр-ой с пл-тью общего положения.
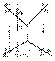На рис. 7. 5 показано построение точки встречи горизонтально проецирующей прямой n с плоскостью общего положения Q ( a Ç b ). Горизонтальные проекции всех точек, принадлежащих данной прямой, в том числе и горизонтальная проекция М 1 искомой точки М, будут совпадать с n 1 - горизонтальной проекцией прямой n. Следовательно, задача сводится к нахождению недостающей фронтальной проекции М 1 точки М, лежащей в плоскости Q. Через М 1 проведем прямую 1 1 2 1. По линиям связи найдем фронтальные проекции 1 2, 2 2 точек 1 и 2, через которые проведем фронтальную проекцию прямой 12. На пересечении 1 2 2 2 с n 2 и будет находиться фронтальная проекция М 2 точки М.
2). Пересечение проецирующей пл-ти с прямой общ. положения. построим точку встречи фронтально проецирующей плоскости Q с прямой общего положения n (рис. 7. 4). Пусть n Ç Q = = М. М 2 - фронтальная проекция искомой точки М должна лежать на фронтальной проекции П 2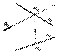 
прямой n, как точка, принадлежащая прямой n. В то же время фронтальная проекция М 2 точки М должна лежать на следе Q 2 плоскости Q , так как искомая точка принадлежит и плоскости Q. Следовательно, искомая фронтальная проекция М 2 точки М может лежать только на пересечении n 2 и Q 2. Имея фронтальную проекцию М 2 точки М, при помощи линии связи легко найти ее горизонтальную проекцию.
|
|
|
зад. 30
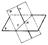3). Пересечение прямой общего положения с пл-тьюобщего положения.
1) через прямую проводят вспомогательную плоскость F ;
2) находят линию пересечения 1 данной Q и вспомогательной F плоскостей;
3) отмечают искомую точку М как точку пересечения прямой 1 с данной прямой n.
Зад. 32.
|
|
|
