 |
Вопрос 5. Пересечение плоскостей (2 случая).
|
|
|
|
Вопрос 5. Пересечение плоскостей (2 случая).
1). Пересечение 2х пл-тей общего положения.
Зад. 35.
Алгоритм.
1. Пересечем заданные плоскости Г и W вспомогательной плоскостью-посредником S.
2. Построим линии пересечения плоскостей Г и W с плоскостью S. Это будут соотвественно прямые с и 1.
3. Строим точку А пересечения прямых с и 1. Эта точка, с одной стороны, принадлежит прямой с. Следовательно, она принадлежит плоскости Г. С другой стороны, эта точка принадлежит прямой 1. Следовательно, она принадлежит плоскости S 1. Точка, принадлежащая одновременно двум плоскостям, принадлежит линии их пересечения.
4. Вводим вторую вспомогательную плоскость F , с помощью которой получаем вторую общую для двух плоскостей точку В.
5. Через две точки проводим прямую, которая и будет линией пересечения плоскостей Г и W.
2). Пересечение проецирующей пл-ти с пл-тью общего положения.
Линия пересечения представляет собой множество точек, принадлежащих одновременно двум поверхностям, в данном случае - плоскостям. Две плоскости будут пересекаться по прямой.
Одна из плоскостей S (рис. 7. 1) является фронтально проецирующей, т. е. перпендикулярной фронтальной плоскости проекций ( S ^ П 2). В этом случае фронтальная проекция любой линии, принадлежащей плоскости S, будет совпадать с фронтальной проекцией плоскости S. Следовательно, фронтальная проекция 1 2 2 2 линии пересечения 12 плоскостей S и Г на чертеже имеется. Горизонтальную проекцию 1 1 2 1 строим по принадлежности линии непроецирующей плоскости Г.
Вопрос 6. Пересечение многогранников. (зад. 57)
Алгоритм: Определят точки в которых рёбра одной поверхности пересекают грани другой и рёбра второй пересекают грани первой. Через найденные точки в определённой последовательности проводят ломаную линию, представляющую собой линию пересечения данных поверхностей. При этом можно соединять прямыми проекции лишь тех точек, полученных в процессе построения, которые лежат в одной и той же грани.
|
|
|
Вопрос 7. Образование и задание поверхностей на чертеже. Кинематический и каркасный способы. Определитель поверхности. Классификация поверхностей. Порядок поверхности.
В инженерной графике поверхность рассматривают как множество последовательных положений линии, перемещающейся в пространстве по определенному закону.
Перемещающаяся линия 1 называется образующей, неподвижные линии a, b, c - направляющими.
Кинематический способ.
Здесь в качестве образующей взята прямая 1. Закон перемещения образующей задан направляющей а и прямой b. При этом имеется в виду, что образующая 1 скользит по направляющей а, все время оставаясь параллельной прямой b.
Каркасный способ.
Задание поверхности множеством принадлежащих ей точек или линий. При этом точки и линии выбирают так, чтобы они давали возможность с достаточной степенью точности определять форму поверхности и решать на ней различные задачи.
Множество точек или линий, определяющих поверхность, называют ее каркасом.
Определитель поверхности - совокупность независимых условий, однозначно задающих поверхность.
Определитель поверхности состоит из двух частей: геометрической и алгоритмической.
В геометрическую часть определителя входят геометрические фигуры и отношения между ними. В алгоритмическую часть - закон образования поверхности.
Чтобы отличить геометрическую часть определителя от алгоритмической, первую заключают в круглые скобки, а вторую - в квадратные. Тогда определитель произвольной поверхности будет иметь следующую форму:
|
|
|
Ф ( Г )[ А ],
где ( Г ) - геометрическая часть; [ А ] - алгоритмическая часть.
Определитель поверхности прямого кругового конуса (рис. 3. 3), образованного вращением образующей 1 вокруг оси i.
Ф(l Ç a )[l вращается вокруг a]
классификация поверхностей.
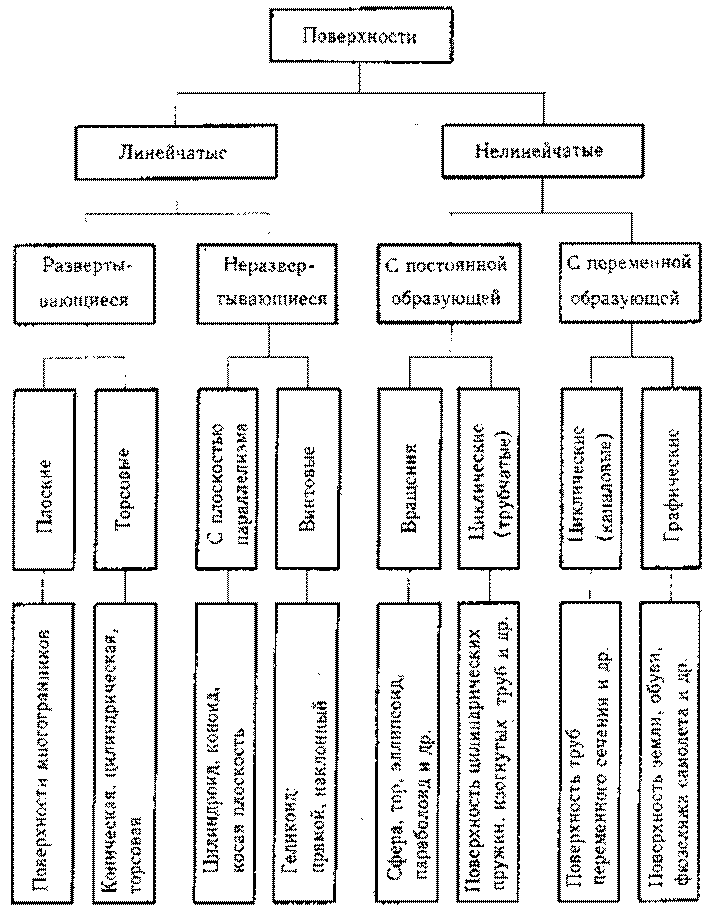
Порядок поверхности – максимальное число точек пересечения поверхности с прямой.
|
|
|
