 |
Задача 21. Осевое усилие на винте для подъёма детали поз.3 Рос= , где
|
|
|
|
Задача 21
 Определить момент Тзав, прикладываемый к винту поз. 1, для подъёма детали поз. 3, нагруженной силой Р, посредством перемещения клина поз. 2. Исходные данные: средний диаметр резьбы винта d2=15мм., приведенный угол трения в резьбе j = 9, 6480, угол подъёма резьбы y = 2, 4310, угол клина поз. 2 а = 100, коэффициент трения при перемещении клина по обеим поверхностям f=0, 1. Трением на торце винта и детали поз. 3 пренебречь. Значение силы Р приведено в таблице.
Определить момент Тзав, прикладываемый к винту поз. 1, для подъёма детали поз. 3, нагруженной силой Р, посредством перемещения клина поз. 2. Исходные данные: средний диаметр резьбы винта d2=15мм., приведенный угол трения в резьбе j = 9, 6480, угол подъёма резьбы y = 2, 4310, угол клина поз. 2 а = 100, коэффициент трения при перемещении клина по обеим поверхностям f=0, 1. Трением на торце винта и детали поз. 3 пренебречь. Значение силы Р приведено в таблице.
Задачу решить по одному из вариантов силы Р.
| P, кН |
Порядок решения:
Осевое усилие на винте для подъёма детали поз. 3 Рос=  , где
, где
Ptq(a+j) - вертикальная сила, создаваемая при перемещении клина поз. 2,
 =arqtqf - угол трения в клине, Рf - сила трения между клином поз. 2 и корпусом,
=arqtqf - угол трения в клине, Рf - сила трения между клином поз. 2 и корпусом,
Росf - сила трения между деталью поз. 3 и корпусом.
Момент, который необходимо приложить к винту поз. 1 для получения силы Рос
Тзав =  , где -
, где - 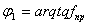 - угол трения в резьбе,
- угол трения в резьбе, 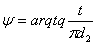 -угол
-угол
подъёма резьбы, t - шаг резьбы.
Окончательное решение  .
.
Задача 22

При исследовании механических характеристик материала, испытываемый образец 1 зажимается в клиновых плашках 2 клиновой головки 3 разрывной машины и подвергается растяжению силой Р.
Определить максимально возможный угол «a», при котором произойдёт самозаклинивание образца в плашках от силы растяжения, а также контактные напряжения между плашками и головкой.
Исходные данные:
- коэффициент трения между плашками и образцом f1 =0, 3.
- высота плашек h =100мм.
- длина плашек l =100мм.
Величина силы Р и коэффициента трения f2 между плашками и клиновой головкой приведены в таблице.
Задачу решить по одному из вариантов.
|
|
|
| Р, кН | ||||||||||
| f2 | 0, 16 | 0, 15 | 0, 14 | 0, 13 | 0, 12 | 0, 11 | 0, 1 | 0, 09 | 0, 08 | 0, 06 |
Порядок решения:
j2
р2
рт1
j1
р
рn
a
рт2
р2
 Сила растяжения Р передаётся на испытываемый пруток по контакту с плашками и на зажимную головку по контакту с плашками. Из рисунка видно Pn =
Сила растяжения Р передаётся на испытываемый пруток по контакту с плашками и на зажимную головку по контакту с плашками. Из рисунка видно Pn = 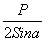 .
.
Контактное давление между плашкой и головкой  .
.
Условие самозаклинивания будет выполнено если сила трения между прутком и плашками будет больше чем сила трения между плашками и головкой, т. е. Рт1> Рт2. Рт1=Р2f1 или 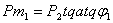 ;
;  - угол трения между прутком и плашкой. Сила трения Рт2 (см. рис. ) с учётом угла клина " a" Рт2 =Р2
- угол трения между прутком и плашкой. Сила трения Рт2 (см. рис. ) с учётом угла клина " a" Рт2 =Р2  , где
, где  - угол трения между плашкой и головкой (
- угол трения между плашкой и головкой ( 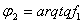 ).
).
 или
или  или
или 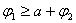 .
.
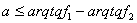 .
.
 Задача 23
Задача 23
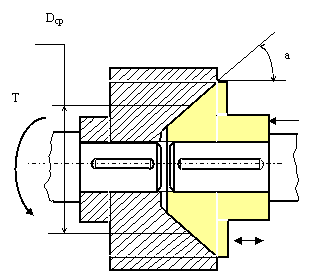
Определить силу Fa осевого прижатия простейшей конической муфты трения, необходимую для передачи крутящего момента Т = 100МПа при среднем диаметре муфты Dср = 200мм. и коэффициенте трения между полумуфтами f = 0, 1. Значение угла а приведено таблице. Задачу решить по одному из вариантов.
| а0 |
Порядок решения:
Dср
в
Р
а
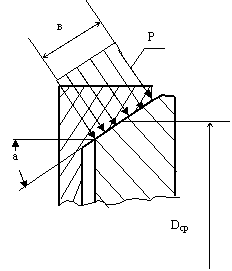
От действия силы Fa на конической поверхности соприкосновения полумуфт возникает удельное давление Р и удельные силы трения Рf. Силы трения, направленные по касательной к окружности конуса, используются для передачи крутящего момента. Рассматривая равновесие правой полумуфты получим: 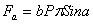
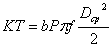 , решаем совместно
, решаем совместно 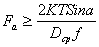 , здесь K - коэффициент запаса по трению.
, здесь K - коэффициент запаса по трению.
Минимально возможный угол конуса " a" должен быть больше угла трения материала полумуфт. Данная полумуфта не допускает смещения и перекоса соединяемых валов.
 Задача 24
Задача 24
На рисунке упрощенно показана кулачковая муфта с пружинным прижимом одной полумуфты и профиль кулачков в зацеплении углом а. Определить максимальный крутящий момент, передаваемый муфтой при следующих исходных параметрах: коэффициент трения на поверхности кулачков f =0, 1., угол а =300, трением полумуфты по поверхности вала пренебречь. Усилие прижима пружины Р приведено в таблице.
|
|
|
| P, кН | 1, 2 | 1, 3 | 1, 5 | 1, 7 | 2, 3 | 2, 5 | 2, 7 |
Порядок решения:
Pn
PT
P
a
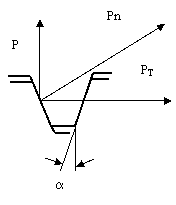 Осевая сила " Р" пружины на полумуфту создаёт окружную силу
Осевая сила " Р" пружины на полумуфту создаёт окружную силу 
Максимальный крутящий момент, передаваемый полумуфтой  где:
где:
 - угол трения на кулачках муфты,
- угол трения на кулачках муфты,
Kn = (0, 8 - 0, 9) - коэффициент неравномерности распределения нагрузки по кулачкам муфты. Результаты решения без учета коэффициента Kn.
|
|
|


