 |
Задача 44. Исходные данные Рв, кN d,мм
|
|
|
|
Задача 44.
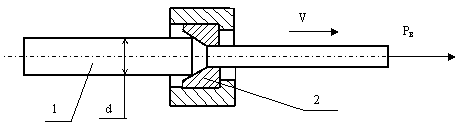
Стальной пруток 1 диаметром «d» протягивается через волоку 2 силой волочения «Рв» со скоростью «V». Определить скорость « отстрела» прутка в момент окончания волочения, принимая допущение, что потенциальная энергия его растяжения переходит в кинетическую энергию движения в направлении волочения. Учесть, что скорость " отстрела" складывается со скоростью волочения.
| Исходные данные | |||||||||
| Рв, кN | |||||||||
| d, мм | |||||||||
| V, м/с | 1, 7 | 1, 7 | 1, 6 | 1, 6 | 1, 5 | 1, 5 | 1, 2 | ||
Порядок решения:
В соответствии с условиями задачи запишем, что потенциальная энергия растяжения прутка силой волочения Рв равна кинетической энергии его движения в момент окончания процесса волочения:
Wp = Wk; или 0, 5Pв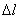 
= 0, 5mV2k. , где 
l = 
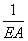Pвl - относительное удлинение прутка при волочении по закону Гука
Е - модуль упругости материала прутка,
А - площадь поперечного сечения материала прутка,
Vк - скорость движения, приобретаемая прутком при снятии нагрузки растяжения.
Решая уравнение, получим: Vk = 1. 27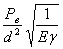 
., где
- удельный вес (плотность) материала прутка равна 7, 85г/cм3.
Полная скорость Vп = V+Vк.
Задача 45
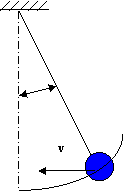Для разрушения старых зданий часто используют передвижной кран, на стреле которого подвешен стальной шар массой M. Oпределить диаметр проволоки каната, на котором подвешивается шар из следующих условий:
- длина каната L=5м.
- число проволок в канате N
-запас прочности каната на разрыв Кз=6
-угол отклонения шара от вертикали 450.
-начальная скорость, сообщаемая шару V=1м/c.
-допускаемое напряжение растяжения материала проволоки каната 600Мпа.
| M, кг | ||||||||||
| N, шт |
|
|
|
Порядок решения:
v
V1
Vг
a
may
mg
x
y
l(1-Cosa)
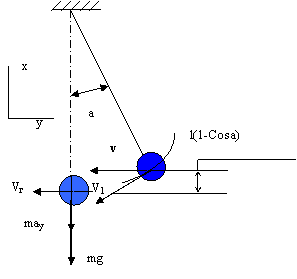Диаметр проволоки определится из уравнения прочности 
, т. е.
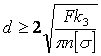. Сила натяжения каната определится из третьего закона Ньютона F= may +mg (сумма проекций на ось Y в вертикальном положении каната).
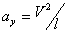- центробежное ускорение,
Vг - горизонтальная (окружная) скорость шара, определяемая из условия сохранения энергии его движения 
; 
,
, 
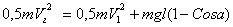
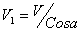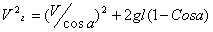где - g ускорение силы тяжести.
Задача 46
Дозатор автоматической линии 1 отсекает один обрабатываемый ролик 2 и со скоростью V отправляет его в желоб 3 на последующую обработку. Углы наклона желоба: а = 150, в = 450. Размер желоба А=200мм. Определить минимальную длину желоба по размеру В, при которой ролик по инерции не выкатится за пределы желоба и вернётся в его центр. Принять скорость V= 0, 5 м/с, коэффициент трения качения между роликом и поверхностью желоба k=0, 0002м. Варианты диаметров ролика приведены в таблице. Задачу решить по одному из вариантов.
| d, мм. |
Порядок решения:
По закону сохранения энергии суммарная энергия ролика в нижней части желоба за вычетом работы сил трения на участке скатывания должна равняться работе подъёма ролика по крутой стенке желоба плюс работа сил трения на участке подъёма, т. е.
;
где 0, 5mV2 - кинетическая энергия ролика в начале движения,
mg A tqa - потенциальная энергия ролика в начале движения,
g - ускорение силы тяжести,
- сила трения при скатывании ролика, d -диаметр ролика,
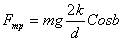- сила трения при подъёме ролика, k - коэффициент трения.
Общее решение уравнений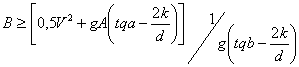 
Задача 47
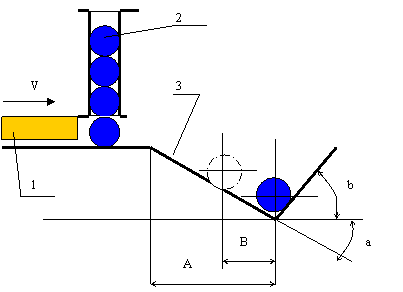Дозатор 1 автоматической линии со скоростью V=0, 5м/с. отсекает один обрабатываемый ролик 2 и отправляет его в желоб 3 на последующую операцию. Углы наклона желоба а=150, b=750. Длина участка желоба А=0, 2м. После соударения со стенкой желоба ролик отскакивает на величину В=0, 02м. Определить контактное напряжение между стенкой желоба и роликом в момент соударения из следующих условий:
|
|
|
Ролик и желоб - стальные. Длина ролика l - 50мм. Коэффициент трения качения между роликом и желобом принять k=0, 0002м. Потерями на деформацию ролика и желоба в момент соударения - пренебречь.
Модуль упругости материала и его плотность принять 2*105 Мпа, и 7, 8г/см3. Расчёт выполнить для одного из диаметров ролика, представленных в таблице.
| D, мм. |
Порядок решения:
Кинетическая энергия вращения колеса должна быть равна работе сил трения на его торможение, т. е. 
, где J - момент инерции колеса, 
- угол по ворота колеса до полной остановки.
Момент трения - 
, где N - нормальная реакция силы веса колеса, равная массе стального колеса m на ускорение силы тяжести - g, f -коэффициент трения между колесом и осью, r - радиус оси.
.
Число оборотов 
.
Конечное решение 
.
|
|
|
