Задача 48. mn- нормальный модуль зацепления равный 3. . Определить угол наклона зуба по делительной окружности. Передача без смещения.

Задача 48

При выполнении лабораторной работы по изучению цилиндрического зубчатого редуктора были замерены следующие параметры косозубой зубчатой передачи:

А- межцентровое расстояние,

z₁- число зубьев шестерни,

z₂- число зубьев колеса.

m_n- нормальный модуль зацепления равный 3.

Определить угол наклона зуба по делительной окружности. Передача без смещения.

Варианты чисел зубьев приведены в таблице. Задачу решить по одному из вариантов.

 

z1
z2

 

Порядок решения:

Межосевое расстояние зубчатой пары ;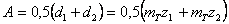

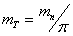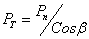- торцевой модуль зацепления. Известно, что нормальный модуль зацепления ; и . Подставляя значения, получим: .

 

Задача 49

При выполнении лабораторной работы по изучению червячных редукторов были измерены следующие параметры некоррегированной червячной пары:

d_a1 – наружный диаметр червяка, z₂- число зубьев червячного колеса, z₁-число витков червяка, m_s- осевой модуль червяка, А – межосевое расстояние.

Определить угол подъёма винтовой линии на червячном колесе , коэффициент диаметра червяка q, передаточное число пары u, диаметр впадин зубьев червячного колеса d_f2. Варианты замеренных данных приведены в таблице.

 

А, мм
dа1
z1
z2
ms

 

Порядок решения:

Известно, что d_a1= d₁+2m. d₁ = qm. . Отсюда, коэффициент диаметра червяка .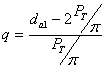

Делительный угол подъёма винтовой линии червяка .

Передаточное число пары .

Диаметр впадин зубьев червячного колеса d_f1= d₂ - 2. 4m = m(z₂ - 2, 4).

 

Задача 50

PT2, V2, T2

N, n₁, T₁

d₂

d₁

P

P

В представленной на рис. фрикционной передаче известны: окружное усилие Р_Т2, окружная скорость V₂= 1, 57м/с, диаметр катка d₂=300мм, передаточное число u= 2, коэффициент трения между катками f = 0, 1., допускаемое давление между катками _n=100Мпа, коэффициент упругого скольжения между валками e=0, 01., коэффициент полезного действия передачи h =0, 98.

Определить силу прижатия катков Р, ширину катков, мощность и частоту вращения привода. Значение окружной силы Р_Т2 приведено в таблице. Задачу решить по одному из вариантов.

 

 

РТ2, Н

 

Порядок решения:

Необходимая сила сжатия катков ;

Ширина катков определится из формулы Герца для контактных напряжений ; . Отсюда .

Здесь Е= Е_пр = 2*10⁵Мпа - модуль упругости материала катков.

Мощность привода N₁=T₁ .

T₁ = P_T2 - крутящий момент на приводе.

Угловая скорость привода .

; .

 

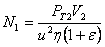Задача 51

 

Р

l

40мм

2000Н

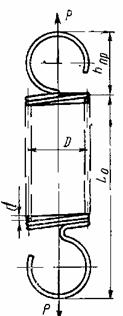
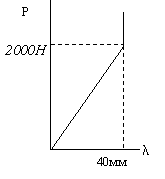Спроектировать цилиндрическую пружину сжатия из проволоки круглого сечения. Характеристика пружины (зависимость осадки l от нагрузки) показана на рисунке. Индекс пружины с= D/d =5; Модуль сдвига материала проволоки G=8*10⁴ МПа;

Допускаемое напряжение на кручение материала проволоки [t]=230МПа; значение поправочного коэффициента k принять из таблицы.

 

C
k	1. 42	1. 31	1. 25	1. 21	1. 18	1. 16	1. 14

 

Порядок решения:

Напряжения в витках пружины вычисляются исходя из момента закручивания проволоки T = P / 0. 5D. Полярный момент сопротивления прутка круглого сечения 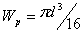. Отсюда напряжение кручения в витках пружины или , где k – коэффициент, учитывающий кривизну витков и влияние поперечной силы в зависимости от индекса пружины с =D/d.

Принимая k= 1. 3, при с=5 (см. таблицу) получим =12мм.

Диаметр пружины D =c*d = 60мм.

Осадка пружины 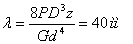, отсюда необходимое число рабочих витков =19, 2.

Полное число витков z_п =z+(1. 5-2) =21

Минимальный зазор между витками пружины при полной нагрузке = 0, 3мм

Шаг пружины при максимальной нагрузке 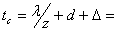14, 4мм.

Длина пружины, сжатой до соприкосновения витков L = (z_п –0. 5)d = 246мм.

Длина ненагруженной пружины L₀ = L+z(t_с - d) = 292мм.

Длина пружины под нагрузкой равной P L₁ = L₀ - l =252мм.

Шаг ненагруженной пружины 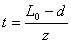=14, 6мм.

Длина проволоки для изготовления пружины =4032мм.

 

 

Задача 52

40мм

Р

l

200Н

Спроектировать цилиндрическую пружину растяжения из проволоки круглого сечения. Характеристика пружины (зависимость осадки l от нагрузки) показана на рисунке. Индекс пружины с= D/d =4; Модуль сдвига материала проволоки G=8*10⁴ МПа;

Допускаемое напряжение на кручение материала проволоки

[t]=240МПа; значение поправочного коэффициента k принять из таблицы.

 

C
k	1. 42	1. 31	1. 25	1. 21	1. 18	1. 16	1. 14

 

Порядок решения:

Напряжения в витках пружины вычисляются исходя из момента закручивания проволоки T = P / 0. 5D. Полярный момент сопротивления прутка круглого сечения 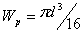. Отсюда напряжение кручения в витках пружины или , где k – коэффициент, учитывающий кривизну витков и влияние поперечной силы в зависимости от индекса пружины с =D/d.

Принимая k= 1. 42, при с=4 (см. таблицу) получим =3, 5мм.

Диаметр пружины D =c*d = 14мм.

Осадка пружины 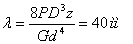, отсюда необходимое число рабочих витков

=109, 5.

Шаг пружины t = d = 3. 5мм.

Полное число витков z_п =z + (0. 5-1)d = 110

Длина пружины в свободном состоянии L₀ =(z_п +1)d = 388. 5мм.

Длина пружины в свободном состоянии с зацепами L = L₀ + 2h_пр =428мм.

Длина зацепа h_пр =(1-2)D =20мм.

Длина пружины при максимальной деформации L_max = L + l = 468мм.

 

Задача 53

Две пружины вставлены одна в другую. До приложения к плите сила Р = 1200Н вторая пружина короче первой на d = 20мм. Найти наибольшие касательные напряжения t_max и вычислить перемещение плиты при следующих условиях:

Средние диаметры пружин равны соответственно D₁ =200мм, D₂ = 100мм. Диаметры проволоки пружин d₁ =20мм, d₂ = 10мм. Число витков z₁ =15,

z₂ =10.

Модуль сдвига материала проволоки G =8*10⁴МПа.

Коэффициент приведения k в зависимости от индекса пружины c= D/d принять по таблице

 

Порядок решения:

Если при рабочей нагрузке плита опустится на величину меньшую или равную d, то сжиматься будет лишь большая пружина, и задача в этом случае статически определима. Если перемещение плиты больше d, то сжимаются обе пружины и система статически не определима. Выясним прежде всего характер работы данной системы: найдём силу Р₀, необходимую для сжатия первой пружины на d =20мм и сопоставим эту силу с заданной.

(cм. решение задачи 52), откуда 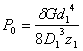= 534Н.

Следовательно при действии силы Р =1200Н нагружены обе пружины. При этом осадка первой пружины l₁ на d больше осадки второй пружины l₂.

Уравнение перемещений l₁ - l₂ =d = 20мм.

Уравнение равновесия сил Р₁ + Р₂ = Р =1200Н, или Р₁ = 1200Н – Р₂.

Совместное решение данных уравнений даёт: Р₁ =800Н, Р₂ = 400Н.

Определяем максимальные касательные напряжения в пружинах

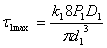= 58МПа, где k₁ = 1. 14 (по таблице при с = 10)

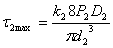=116МПа, где k₂ = 1. 14 (по таблице при с = 10).

Определяем перемещение плиты, равное осадке первой пружины

= 60мм.

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: