 |
2.2. Расчет трансформатора. 2.3. Расчет индуктивности рассеяния. Параметр. Способ расчета
|
|
|
|
2. 2. Расчет трансформатора
На следующем этапе производится настройка вычислительных процедур. Задается начальное и конечное время моделирования, а также допустимые погрешности вычислений. В нашем случае расчеты проводились в диапазоне времени от 0 с до 0, 1 с интервалом в 0, 001 с.
В результате мы можем получить распределение индукции, напряженности магнитного поля и других параметров в трансформаторе.
Посмотрим, как распределяется модуль индукции в середине левого стержня (точка x = 120, y=0).
Рисунок 2. 8. - Распределение модуля индукции магнитного поля в точке x = 120, y=0.
Из графика на рисунке 2. 8 видно, что максимальное значение индукция достигает в момент времени 0, 094 с. Теперь посмотрим, как распределяется индукция во всем магнитопроводе в этот момент времени
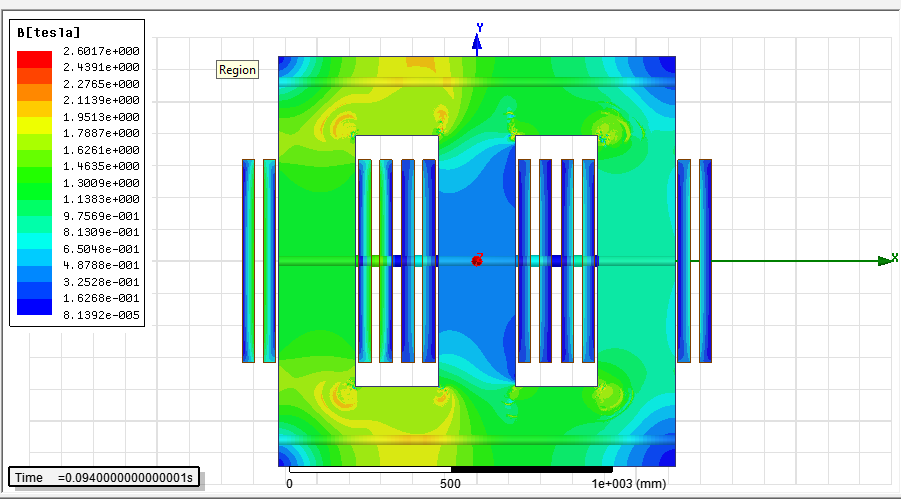
Рисунок 2. 8. - Распределение индукции магнитного поля в момент времени 0, 094 с.
Далее необходимо убедиться, что при изменении параметров напряжения, меняется и распределение индукции, проведем опыт холостого хода.
Рисунок 2. 9 - Распределение индукции магнитного поля в момент времени 0, 094 с (опыт хх).
Одной из основных задач при выполнении электромагнитных расчетов является определение потерь в стали, которые приблизительно соответствуют потерям холостого хода, определяемых при испытаниях трансформаторов.
На рисунке 2. 10 приведены графики изменения во времени потерь в магнитопроводе трансформатора. Эти графики соответствуют графикам изменения напряжения. На графике потери в стали достигают 2, 3 кВт. Значения данных потерь несколько отличаются от [5], в связи с этим для более точного определения потерь необходимо проведение расчетов в трехмерной постановке с детальным учетом конструктивных особенностей магнитопровода.
|
|
|
Рисунок 2. 10 - График изменения потерь Pс от времени
2. 3. Расчет индуктивности рассеяния
Расчет проводим по методике, описанной в [4]. Индуктивность – способность трансформатора накапливать магнитное поле:
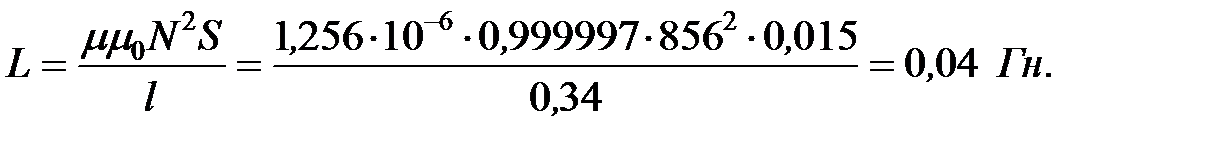
где N – количество витков;
S - площадь поперечного сечения катушки в квадратных метрах;
l = длина катушки в метрах.
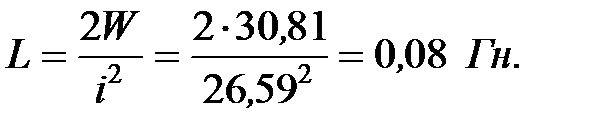
где W – энергия магнитного потока;
I – ток трансформатора.
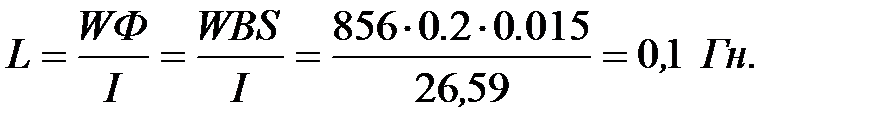
Далее рассчитывает индуктивность рассеяния.
Для расчета индуктивности рассеяния можно воспользоваться формулой, приведенной в [2]:
где w – число витков обмотки;
hн – длина обмотки вдоль направления потока рассеяния;
дu – расстояние между обмотками;
A – толщина обмотки;
lср – средняя длина витка обмотки;
kр – опытный коэффициент, зависящий от типа намотки и данных сердечника.
Так же в работе [3] представлена более простая формула для расчета индуктивности рассеяния:
где Sa/3 – площадь витка, находящегося на расстоянии a/3 от внутреннего витка;
а – радиальный размер обмотки;
Ra/3 – средний (по площади) радиус этого витка. При Ra/3 /a = 2 имеем ka = 0, 04; при Ra/3 /a = 3 – ka = 0, 02; при Ra/3 /a = 4 – ka = 0, 01.
где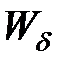 
– энергия рассеяния магнитного потока;
Результаты расчетов внесем в таблицу 2. 1.
Таблица 2. 1
Индуктивности трансформатора
|
Параметр |
Способ расчета | |||||
| По формуле 1 | По формуле 2 | По формуле 3 | По формуле в [2] | По формуле в [3] | По формуле в 3 | |
| Индуктивность L, Гн | 0, 04 | 0, 08 | 0, 1 | |||
| Индуктивность рассеяния, Lσ , Гн | 
| 
| 
| |||
Из таблицы видно, что расчет индуктивностей дает правильный результат, а соответственно можно приступать к выполнению верификации модели..
|
|
|
