 |
2.4. Верификация модели трансформатора
|
|
|
|
Верификацию модели трансформатора предлагается произвести путем сравнения расчетных данных с экспериментальными данными. Так как экспериментальные исследования высоковольтных трансформаторов весьма затруднительны, то предлагается исследовать лабораторные трансформаторы мощностью до 1 кВА (эскиз показан на рисунке 2. 9).
Рисунок 2. 9 - Геометрическая модель лабораторного трансформатора.
Экспериментально индукцию в магнитопроводе трансформатора можно определить с помощью подключения к вторичной обмотке активного сопротивления и емкости. [52] При этом первичная обмотка трансформатора должна быть подключена к переменному напряжению (рисунок 2. 10). Зная значения сопротивления и емкости, а также выходного напряжения, можно определить значение индукции (формула 2. 16 и 2. 17) и сравнить это значение с данными модели Ansys:
(2. 16)
(2. 17)
где R – активное сопротивление, Ом;
C – емкость, Ф.
S – сечение магнитопровода, S = (41, 6/1000) · (36/1000) = 0. 0015 м2;
N – количество витков;
Uвых – выходное напряжение, измеряется вольтметром П2, В;
U – действующее напряжение, измеряется осциллографом, В;
f – частота, f=50 Гц.
Рисунок 2. 10 - Схема измерения индукции в трансформаторе
В цепи на рисунке 2. 10 подключены следующие элементы:
К- кнопка включения, выключения на блоке питания;
П1 – амперметр переменного тока 0 – 1, 2 А;
П2 – вольтметр переменного напряжения 0 - 600 В;
R – активное сопротивление, R = 15 кОм;
C – емкость, С = 9, 5 мкФ.
Для начала необходимо вычислить индуктивность. Для этого необходимо подключить цепь, как на рисунке 2. 11. В этой схеме:
|
|
|
П3 – фазометр, с его помощью измеряется 
.
Цепь подключается к первичной обмотке, у которой 2400 витков. Сопротивление катушки 44, 5 Ом. Для начала замыкается ключ и плавно увеличивается напряжение. Эксперимент выполнен при токе 0, 75 А. После измерения выводится напряжение регулятором, и блок питания отключается кнопкой.
Рисунок 2. 11 – Схема для измерения индуктивности
Индуктивность определяется по формуле:
(2. 18)
где 
- угловая частота, = 314 Рад/с.
Далее подключается схема на рисунке 2. 10. При замыкании ключа К на первичной обмотке возникает переходной процесс нарастания напряжения, который приводит к изменению индукции в исследуемом трансформаторе. Вторичная обмотка (у нёё 25 витков) подключается к сопротивлению и емкости. К емкости параллельно подключается осциллограф для измерения действующего напряжения. Нажав кнопку, увеличиваем значение действующего напряжения до 220 В. Измеряем с помощью П2 значение выходного напряжения.
Вычисляем индукцию по формулам 2. 16 и 2. 17, а результаты измерений сведем в таблицу 2. 2.
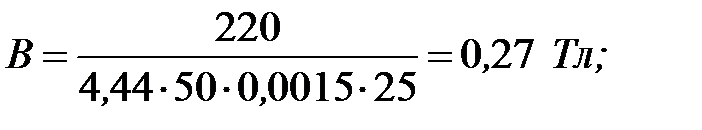
Таблица 2. 2.
Результаты измерений
| Параметр | I, А | Uвых, В | Uдейст, В | cosφ | B по формуле 2. 16, Тл | B по формуле 2. 17, Тл |
| Значение | 0, 75 | 70·10-3 | 0, 19 | 0, 26 | 0, 27 |
Далее выполняется моделирование в пакете Ansys. 3D и 2D модель представлена на рисунках 2. 12 и 2. 13.
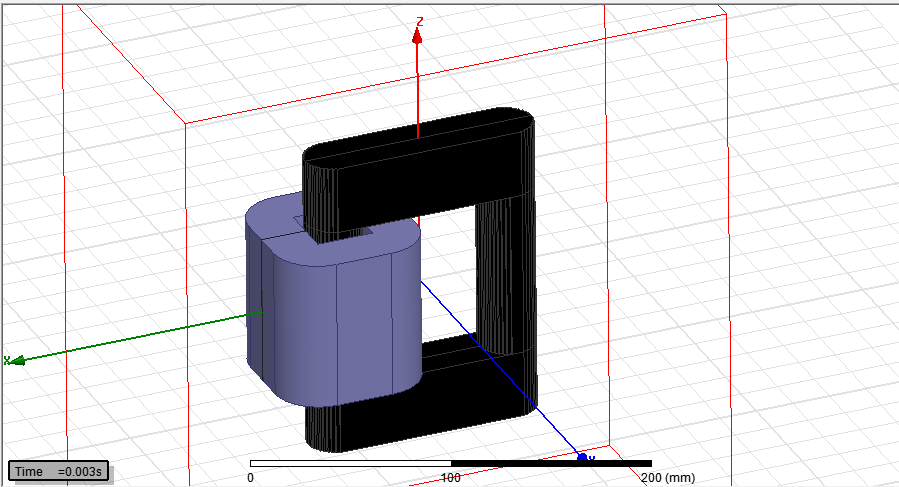
Рисунок 2. 12 - 3D модель лабораторного трансформатора.
Рисунок 2. 13 - 2D модель лабораторного трансформатора.
На первичной обмотке задано экспаненциально изменяющееся напряжение. Функция с экспоненциально увеличивающей амплитудой напряжения используется для устранения бросков магнитного потока и соответственно бросков токов намагничивания Математически эта функциа может быть выражена следующим образом [1, 2]:
(2. 19)
где 
– амплитудное значение напряжения обмоток, В;
|
|
|
=50 Гц – промышленная частота;
– время процесса, с.
График напряжения показан на рисунке 2. 14. Для трансформатора амплитудное значение фазного напряжения – 220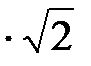 
В.
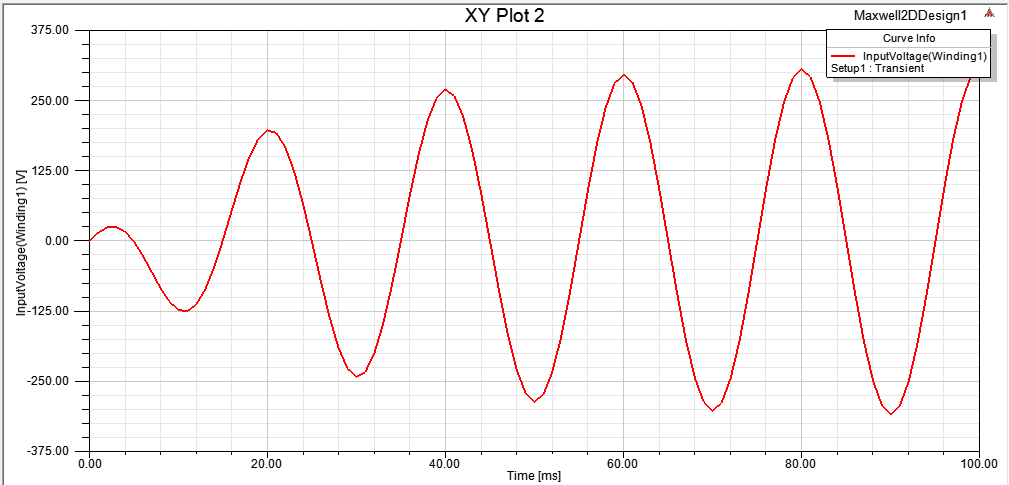
Рисунок 2. 14 - График изменения напряжения на первичной обмотке трансформатора.
Характеристики материалов магнитопровода и обмоток сведены в таблицу 2. 1, а кривая намагничивания стали и удельные потери в стали показаны соответственно на рисунках 2. 15 и 2. 16.
Таблица 2. 1
Характеристики материалов магнитопровода и обмоток
| Название | Материал | μ | σ , См/м | ρ , кг/м3 | Слои | Витки |
| Магнитопровод | Сталь Э1 | по кривой намагничивания | 7872 | - | - | |
| Обмотки | Медь | 0, 999991 | ВН -2400, НН-25 |
Рисунок 2. 15 - Кривая намагничивания стали Э1.
Как правило, кривая намагничивания вводится в Ansys Maxwell в виде таблицы.
Кривая удельных потерь в стали показана на рисунке 2. 16.
Рисунок 2. 16 - Удельные магнитные потери в стали Э1.
Задается начальное и конечное время моделирования, а также допустимые погрешности вычислений. В нашем случае расчеты проводились в диапазоне времени от 0 с до 0, 1 с интервалом в 0, 001 с. После окончания расчета в пакете Ansys Maxwell можно построить полевые графики, т. е. трехмерные или двухмерные графики распределения магнитной индукции, напряженности магнитного поля, плотности электрического тока и других электромагнитных параметров. Кроме этого, в пакете можно построить графики изменения электромагнитных параметров вдоль линий на геометрической модели, а также графики, учитывающие изменение их во времени. В качестве примера на рисунке 2. 17 приведен график распределения магнитной индукции в точке (x=0, 18 м, y=0).
Рисунок 2. 17 - Графики распределения магнитной индукции в точке
(x=0, 18 м, y=0)
Из графика видно, что наибольшее значение индукция достигает в момент времени 0, 094 с. Посмотрим, как распределяется индукции в магнитопроводе в этот момент времени.
Рисунок 2. 18 - График распределения индукции в магнитопроводе в момент времени 0, 094 с.
Из графиков видно, что значение максимальной индукции B = 0, 21 Тл, что отличается приблизительно на 18% от лабораторных расчетов.
|
|
|
|
|
|
