 |
Понятие о случайной функции.
|
|
|
|
СЕВАСТОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
М.М. Гхашим, Т.В.Чернэуцану
СЛУЧАЙНЫЕ ФУНКЦИИ
Учебное пособие
Утверждено
ученым советом института
Севастополь
Гхашим М.М., Т.В.Чернэуцану
Случайные функции: учеб.-метод. пособие. – Севастополь: СевГУ, 2015.
В данном пособии рассмотрены три основных раздела: «», «», «». Каждый из разделов включает в себя основные вопросы теории, разбор типовых примеров, задания для самостоятельной работы с ответами к ним.
предназначено для студентов третьего курса при изучении темы «».
Рецензенты:
к.ф.-м..,
к.т.н, доцент
нк.ф.-м.н доцент
© Издание СевГУ, 2015
ОГЛАВЛЕНИЕ
§ 1. Понятие о случайной функции……………………………………
§ 2. Характеристики случайных функций……………………………
§ 3. Оператор динамической системы……………………………….
§ 4. Линейные преобразования случайных функций………………
§ 5. Стационарные случайные процессы ……………………
§ 6. Спектральное разложение стационарной случайной функции………
§ 7. Эргодическое свойство стационарных случайных функций………….
Решение типовых задач………………………………………………..
Задачи для самостоятельного решения………………………………
ЛИТЕРАТУРА………………………………………………………………
Случайные функции
Понятие о случайной функции.
В курсе теории вероятностей основным предметом исследования были случайные величины, которые характеризовались тем, что в результате опыта принимали некоторое одно, заранее неизвестное, но единственное значение. Т.е., случайные явления изучались как бы в «статике», в каких-то фиксированных постоянных условиях отдельного опыта. Однако на практике часто приходится иметь дело со случайными величинами, непрерывно изменяющимися в процессе опыта. Например, угол упреждения при непрерывном прицеливании по движущейся цели; отклонение траектории управляемого снаряда от теоретической в процессе управления или самонаведения, и т.д. В принципе, любые системы с автоматизированным управлением предъявляют определенные требования к соответствующей теоретической базе – теории автоматического управления. Развитие этой теории невозможно без анализа ошибок, неизбежно сопровождающих процессы управления, которые всегда протекают в условиях непрерывно действующих случайных возмущений или «помех». Эти возмущения по своей природе являются случайными функциями. Итак:
|
|
|
Определение. Случайной функцией X (t) называют функцию неслучайного аргумента t, которая при каждом фиксированном значении аргумента является случайной величиной.
Конкретный вид, принимаемый случайной функцией X (t) в результате опыта, называется реализацией случайной функции.
Пример. Самолет на воздушном курсе имеет теоретически постоянную воздушную скорость V. Фактически его скорость колеблется около этого среднего номинального значения и представляет собой случайную функцию времени. Полет можно рассматривать как опыт, в котором случайная функция V (t) принимает определенную реализацию (Рис.1).
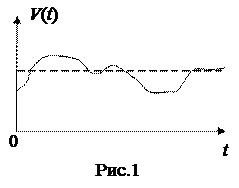 |  | ||
От опыта к опыту вид реализации меняется. Если на самолете установлен самописец, то он в каждом полете запишет новую, отличную от других, реализацию случайной функции. В результате нескольких полетов можно получить семейство реализаций случайной функции V (t) (Рис.2).
На практике встречаются случайные функции, зависящие не от одного аргумента, а от нескольких, например, состояние атмосферы (температура, давление, ветер, осадки). В данном курсе мы будем рассматривать только случайные функции одного аргумента. Так как этим аргументом чаще всего является время, будем обозначать его буквой t. Кроме того, условимся обозначать случайные функции большими буквами (X (t), Y (t), …) в отличие от неслучайных функций (x (t), y (t), …).
|
|
|
Рассмотрим некоторую случайную функцию X (t). Предположим, что над ней произведено n независимых опытов, в результате которых получено n реализаций, которые мы обозначим соответственно номерам опытов x 1(t), x 2(t), …, x n (t). Очевидно, каждая реализация есть обычная (не случайная) функция. Таким образом, в результате каждого опыта случайная функция X (t) превращается в не случайную функцию.
Зафиксируем теперь некоторое значение аргумента t. В этом случае случайная функция X (t) превратится в случайную величину.
Определение. Сечением случайной функции X (t) называют случайную величину, соответствующую фиксированному значению аргумента случайной функции.
Мы видим, что случайная функция совмещает в себе черты случайной величины и функции. В дальнейшем часто будем попеременно рассматривать одну и ту же функцию X (t) то как случайную функцию, то как случайную величину, в зависимости от того, рассматривается ли она на всем диапазоне изменения t или при его фиксированном значении.
Рассмотрим случайную величину X (t) – сечение случайной функции в момент t. Эта случайная величина, очевидно, обладает законом распределения, который в общем случае зависит от t. Обозначим его f (x, t). Функция f (x, t) называется одномерным законом распределения случайной функции X (t).
Очевидно, функция f (x, t) не является полной, исчерпывающей характеристикой случайной функции X (t), т.к. она характеризует только закон распределения X (t) для данного, хотя и произвольного t и не отвечает на вопрос о зависимости случайных величин X (t) при различных t. С этой точки зрения более полной характеристикой случайной функции X (t) является так называемый двумерный закон распределения: f (x 1, x 2; t 1, t 2). Это – закон распределения системы двух случайных величин X (t 1), X (t 2), т.е. двух произвольных сечений случайной функции X (t). Но и эта характеристика в общем случае не является исчерпывающей. Очевидно, теоретически можно неограниченно увеличивать число аргументов и получать все более полную характеристику случайной функции, но оперировать столь громоздкими характеристиками, зависящими от многих аргументов, крайне затруднительно. В пределах данного курса мы вообще не будем пользоваться законами распределения, а ограничимся рассмотрением простейших характеристик случайных функций, аналогичных числовым характеристикам случайных величин.
|
|
|
|
|
|


