Характеристики случайных функций.

В отличие от числовых характеристик случайных величин, представляющих собой числа, характеристики случайных функций представляют собой в общем случае функции.

Рассмотрим сечение случайной функции X (t) при фиксированном t.

Определение. Математическим ожиданием случайной функции X (t) называется неслучайная функция m_x (t) = M [ X (t)], которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.

Свойстваматематического ожидания случайной функции.

1⁰. Математическое ожидание неслучайной функции φ (t) равно самой неслучайной функции:

M [ φ (t)] = φ (t).

2⁰. Неслучайный множитель φ (t) можно выносить за знак математического ожидания

M [ φ (t) · X (t)] = φ (t) · M [ X (t)] = φ (t) · m_x (t).

3⁰. Математическое ожидание суммы двух случайных функций равно сумме их математических ожиданий:

M [ X (t) + Y (t)] = m_x (t) + m_y (t).

Это свойство можно обобщить на любое конечное количество слагаемых:

= .

Следствие. Если X (t) – случайна функция, φ (t) – неслучайная функция, то

M [ X (t) + φ (t)] = m_x (t) + φ (t).

По смыслу математическое ожидание случайной функции есть некоторая средняя функция, около которой различным образом варьируются конкретные реализации случайной функции.

 

Определение. Дисперсией случайной функции X (t) называется неслучайная функция D_x (t), значения которой для каждого t равно дисперсии соответствующего сечения случайной функции:

D_x (t) = D [ X (t)].

Очевидно, что D_x (t) есть неотрицательная функция. Извлекая из нее квадратный корень, получим функцию σ_x (t) – среднее квадратическое отклонение случайной функции:

σ_х(t) = .

Свойства дисперсии случайной функции.

1⁰. Дисперсия неслучайной функции равна нулю:

D [ φ (t)] = 0.

2⁰. Дисперсия суммы случайной функции X (t) и неслучайной функции φ (t) равна дисперсии случайной функции:

D [ X (t) + φ (t)] = D_x (t).

3⁰. Дисперсия произведения случайной функции X (t) на неслучайную функцию φ (t) равна произведению квадрата неслучайного множителя на дисперсию случайной функции:

D [ X (t) · φ (t)] = φ ²(t) · D_x (t).

Дисперсия случайной функции при каждом t характеризует разброс возможных реализаций случайной функции относительно среднего, иными словами, «степень случайности» случайной функции.

Математическое ожидание и дисперсия представляют собой весьма важные характеристики случайной функции, однако для описания основных особенностей случайной функции этих характеристик недостаточно. Рассмотрим две случайные функции X ₁(t) и X ₂(t):

 

Очевидно, что эти случайные функции имеют примерно одинаковые математические ожидания и дисперсии, однако характер этих случайных функций резко различен, и это различие не улавливается ни математическим ожиданием, ни дисперсией. Для описания степени зависимости между сечениями случайной функции, относящимися к различным значениям t, нужна особая характеристика.

Назовем центрированной случайной функцией разность между случайной функцией и ее математическим ожиданием:

= X (t) - m_x (t).

Определение. Корреляционной функцией случайной функции X (t) называют неслучайную функцию K_x (t ₁, t ₂) двух независимых аргументов t ₁ и t ₂, значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений, соответствующих этим же фиксированным значениям аргументов:

K_x (t ₁, t ₂) = .

Свойства корреляционной функции.

1⁰. Симметрия: при перестановке аргументов корреляционная функция не изменяется:

K_x (t ₁, t ₂) = K_x (t ₂, t ₁).

2⁰. Прибавление к случайной функции X (t) неслучайной функции φ (t) не изменяет ее корреляционной функции: если Y (t) = X (t) + φ (t), то

K_у (t ₁, t ₂) = K_x (t ₁, t ₂).

3⁰. При умножении случайной функции X (t) на неслучайную функцию φ (t) ее корреляционная функция умножается на произведение φ (t ₁) · φ (t ₂): если Y (t) = X (t) · φ (t), то

K_у (t ₁, t ₂) = K_x (t ₁, t ₂) · φ (t ₁) · φ (t ₂).

4⁰. Абсолютная величина корреляционной функции не превышает среднего геометрического дисперсий соответствующих сечений:

K_x (t ₁, t ₂) ≤ .

Очевидно, что при равных между собой значениях аргументов t ₁= t ₂ = t корреляционная функция случайной функции равна дисперсии этой функции

K_x (t, t) = D_x (t).

Таким образом, необходимость в дисперсии как отдельной характеристике случайной функции отпадает: в качестве основных характеристик случайной функции достаточно рассматривать ее математическое ожидание и корреляционную функцию.

Вместо корреляционной функции можно пользоваться нормированной корреляционной функцией:

ρ_x (t ₁, t ₂) = = .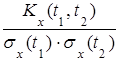

Абсолютная величина нормированной корреляционной функции не превышает единицы: | ρ_x (t ₁, t ₂)| ≤ 1.

 

Вышеуказанные характеристики случайной функции можно определить на основании результатов опыта. Для этого проводится некоторое конечное количество независимых опытов над случайной функцией X (t), и в результате получается конечное количество реализаций X (t). После этого способами, аналогичными статистическим, получают точечные оценки для математического ожидания m_x (t), дисперсии D_x (t) и корреляционной функции K_x (t ₁, t ₂).

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: