Линейные преобразования случайных функций.

Пусть на вход линейной системы с оператором L воздействует случайная функция X (t), причем известны ее характеристики – математическое ожидание m_x (t) и корреляционная функция K_x (t ₁, t ₂). Реакция системы представляет собой случайную функцию Y (t) = L { X (t)}. Требуется найти характеристики случайной функции Y (t) на выходе из системы: m_у (t) и K_у (t ₁, t ₂).

Сначала убедимся, что можно ограничиться решением этой задачи только для однородного оператора L. Действительно, пусть оператор L неоднороден и выражается формулой

L { X (t)} = L ₀{ X (t)} + φ (t),

где L ₀ - линейный однородный оператор, φ (t) – определенная не случайная функция. Тогда

m_у (t) = M [ L ₀{ X (t)}] + φ (t),

т.е. функция φ (t) просто прибавляется к математическому ожиданию случайной функции на выходе линейной системы. Что же касается корреляционной функции, то, как известно, она не изменяется от прибавления к случайной функции неслучайного слагаемого. Поэтому в дальнейшем под «линейными операторами» мы будем подразумевать только линейные однородные операторы.

Решим задачу об определении характеристик на выходе линейной системы сначала для некоторых частных видов линейных операторов.

1⁰. Интеграл от случайной функции.

Дана случайная функция X (t) с математическим ожиданием m_x (t) и корреляционной функцией K_x (t ₁, t ₂). Случайная функция Y (t) связана с X (t) линейным однородным оператором интегрирования:

Y (t) = . (1)

Требуется найти характеристики случайной функции Y (t): m_y (t) и K_y (t ₁, t ₂).

Представим интеграл (1) как предел суммы

Y (t) = = ,

и применим к этому равенству операцию математического ожидания. По теореме о сложении математических ожиданий имеем

m_y (t) = M (Y (t)) = = .

Таким образом, математическое ожидание интеграла от случайной функции равно интегралу от ее математического ожидания.

Найдем корреляционную функцию K_y (t ₁, t ₂). Для этого перейдем к центрированным случайным функциям

= X (t) - m_x (t), = Y (t) - m_y (t).

Нетрудно убедиться, что = .

По определению корреляционной функции

K_y (t ₁, t ₂) = ,

где

= , = .

(здесь применяем известное правило, что под знаком определенного интеграла переменная интегрирования может быть обозначена любой буквой). Тогда

∙ = ∙ .

Так как первый интеграл зависит только от τ ₁, а второй – только от τ ₂, можно записать, что

∙ = .

Применяя к последнему равенству операцию математического ожидания и меняя ее в правой части местами с операцией интегрирования, получим

K_y (t ₁, t ₂) = .

Таким образом, чтобы найти корреляционную функцию интеграла от случайной функции, нужно дважды проинтегрировать корреляционную функцию исходной случайной функции: сначала по одному аргументу, затем – по другому.

2⁰. Производная от случайной функции.

Дана случайная функция X (t) с математическим ожиданием m_x (t) и корреляционной функцией K_x (t ₁, t ₂). Случайная функция Y (t) связана с X (t) линейным однородным оператором дифференцирования:

Y (t) = . (2)

Требуется найти характеристики случайной функции Y (t): m_y (t) и K_y (t ₁, t ₂).

Представим производную (2) в виде предела

Y (t) = .

Применяя к этому равенству операцию математического ожидания, получим

m_y (t) = M (Y (t)) = = ,

т.е. математическое ожидание производной от случайной функции равно производной ее математического ожидания.

Для нахождения корреляционной функции K_y (t ₁, t ₂) перейдем к центрированным случайным функциям и . Очевидно, что

= .

По определению

K_y (t ₁, t ₂) = ,

Подставим вместо и их выражения

K_y (t ₁, t ₂) = .

Представим выражение под знаком математического ожидания в виде второй смешанной частной производной

= .

Мы показали, что знаки математического ожидания и дифференцирования можно менять местами. Следовательно

K_y (t ₁, t ₂) = = = .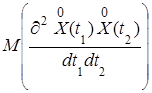

Итак, чтобы найти корреляционную функцию производной, нужно дважды продифференцировать корреляционную функцию исходной случайной функции: сначала по одному аргументу, затем – по другому.

Можно доказать, что правило, полученное для операций интегрирования и дифференцирования, является общим для всех линейных однородных операторов.

Если случайная функция X (t) с математическим ожиданием m_x (t) и корреляционной функцией K_x (t ₁, t ₂) преобразуется линейным оператором L в случайную функцию Y (t) = L { X (t)}, то для нахождения математического ожидания случайной функции Y (t) нужно применить тот же оператор к математическому ожиданию случайной функции X (t):

m_у (t) = L { m_x (t)},

а для нахождения корреляционной функции нужно дважды применить тот же оператор к корреляционной функции случайной функции X (t), сначала по одному аргументу, затем – по другому:

K_у (t ₁, t ₂) = L ^{( t} ₁⁾ L ^{( t} ₂⁾{ K_x (t ₁, t ₂)}.

Во многих практических задачах на выходе линейной системы интересует не корреляционная функция K_у (t ₁, t ₂), а дисперсия D_y (t), характеризующая точность работы системы в условиях наличия случайных возмущений. Дисперсию можно найти, зная корреляционную функцию:

D_y (t) = K_у (t, t).

 

3⁰. Сложение случайных функций.

Во многих задачах практики мы встречаемся с тем, что на вход динамической системы поступает не одна случайная функция X (t), а две или более случайных функций, каждая из которых связана с действием отдельного возмущающего фактора. Возникает задача сложения случайных функций, а точнее – задача определения характеристик суммы по характеристикам слагаемых.

Эта задача является элементарной, если две складываемые функции независимы (точнее, некоррелированы) между собой. В общем же случае для ее решения необходимо знание еще одной характеристики – так называемой взаимной корреляционной функции.

Определение. Взаимной корреляционной функцией случайных функций X (t) и Y (t) называется не случайная функция двух аргументов t ₁ и t ₂, которая при каждой паре значений t ₁, t ₂ равна корреляционному моменту соответствующих сечений случайной функции X (t) и случайной функции Y (t):

R_xy (t ₁, t ₂) = .

Из определения взаимной корреляционной функции вытекает ее следующее свойство:

R_xy (t ₁, t ₂) = R_yх (t ₁, t ₂).

Вместо функции R_xy (t ₁, t ₂) часто пользуются нормированной взаимной корреляционной функцией:

r_xy (t ₁, t ₂) = = .

Если взаимная корреляционная функция равна нулю при всех значениях t ₁ и t ₂, то случайные функции X (t) и Y (t) называются некоррелированными.

Зная математические ожидания и корреляционные функции двух случайных функций X (t) и Y (t), а также их взаимную корреляционную функцию, можно найти характеристики суммы этих двух случайных функций

Z (t) = X (t) + Y (t).

По теореме сложения математических ожиданий

m_z (t) = m_x (t) + m_y (t).

Несложно показать, что

K_z (t ₁, t ₂) = K_x (t ₁, t ₂) + K_y (t ₁, t ₂) + R_xy (t ₁, t ₂) + R_xy (t ₂, t ₁).

В случае, когда случайные функции X (t) и Y (t) некоррелированы, R_xy (t ₁, t ₂) ≡ 0, и последняя формула принимает вид

K_z (t ₁, t ₂) = K_x (t ₁, t ₂) + K_y (t ₁, t ₂).

Полученные формулы могут быть обобщены на случай произвольного числа слагаемых.

Частным случаем сложения случайных функций является сложение случайной функции со случайной величиной.

Рассмотрим случайную функцию X (t) с характеристиками m_x (t) и K_x (t ₁, t ₂) и случайную величину Y с математическим ожиданием m_y и дисперсией D_y. Предположим, что случайная функция X (t) и случайная величина Y некоррелированы, т.е. = 0. Тогда, если рассмотреть случайную функцию Z (t) = X (t) + Y, то очевидно, что

m_z (t) = m_x (t) + m_y.

Несложно также показать, что

K_z (t ₁, t ₂) = K_x (t ₁, t ₂) + D_y.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: