 |
Спектральное разложение стационарной случайной функции.
|
|
|
|
Рассмотрим связь между характером корреляционной функции и структурой соответствующего ей случайного процесса.
Мы будем использовать понятие «спектра», которое широко применяется не только в теории случайных функций, но и в физике и технике. Если какой-либо колебательный процесс представляется в виде суммы гармонических колебаний различных частот (так называемых «гармоник»), то спектром колебательного процесса называют функцию, описывающую распределение амплитуд по различным частотам. Спектр показывает, какого рода колебания преобладают в данном процессе, какова его внутренняя структура. Спектральное описание стационарного случайного процесса будем вводиться аналогично.
Сначала рассмотрим некоторую стационарную случайную функцию  , наблюдаемую на конечном интервале (0, Т). Пусть задана корреляционная функция случайной функции Х (t)
, наблюдаемую на конечном интервале (0, Т). Пусть задана корреляционная функция случайной функции Х (t)
Kx (t, t + τ) = kx (τ).
Мы знаем, что kx (τ) – четная функция, поэтому ее график есть симметричная относительно оси 0Y кривая.
 |
При изменении t 1 и t 2 от 0 до Т аргумент τ изменяется от – Т до Т.
Известно, что четную функцию на интервале (– Т, Т) можно разложить в ряд Фурье, пользуясь только четными (косинусными) гармониками:
kx (τ) =  ,
,
где
ωk = kω 1, ω 1 = 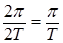 ,
,
а коэффициенты Dk определяются по формулам
D 0 = 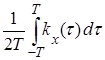 ,
,
Dk =  при k ≠ 0.
при k ≠ 0.
Учитывая, что функции kx (τ) и cos ωk (τ) четные, можно преобразовать выражения для коэффициентов следующим образом:
|
 ,
,
Dk =  при k ≠ 0.
при k ≠ 0.
Можно показать, что в таких обозначениях случайная функция  может быть представлена в виде канонического разложения:
может быть представлена в виде канонического разложения:
 =
=  , (2)
, (2)
где Uk, Vk – некоррелированные случайные величины с математическими ожиданиями, равными нулю, и дисперсиями, одинаковыми для каждой пары случайных величин с одним и тем же индексом k: D (Uk) = D (Vk) = Dk, и дисперсии Dk определяются по формулам (1).
|
|
|
Разложение (2) называется спектральным разложением стационарной случайной функции.
Спектральное разложение изображает стационарную случайную функцию разложенной на гармонические колебания различных частот ω 1, ω 2, …, ω k, …, причем амплитуды этих колебаний являются случайными величинами.
Дисперсия случайной функции  , заданной спектральным разложением (2), определяется по формуле
, заданной спектральным разложением (2), определяется по формуле
Dx =  =
=  =
= 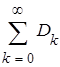 , (3)
, (3)
т.е. дисперсия стационарной случайной функции равна сумме дисперсий всех гармоник ее спектрального разложения.
Формула (3) показывает, что дисперсия функции  известным образом распределена по различным частотам: одним частотам соответствуют б о льшие дисперсии, другим – м е ньшие. Распределение дисперсий по частотам можно проиллюстрировать графически в виде так называемого спектра дисперсий. Для этого по оси абсцисс откладывают частоты ω 0 = 0, ω 1, ω 2, …, ω k, …, а по оси ординат – соответствующие дисперсии.
известным образом распределена по различным частотам: одним частотам соответствуют б о льшие дисперсии, другим – м е ньшие. Распределение дисперсий по частотам можно проиллюстрировать графически в виде так называемого спектра дисперсий. Для этого по оси абсцисс откладывают частоты ω 0 = 0, ω 1, ω 2, …, ω k, …, а по оси ординат – соответствующие дисперсии.

Очевидно, сумма всех ординат построенного таким образом спектра равна дисперсии случайной функции.
Понятно, что чем больший участок времени при построении спектрального разложения мы будем рассматривать, так полнее будут наши сведения о случайной функции. Поэтому естественно попытаться в спектральном разложении попытаться перейти к пределу при T → ∞, и посмотреть, во что при этом обратится спектр случайной функции. При T → ∞ ω 1 =  , поэтому расстояния между частотами ωk, будут неограниченно уменьшаться. При этом дискретный спектр будет приближаться к непрерывному, в котором каждому сколь угодно малому интервалу частот будет соответствовать элементарная дисперсия.
, поэтому расстояния между частотами ωk, будут неограниченно уменьшаться. При этом дискретный спектр будет приближаться к непрерывному, в котором каждому сколь угодно малому интервалу частот будет соответствовать элементарная дисперсия.
Изобразим непрерывный спектр графически. Для этого будем откладывать по оси ординат уже не самую дисперсию Dk, а среднюю плотность дисперсии, т.е. дисперсию, приходящуюся на единицу длины данного интервала частот. Обозначим расстояние между соседними частотами ∆ω, и на каждом отрезке ∆ω, как на основании, построим прямоугольник с площадью Dk. Получим ступенчатую диаграмму, напоминающую по принципу гистограмму статистического распределения.
|
|
|
 |
Высота диаграммы на участке ∆ω, прилежащем к точке ω k, равна
Sx (ωk) =  ,
,
и представляет собой среднюю плотность дисперсии на этом участке. Суммарная площадь всей диаграммы, очевидно, равна дисперсии случайной функции.
Будем неограниченно увеличивать интервал Т. При этом ∆ω → 0, и ступенчатая кривая будет неограниченно приближаться к плавной кривой Sx (ω):
 |
Эта кривая изображает плотность распределения дисперсий по частотам непрерывного спектра, а сама функция Sx (ω) называется спектральной плотностью дисперсии или спектральной плотностью стационарной случайной функции  .
.
Очевидно, площадь, ограниченная кривой Sx (ω), по-прежнему должна равняться дисперсии Dx случайной функции  :
:
Dx =  . (4).
. (4).
Формула (4) есть разложение дисперсии Dx на сумму элементарных слагаемых Sx (ω) dω, каждое из которых представляет собой дисперсию, приходящуюся на элементарный участок частот dω, прилежащий к точке ω.
Таким образом, введена новая дополнительная характеристика стационарного случайного процесса – спектральная плотность, описывающая частотный состав стационарного процесса. Однако она не является самостоятельной – она полностью определяется корреляционной функцией данного процесса. Соответствующая формула, исходящая из разложения корреляционной функции kx (τ) в ряд Фурье на конечном интервале,, выглядит следующим образом:
Sx (ω) =  . (5)
. (5)
При этом сама корреляционная функция также может быть выражена через спектральную плотность:
kx (τ) =  . (6)
. (6)
Формулы типа (5) и (6), связывающие взаимно две функции, называются преобразованиями Фурье.
Заметим, что из общей формулы (6) при τ = 0 получается ранее полученное разложение дисперсии (4).
На практике вместо спектральной плотности Sx (ω) часто пользуются нормированной спектральной плотностью:
|
|
|
sx (ω) =  ,
,
где Dx – дисперсия случайной функции.
Нетрудно убедиться, что нормированная корреляционная функция ρ х(τ) и нормированная спектральная плотность sx (ω) связаны преобразованиями Фурье:
ρ х(τ) =  ,
,
sx (ω) =  .
.
Полагая в первом из этих равенств τ = 0 и учитывая, что ρ х(0) = 1, имеем
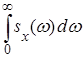 = 1,
= 1,
т.е. полная площадь, ограниченная графиком нормированной спектральной плотности, равна 1.
§ 7. Эргодическое свойство стационарных случайных функций.
Рассмотрим некоторую стационарную случайную функцию X (t) и предположим, что требуется оценить ее характеристики: математическое ожидание mx и корреляционную функцию kx (τ). Эти характеристики, а точнее, их оценки  и
и 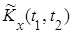 , как уже говорилось, можно получить из опыта, имея известное число реализаций случайной функции X (t). В связи с ограниченностью числа наблюдений функция
, как уже говорилось, можно получить из опыта, имея известное число реализаций случайной функции X (t). В связи с ограниченностью числа наблюдений функция  не будет строго постоянной, ее придется осреднить и заменить некоторым постоянным
не будет строго постоянной, ее придется осреднить и заменить некоторым постоянным 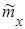 ; аналогично, осредняя значения
; аналогично, осредняя значения 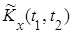 для разных τ = t 2 – t 1, получим корреляционную функцию
для разных τ = t 2 – t 1, получим корреляционную функцию  .
.
Этот метод обработки, очевидно, является довольно сложным и громоздким и к тому же состоит из двух этапов: приближенного определения характеристик случайной функции и также приближенного осреднения этих характеристик. Естественно возникает вопрос - нельзя ли для стационарной случайной функции этот процесс заменить более простым, который заранее базируется на предположении, что математическое ожидание не зависит от времени, а корреляционная функция – от начала отсчета.
Кроме того, возникает вопрос: при обработке наблюдений над стационарной случайной функцией является ли существенно необходимым располагать несколькими реализациями? Поскольку случайный процесс является стационарным и протекает однородно во времени, естественно предположить, что одна-единственная реализация достаточной продолжительности может служить достаточным материалом для получения характеристик случайной функции.
Оказалось, что такая возможность существует, но не для всех случайных процессов. Для примера рассмотрим две стационарные случайные функции, представленные совокупностью своих реализаций.
|
|
|
 |  | ||||||
|
|
Для случайной функции X 1(t) (рис.1) характерна следующая особенность: каждая из ее реализаций обладает одними и теми же характерными признаками: средним значением, вокруг которого происходят колебания и средним размахом этих колебаний. Выберем произвольно одну из таких реализаций и продолжим мысленно опыт, в результате которого она получена, на некоторый участок времени T. Очевидно, что при достаточно большом Т эта одна реализация сможет дать нам достаточно хорошее представление о свойствах случайной функции в целом. В частности, осредняя значения этой реализации вдоль оси абсцисс – по времени, мы должны получить приближенное значение математического ожидания случайной функции; осредняя квадраты отклонений от этого среднего, мы должны получить приближенное значение дисперсии и т.д.
Про такую функцию говорят, что она обладает эргодическим свойством. Эргодическое свойство состоит в том, что каждая отдельная реализация случайной функции является как бы «полномочным представителем» всей совокупности возможных реализаций.
Если мы рассмотрим функцию X 2(t) (рис.2), то очевидно, что для каждой реализации среднее значение свое и существенно отличается от остальных. Поэтому если построить единое среднее значение для всех реализаций, то оно будет существенно отличаться от каждого отдельно взятого.
Если случайная функция X (t) обладает эргодическим свойством, то для нее среднее по времени (на достаточно большом участке наблюдений) приближенно равно среднему по множеству наблюдений. То же будет верно и для X 2(t), X (t) X (t +τ) и т.д. В частности, при достаточно большом Т математическое ожидание mx может быть вычислено по формуле
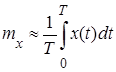 . (1)
. (1)
В этой формуле для простоты опущен знак ~ при характеристике случайной функции, означающий, что мы имеем дело не с самими характеристиками, а с их оценками.
Аналогично можно найти корреляционную функцию kx (τ) при любом τ. Так как
kx (τ) =  ,
,
то вычисляя эту величину при заданном τ, получим
kx (τ) ≈ 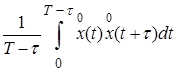 , (2)
, (2)
где 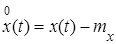 - центрированная реализация. Вычислив интеграл (2) для ряда значений τ, можно приближенно воспроизвести по точкам ход корреляционной функции.
- центрированная реализация. Вычислив интеграл (2) для ряда значений τ, можно приближенно воспроизвести по точкам ход корреляционной функции.
На практике приведенные интегралы обычно заменяют конечными суммами. Это делается следующим образом. Разобьем интервал записи случайной функции на n равных частей длиной ∆ t, и обозначим середины полученных участков t 1, t 2, …, tn.
|
|
|
 |
Представим интеграл (1) как сумму интегралов по элементарным участкам ∆ t и на каждом из них вынесем функцию x (t) из-под знака интеграла средним значением, соответствующим центру интервала - x (ti). Получим приближенно
mx =  =
=  /
/
Аналогично можно вычислить корреляционную функцию для значений τ, равных 0, ∆ t, 2∆ t, … Придадим, например, величине τ значение
τ = 2∆ t =  .
.
Вычислим интеграл (2), деля интервал интегрирования
Т - τ =  =
= 
на n – m равных участков длины ∆ t и вынося на каждом из них функцию  за знак интеграла средним значением. Получим
за знак интеграла средним значением. Получим
 .
.
Вычисление корреляционной функции по приведенной формуле производят для m = 0, 1, 2,…. Последовательно вплоть до таких значений m, при которых корреляционная функция становится практически равной нулю или начинает совершать небольшие нерегулярные колебания около нуля. Общий ход функции kx (τ) воспроизводится по отдельным точкам.

Для того, чтобы характеристики были определены с удовлетворительной точностью, нужно, чтобы число точек n было достаточно велико (порядка 100, а в некоторых случаях и больше). Выбор длины элементарного участка ∆ t определяется характером изменения случайной функции: если она изменяется сравнительно плавно, участок ∆ t можно выбирать больше, чем когда она совершает резкие и частые колебания. Ориентировочно можно рекомендовать выбирать элементарный участок так, чтобы на полный период самой высокочастотной гармоники в составе случайной функции приходилось порядка 5-10 опорных точек.
Решение типовых задач
 1. а) Случайная функция X (t) = (t 3 + 1) U, где U – случайная величина, значения которой принадлежат интервалу (0; 10). Найти реализации функции X (t) в двух испытаниях, в которых величина U приняла значения u 1 = 2, u 2 = 3.
1. а) Случайная функция X (t) = (t 3 + 1) U, где U – случайная величина, значения которой принадлежат интервалу (0; 10). Найти реализации функции X (t) в двух испытаниях, в которых величина U приняла значения u 1 = 2, u 2 = 3.
Решение. Так как реализацией случайной функции X (t) называют неслучайную функцию аргумента t, то при данных значениях величины U соответствующими реализациями случайной функции будут
x 1(t) = 2(t 3 + 1), x 2(t) = 3(t 3 + 1).
б) Случайная функция X (t) = U · sin t, где U – случайная величина.
Найти сечения X (t), соответствующие фиксированным значениям аргумента t 1=  , t 2=
, t 2= 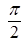 .
.
Решение. Так как сечением случайной функции X (t) называют случайную величину, соответствующую фиксированному значению аргумента, то при данных значениях аргумента соответствующими сечениями будут
X 1 = U ·  =
=  , X 2 = U ·
, X 2 = U ·  = U. ►
= U. ►
 2. Найти математическое ожидание случайной функции X (t) = U · ℮t, где U – случайная величина, причем М (U) = 5.
2. Найти математическое ожидание случайной функции X (t) = U · ℮t, где U – случайная величина, причем М (U) = 5.
Решение. Напомним, что математическим ожиданием случайной функции X (t) называется неслучайная функция mx (t) = M [ X (t)], которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции. Следовательно
mx (t) = M [ X (t)] = M [ U · ℮t ].
Далее, т.к. по свойствам м.о. случайной функции неслучайный множитель можно выносить за знак м.о., получаем
mx (t) = M [ U · ℮t ] = ℮t M (U) = 5 ℮t.
 3. Найти математическое ожидание случайной функции а) X (t) = Ut 2 +2 t +1; б) X (t) = U· sin4 t + V· cos4 t, где U и V – случайные величины, причем М (U) = М (V) = 1.
3. Найти математическое ожидание случайной функции а) X (t) = Ut 2 +2 t +1; б) X (t) = U· sin4 t + V· cos4 t, где U и V – случайные величины, причем М (U) = М (V) = 1.
Решение. Используя свойства м.о. случайной функции, имеем
а) mx (t) = M (Ut 2 +2 t +1) = M (Ut 2) + M (2 t) + M (1) = M (U) t 2+2 t +1 = t 2+2 t +1.
б) mx (t) = M (U· sin4 t + V· cos4 t) = M (U· sin4 t ) + М (V· cos4 t) = M (U) · sin4 t + М (V) · cos4 t = sin4 t + cos4 t. ►
 4. Известна корреляционная функция Kx случайной функции X (t). Найти корреляционную функцию случайной функции Y (t) = X (t) + t 2, используя определения м.о. и корреляционной функции.
4. Известна корреляционная функция Kx случайной функции X (t). Найти корреляционную функцию случайной функции Y (t) = X (t) + t 2, используя определения м.о. и корреляционной функции.
Решение. Найдем м.о. случайной функции Y (t):
mу (t) = M [ Y (t)] = M [ X (t) + t 2] = M [ X (t)] + t 2 = mx (t) + t 2.
Найдем центрированную функцию
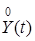 = Y (t) - mу (t) = [ X (t) + t 2] – [ mx (t) + t 2] = X (t) – mx (t) =
= Y (t) - mу (t) = [ X (t) + t 2] – [ mx (t) + t 2] = X (t) – mx (t) =  .
.
Теперь найдем корреляционную функцию
Kу =  =
= 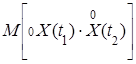 = Kx. ►
= Kx. ►
 5. Известна корреляционная функция Kx случайной функции X (t). Найти корреляционную функцию случайной функции а) Y (t)= X (t)·(t +1); б) Z (t)= C · X (t), где С – константа.
5. Известна корреляционная функция Kx случайной функции X (t). Найти корреляционную функцию случайной функции а) Y (t)= X (t)·(t +1); б) Z (t)= C · X (t), где С – константа.
Решение. а) Найдем м.о. случайной функции Y (t):
mу (t) = M [ Y (t)] = M [ X (t) · (t +1)] = (t +1) · M [ X (t)].
Найдем центрированную функцию
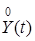 = Y (t)- mу (t)= X (t)·(t +1) - (t +1)· M [ X (t)] = (t +1)·(X (t) - M [ X (t)]) = (t +1)·
= Y (t)- mу (t)= X (t)·(t +1) - (t +1)· M [ X (t)] = (t +1)·(X (t) - M [ X (t)]) = (t +1)·  .
.
Теперь найдем корреляционную функцию
Kу =  =
=  = (t 1+1)(t 2+1) Kx.
= (t 1+1)(t 2+1) Kx.
б) Аналогично случаю а) можно доказать, что
Kу = С 2 Kx. ►
 6. Известна дисперсия Dx (t) случайной функции X (t). Найти дисперсию случайной функции Y (t) = X (t)+2.
6. Известна дисперсия Dx (t) случайной функции X (t). Найти дисперсию случайной функции Y (t) = X (t)+2.
Решение. Прибавление к случайной функции неслучайного слагаемого не изменяет корреляционной функции:
Kу (t 1, t 2) = Kx (t 1, t 2).
Мы знаем, что Kx (t, t) = Dx (t), поэтому
Dу (t) = Kу (t, t) = Kx (t, t) = Dx (t). ►
 7. Известна дисперсия Dx (t) случайной функции X (t). Найти дисперсию случайной функции Y (t) = (t +3) · X (t).
7. Известна дисперсия Dx (t) случайной функции X (t). Найти дисперсию случайной функции Y (t) = (t +3) · X (t).
Решение. Найдем м.о. случайной функции Y (t):
mу (t) = M [ Y (t)] = M [ X (t) · (t +3)] = (t +3) · M [ X (t)].
Найдем центрированную функцию
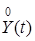 = Y (t)- mу (t)= X (t)·(t +3) - (t +3)· M [ X (t)] = (t +3)·(X (t) - M [ X (t)]) = (t +3)·
= Y (t)- mу (t)= X (t)·(t +3) - (t +3)· M [ X (t)] = (t +3)·(X (t) - M [ X (t)]) = (t +3)·  .
.
Найдем корреляционную функцию
Kу = 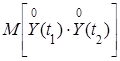 =
=  = (t 1+3)(t 2+3) Kx.
= (t 1+3)(t 2+3) Kx.
Теперь найдем дисперсию
Dу (t) = Kу (t, t) = (t +3)(t +3) Kx (t, t) = (t +3)2 Dx (t). ►

8. Дана случайная функция X (t) = U· cos2 t, где U – случайная величина, причем М (U) = 5, D (U) = 6. Найти математическое ожидание, корреляционную функцию и дисперсию случайной функции X (t).
Решение. Найдем искомое математическое ожидание, вынося неслучайный множитель cos2 t за знак м.о.:
M [ X (t)] = M [ U· cos2 t ] = cos2 t ·M (U) = 5cos2 t.
Найдем центрированную функцию:
 = X (t) - mx (t) = U· cos2 t - 5cos2 t = (U – 5)cos2 t.
= X (t) - mx (t) = U· cos2 t - 5cos2 t = (U – 5)cos2 t.
Найдем искомую корреляционную функцию:
Kx (t 1, t 2) = 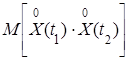 = M {[(U -5) · cos2 t 1] [(U -5) · cos2 t 2]} =
= M {[(U -5) · cos2 t 1] [(U -5) · cos2 t 2]} =
= cos2 t 1 cos2 t 2 M (U -5)2.
Далее, учитывая, что для случайной величины U дисперсия по определению равна D (U) = M [(U - M( (U)]2 = M( (U -5)2, получаем, что M( (U -5)2 = 6. Следовательно, для корреляционной функции окончательно имеем
Kx (t 1, t 2) = 6cos2 t 1 cos2 t 2.
Найдем теперь искомую дисперсию, для чего положим t 1 = t 2 = t:
Dx (t) = Kx (t, t) = 6cos22 t. ►
 9. Задана корреляционная функция Kx (t 1, t 2) = t 1 t 2
9. Задана корреляционная функция Kx (t 1, t 2) = t 1 t 2  . Найти нормированную корреляционную функцию.
. Найти нормированную корреляционную функцию.
Решение. По определению нормированная корреляционная функция
ρx (t 1, t 2) = 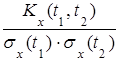 =
=  =
=  .
.
Знак получившегося выражения зависит от того, имеют ли аргументы t 1 и t 2 одинаковые знаки или разные. Знаменатель всегда положителен, поэтому окончательно имеем
ρx (t 1, t 2) = 
 10. Задано математическое ожидание mx (t) = t 2 + 4 случайной функции X (t). Найти математическое ожидание случайной функции Y (t) = tX ´(t) + t 2.
10. Задано математическое ожидание mx (t) = t 2 + 4 случайной функции X (t). Найти математическое ожидание случайной функции Y (t) = tX ´(t) + t 2.
Решение. Математическое ожидание производной от случайной функции равно производной ее математического ожидания. Поэтому
mу (t) = M (Y (t)) = M (tX ´(t) + t 2) = M (tX ´(t)) + M (t 2) =
= t∙M (X ´(t)) + t 2 = t∙ (mx (t))´ + t 2 = t∙ (t 2 + 4)´ + t 2 = 3 t 2. ►
 11. Задана корреляционная функция Kx =
11. Задана корреляционная функция Kx = 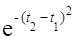 случайной функции X (t). Найти корреляционную функцию от ее производной.
случайной функции X (t). Найти корреляционную функцию от ее производной.
Решение. Чтобы найти корреляционную функцию производной, нужно дважды продифференцировать корреляционную функцию исходной случайной функции, сначала по одному аргументу, затем – по другому.
Найдем частную производную корреляционной функции по первому аргументу
 =
=  .
.
Найдем вторую смешанную производную корреляционной функции
 +
+  =
=
= 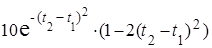 .►
.►

12. Задана случайная функция X (t) = U ℮ 3t cos2 t, где U – случайная величина, причем М (U) = 4, D (U) = 1. Найти математическое ожидание и корреляционную функцию ее производной.
Решение. mх (t) = M (Х (t)) = M (U ℮ 3t cos2 t) = M (U)℮ 3t cos2 t = 4℮ 3t cos2 t.
M (Х´ (t)) = (mх (t))´ = 4(3℮ 3t cos2 t – 2℮ 3t sin2 t) = 4℮ 3t (3cos2 t – 2sin2 t).
Найдем корреляционную функцию исходной случайной функции. Центрированная случайная функция равна
 = X (t) - mx (t) = U ℮ 3t cos2 t - 4℮ 3t cos2 t = (U – 4)℮ 3t cos2 t.
= X (t) - mx (t) = U ℮ 3t cos2 t - 4℮ 3t cos2 t = (U – 4)℮ 3t cos2 t.
Тогда
Kx (t 1, t 2) = 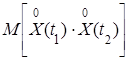 = M {[(U - 4)
= M {[(U - 4)  cos2 t 1] [(U - 4)
cos2 t 1] [(U - 4)  cos2 t 2]} =
cos2 t 2]} =
= 
 cos2 t 1cos2 t 2 M ((U- 4)2)=
cos2 t 1cos2 t 2 M ((U- 4)2)=  cos2 t 1cos2 t 2 D (U)=
cos2 t 1cos2 t 2 D (U)=  cos2 t 1cos2 t 2.
cos2 t 1cos2 t 2.
Найдем частную производную корреляционной функции по первому аргументу
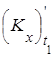 = cos2 t 2
= cos2 t 2  =
=
= cos2 t 2  (3cos2 t 1 – 2sin2 t 1).
(3cos2 t 1 – 2sin2 t 1).
Найдем вторую смешанную производную корреляционной функции
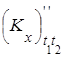 = (3cos2 t 1 – 2sin2 t 1)
= (3cos2 t 1 – 2sin2 t 1)  =
=
=  (3cos2 t 1 – 2sin2 t 1) (3cos2 t 2 – 2sin2 t 2).►
(3cos2 t 1 – 2sin2 t 1) (3cos2 t 2 – 2sin2 t 2).►

13. Задана случайная функция X (t), имеющая математическое ожидание
mx (t) = 3 t 2 + 1. Найти математическое ожидание случайной функции Y (t)=  .
.
Решение. Искомое математическое ожидание
mу (t) =  =
= 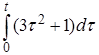 = t 2 + t. ►
= t 2 + t. ►
 14. Найти математическое ожидание интеграла Y (t)=
14. Найти математическое ожидание интеграла Y (t)=  , зная математическое ожидание случайной функции X (t):
, зная математическое ожидание случайной функции X (t):
а) mx (t) = t – cos2 t; б) mx (t) = 4cos2 t.
Решение. а) mу (t) =  =
=  =
=  .
.
б) mу (t) =  =
=  =
= 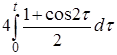 =
=  +
+ 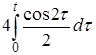 =
=
= 2 t + sin2 t. ►

15. Задана случайная функция X (t) = U ℮ 2t cos3 t, где U – случайная величина, причем М (U) = 5. Найти математическое ожидание интеграла Y (t)=  .
.
Решение. Сначала найдем математическое ожидание самой случайной функции.
mх (t) = M (U ℮ 2t cos3 t) = M (U)℮ 2t cos3 t = 5℮ 2t cos3 t.
Теперь
mу (t) =  = 5
= 5  =
=  =
=
=  ℮ 2t sin3 t -
℮ 2t sin3 t -  =
= 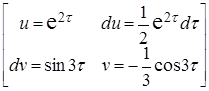 =
=
=  ℮ 2t sin3 t –
℮ 2t sin3 t –  =
=
=  ℮ 2t sin3 t +
℮ 2t sin3 t +  ℮ 2t cos3 t –
℮ 2t cos3 t –  .
.
Получили круговой интеграл, следовательно
5  +
+  =
=  ℮ 2t sin3 t +
℮ 2t sin3 t +  ℮ 2t cos3 t.
℮ 2t cos3 t.
или  =
=  ℮ 2t ( sin3 t +
℮ 2t ( sin3 t + 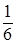 cos3 t).
cos3 t).
Окончательно mу (t) =  ℮ 2t ( sin3 t +
℮ 2t ( sin3 t + 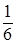 cos3 t).►
cos3 t).►
 16. Найти математическое ожидание интеграла Y (t) =
16. Найти математическое ожидание интеграла Y (t) =  , зная случайную функцию X (t) = U ℮ 3t sin t, где U – случайная величина, причем М (U)=2.
, зная случайную функцию X (t) = U ℮ 3t sin t, где U – случайная величина, причем М (U)=2.
Решение. Найдем математическое ожидание самой случайной функции.
mх (t) = M (U ℮ 3t sin t) = M (U)℮ 3t sin t = 2℮ 3t sin t.
Тогда
mу (t) =  = 2
= 2  =
=  =
=
= – 2℮ 3t cos t +  =
= 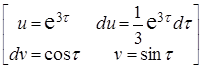 =
=
= – 2℮ 3t cos t +  ℮ 3t sin t –
℮ 3t sin t –  .
.
Имеем  = – ℮ 3t cos t +
= – ℮ 3t cos t +  ℮ 3t sin t.
℮ 3t sin t.
Окончательно mу (t) = –  ℮ 2t cos t +
℮ 2t cos t +  ℮ 2t sin t. ►
℮ 2t sin t. ►

17. Задана случайная функция X (t), имеющая корреляционную функцию
Kx (t 1, t 2) = t 1 t 2. Найти корреляционную функцию интеграла Y (t)=  .
.
Решение. Сначала найдем корреляционную функцию интеграла, которая равна двойному интегралу от заданной корреляционной функции. Следовательно,
Kу (t 1, t 2) = 
 =
= 
 =
= 
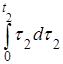 =
=  .
.
Тогда дисперсия Dy (t) = Kу (t, t) =  .►
.►
 18. Задана корреляционная функция Kx (t 1, t 2) =
18. Задана корреляционная функция Kx (t 1, t 2) =  случайной функции X (t). Найти дисперсию интеграла Y (t)=
случайной функции X (t). Найти дисперсию интеграла Y (t)=  .
.
Решение. Найдем корреляционную функцию интеграла
Kу (t 1, t 2) = 
 =
= 
 =
=
= 
 =
= 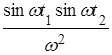 .
.
Тогда дисперсия
Dy (t) = Kу (t, t) =  . ►
. ►
 19. Найти дисперсию интеграла Y (t) =
19. Найти дисперсию интеграла Y (t) =  , зная корреляционную функцию случайной функции X (t):
, зная корреляционную функцию случайной функции X (t):
а) Kx (t 1, t 2) =  ; б) Kx (t 1, t 2) =
; б) Kx (t 1, t 2) =  .
.
Решение. а) Kу (t 1, t 2) = 
 =
= 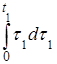
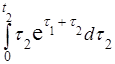 .
.
Вычислим внутренний интеграл, считая τ 1 константой:
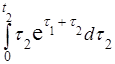 =
=  = t 2
= t 2  –
– 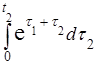 =
=  (t 2 – 1).
(t 2 – 1).
Тогда
Kу (t 1, t 2) = (t 2 – 1) 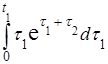 = (t 2 – 1) (t 1 – 1)
= (t 2 – 1) (t 1 – 1)  .
.
Следовательно, дисперсия Dy (t) = Kу (t, t) = (t – 1)2  .
.
б) Kу (t 1, t 2) = 
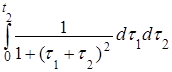 =
=  =
=
=  = t 1 arctg (t 1 + t 2) –
= t 1 arctg (t 1 + t 2) –  == t 1 arctg (t 1 + t 2) –
== t 1 arctg (t 1 + t 2) –  +
+  = (первый интеграл берется заменой переменной) = t 1 arctg (t 1 + t 2) –
= (первый интеграл берется заменой переменной) = t 1 arctg (t 1 + t 2) –  ln|1+(t 1 + t 2)2| + t 2 arctg (t 1 + t 2) =
ln|1+(t 1 + t 2)2| + t 2 arctg (t 1 + t 2) =
= (t 1 + t 2) arctg (t 1 + t 2) –  ln|1+(t 1 + t 2)2|.
ln|1+(t 1 + t 2)2|.
Тогда дисперсия Dy (t) = Kу (t, t) = 2 t arctg 2 t –  ln(1+4 t 2).►
ln(1+4 t 2).►
 20. Найти взаимную корреляционную функцию двух случайных функций X (t) = t 2 U и Y (t) = t 3 U, где U – случайная величина, причем D (U) = 4.
20. Найти взаимную корреляционную функцию двух случайных функций X (t) = t 2 U и Y (t) = t 3 U, где U – случайная величина, причем D (U) = 4.
Решение. Напомним, что взаимная корреляционная функция двух случайных функций вычисляется по формуле
Rxy (t 1, t 2) =  .
.
Найдем математические ожидания наших случайных функций
mx (t) = М (t 2 U) = t 2 mu, mу (t) = М (t 3 U) = t 3 mu.
Найдем центрированные функции
 = X (t) - mx (t) = t 2 U - t 2 mu = t 2(U - mu),
= X (t) - mx (t) = t 2 U - t 2 mu = t 2(U - mu),
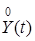 = Y (t) - my (t) = t 3 U - t 3 mu = t 3(U - mu).
= Y (t) - my (t) = t 3 U - t 3 mu = t 3(U - mu).
Найдем взаимную корреляционную функцию
Rxy (t 1, t 2) =  = М {[ t 12(U - mu)][ t 23(U - mu)]} =
= М {[ t 12(U - mu)][ t 23(U - mu)]} =
= t 12 t 23 М (U - mu)2 = t 12 t 23 D (U) = 4 t 12 t 23. ►

21. Найти нормированную взаимную корреляционную функцию случайных функций X (t) = tU и Y (t) = (t + 1) U, где U – случайная величина, причем D (U) = 5.
Решение. Напомним, что нормированная взаимная корреляционная функция ищется по формуле
rxy (t 1, t 2) =  =
=  .
.
Мы знаем следующее свойство дисперсии случайной функции: если случайную функцию умножить на неслучайную, то дисперсия случайной функции умножится на квадрат неслучайной. Поэтому
Dx (t) = D (tU) = t 2 Du = 5 t 2, Dy (t) = D ((t +1) U) = (t + 1)2 Du = 5(t + 1)2.
Найдем центрированные функции
 = X (t) - mx (t) = tU - tmu = t (U - mu),
= X (t) - mx (t) = tU - tmu = t (U - mu),
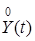 = Y (t) - my (t) = (t + 1) U – (t + 1) mu = (t + 1)(U - mu).
= Y (t) - my (t) = (t + 1) U – (t + 1) mu = (t + 1)(U - mu).
Найдем корреляционную функцию наших случайных функций:
Rxy (t 1, t 2) =  = М {[ t 1(U - mu)][(t 2 + 1)(U - mu)]} =
= М {[ t 1(U - mu)][(t 2 + 1)(U - mu)]} =
= t 1 (t 2 + 1) М (U - mu)2 = t 1 (t 2 + 1) D (U) = 5 t 1 (t 2 + 1).
Теперь найдем нормированную корреляционную функцию:
rxy (t 1, t 2) =  =
=  .
.
В получившемся выражении знаменатель всегда положителен, а знак числителя зависит от знаков слагаемых, поэтому окончательно
rxy (t 1, t 2) = 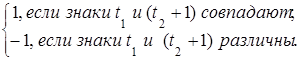 ►
►

22. Известны математические ожидания mx (t) = 2 t + 1 и my (t) = t - 1 и корреляционные функции Kx = t 1 t 2 и Ky =  некоррелированных случайных функций X (t) и Y (t). Найти математическое ожидание и корреляционную функцию случайной функции Z (t) = X (t) + Y (t).
некоррелированных случайных функций X (t) и Y (t). Найти математическое ожидание и корреляционную функцию случайной функции Z (t) = X (t) + Y (t).
Решение. Для любого конечного числа случайных функций математическое ожидание суммы этих случайных функций равно сумме их математических ожиданий, поэтому
mz = mx + my = 2 t + 1 + t – 1 = 3 t.
Корреляционная функция суммы некоррелируемых случайных функций равна сумме корреляционных функций слагаемых, поэтому
Kz = Kx + Ky = t 1 t 2 +  . ►
. ►
 23. Найти математическое ожидание, корреляционную функцию и дисперсию случайной функции X (t) = Ut + Vt 2, где U и V – некоррелированные случайные величины, причем M (U) = 4, M (V) = 7, D (U) = 0,1, D (V) = 2.
23. Найти математическое ожидание, корреляционную функцию и дисперсию случайной функции X (t) = Ut + Vt 2, где U и V – некоррелированные случайные величины, причем M (U) = 4, M (V) = 7, D (U) = 0,1, D (V) = 2.
Решение. Обозначим случайные функции, составляющие X (t) через Y (t)= Ut и Z (t) = Vt 2.
Найдем математическое ожидание случайной функции X (t):
M (X (t)) = M (Y (t)) + M (Z (t)) = M (Ut) + M (Vt 2) = tM (U) + t 2 M (V) = 4 t + 7 t 2 .
По формуле корреляционной функции суммы двух некоррелируемых случайных функций
Kx (t 1, t 2) = Ky (t 1, t 2) + Kz (t 1, t 2) + Ryz (t 1, t 2) + Ryz (t 2, t 1).
Найдем корреляционные функции для Y (t) и Z (t).
Ky (t 1, t 2) =  = М {[ t 1(U - mu)][(t 2(U - mu)]} = t 1 t 2 М (U - mu)2 =
= М {[ t 1(U - mu)][(t 2(U - mu)]} = t 1 t 2 М (U - mu)2 =
= t 1 t 2 D (U) = 0,1 t 1 t 2;
Kz (t 1, t 2) =  = М {[ t 12(V - mv)][(t 22(V - mv)]} = t 12 t 22 М (V - mv)2 =
= М {[ t 12(V - mv)][(t 22(V - mv)]} = t 12 t 22 М (V - mv)2 =
= t 12 t 22 D (V) = 2 t 12 t 22.
Найдем взаимную корреляционную функцию для Y (t) и Z (t).
Ryz (t 1, t 2) =  = М {[ t 1(U - mu)][(t 22(V - mv)]} =
= М {[ t 1(U - mu)][(t 22(V - mv)]} =
= t 1 t 22 М [(U - mu)(V - mv)].
По условию случайные величины U и V – некоррелированные, поэтому их корреляционный момент М [(U - mu)(V - mv)] = 0. Следовательно, Ryz (t 1, t 2) = 0. Аналогично Ryz (t 2, t 1) = 0. Окончательно
Kx (t 1, t 2) = 0,1 t 1 t 2 + 2 t 12 t 22.
Дисперсию находим по формуле
Dx (t) = Kx (t, t) = 0,1 t 2 + 2 t 4. ►
 24. Найти математическое ожидание, корреляционную функцию и дисперсию случайной функции X (t) = U sin t + V cos t, где U и V – некоррелированные случайные величины, причем M (U) = 1, M (V) = 5, D (U) = D (V) = 3.
24. Найти математическое ожидание, корреляционную функцию и дисперсию случайной функции X (t) = U sin t + V cos t, где U и V – некоррелированные случайные величины, причем M (U) = 1, M (V) = 5, D (U) = D (V) = 3.
Решение. Найдем математическое ожидание случайной функции X (t):
M (X (t)) = M (U sin t + V cos t) = M (U sin t) + M (V cos t) = sin tM (U) + cos tM (V) =
= sin t + 5cos t.
Найдем корреляционную функцию
Kx (t 1, t 2) = 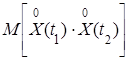 = M {[ U sin t 1+ V cos t 1 - sin t 1 - 5cos t 1] [ U sin t 2 + V cos t 2 -
= M {[ U sin t 1+ V cos t 1 - sin t 1 - 5cos t 1] [ U sin t 2 + V cos t 2 -
- sin t 2 - 5cos t 2]} = M {[(U -1)sin t 1 + (V –5)cos t 1


