Главная | Обратная связь | Поможем написать вашу работу!

Определить коэффициенты опережения и ускорения. Проанализировать полученные результаты.

Год	Мясо, тыс. т	Сахар-песок, тыс. т	Обувь, млн пар	Холодильники, тыс. штук
			15,4
	479,6	864,2	10,1
	546,8	814,1	10,8
	579,6	656,6	11,0
	595,1		11,7

Определить коэффициенты опережения и ускорения. Проанализировать полученные результаты.

Год	Электроэнергия, млрд. кВт∙ч	Нефть, тыс.т	Ткани,	Стиральные машины, тыс. штук
	26,1
	31,0
	31,8
	31,8
	31,8

10.7 Основные фонды народного хозяйства за 10 лет увеличились на 120 %, валовой общественный продукт – в два раза.

Определить коэффициенты опережения и ускорения.

10.8 За 1991 – 2000 г.г. национальный доход страны (в фактически действующих ценах) увеличился в 2 раза. Численность рабочих и служащих в народном хозяйстве – в 1,6 раза.

Определить коэффициенты опережения и ускорения.

10.9 Приведите ряды динамики к общему основанию

Год
выпуск продукции, млн т
число чел

10.10 Приведите ряды динамики к общему основанию

Год
выпуск, млн т
число чел

10.11 Приведите ряды динамики к общему основанию

Год
выпуск продукции, млн т
производительность труда, %

10.12 Приведите смыкание ряда динамики.

Год
продукция по 20 предприятиям, млн руб.
продукция по 24 предприятиям, млн руб.

10.13 Приведите смыкание ряда динамики.

Год
цены на 1.01, тыс. руб.
цены на 1.06, тыс. руб.

10.14 Приведите смыкание ряда динамики.

Год
численность рабочих на 1.01, чел
среднесписочная численность рабочих, чел

10.15 Проведите анализ развития рядов динамики путем выявления общей тенденции.

Год
х
у

10.16 Проведите анализ развития рядов динамики путем выявления общей тенденции.

Год
продукция А, млн руб.
продукция Б, млн руб.

10.17 Проведите анализ развития рядов динамики путем выявления общей тенденции

Год
х
у

10.18 Проведите анализ ряда динамики путем укрупнения периодов.

Дата	У_i	Дата	У_i	Дата	У_i	Дата	У_i	Дата	У_i

10.19 Проведите анализ ряда динамики путем укрупнения периодов.

Месяц	У_i	Месяц	У_i	Месяц	У_i	Месяц	У_i
январь		апрель		июль		октябрь
февраль		май		август		ноябрь
март		июнь		сентябрь		декабрь

10.20 Проведите анализ ряда динамики путем укрупнения периодов.

2005 г.	2006 г.	2007 г.	2008 г.	2009 г.
квартал	У_i	квартал	У_i	квартал	У_i	квартал	У_i	квартал	у
I		I		I		I		I
II		II		II		II		II
III		III		III		III		III
IV		IV		IV		IV		IV

10. 21 Проведите анализ ряда динамики путем определения скользящей средней.

Год
у, т

10.22 Проведите анализ ряда динамики путем определения скользящей средней.

Дата	1.01	1.02	1.03	1.04..	1.05	1.06	1.07	1.08	1.09
у, м

10.23 Проведите анализ ряда динамики путем определения скользящей средней.

Месяц

у, шт.

10.24 Проведите аналитическое выравнивание ряда динамики и определите значение признака в 15 году.

Год	Реализованная продукция, млн руб.	Основные средства, млн руб.	Год	Реализованная продукция, млн руб.	Основные средства, млн руб.

10.25 Проведите аналитическое выравнивание ряда динамики и определите индексы сезонности.

Квартал	2005 г.	2006 г.	2007 г.	2008 г.	2009 г.
I	161,9	150,0	182,1	178,2
II	122,8	103,1	136,8	189,6
III	134,4	114,4	129,1	199,1
IV	144,7	145,8	131,2	187,5

10.26 Проведите аналитическое выравнивание ряда динамики и определите значение признака на 1 августа 9 года.

Год	Выработано электроэнергии, кВт∙ч	Изготовлено, тыс. штук	Год	Выработано электроэнергии, кВт∙ч	Изготовлено, тыс. штук
	26,8			42,6
	26,9			44,6
	29,4			35,1
	27,1			32,7
	32,8			30,8
	40,5			36,1

10.27 Выплавка чугуна на одного работника доменных печей на металлургическом комбинате в 2005 г. составила 6000 т. Тенденция роста производительности труда может быть описана уравнением тренда .

Предполагая, что выявленная тенденция роста производительности труда в ближайшие годы сохранится, определите ожидаемый уровень производительности труда в 2018 г.

10.28 Динамика капиталовложений (тыс. руб.) за 1991 – 2000 г. можно описать уравнением тренда Y = 60 + 2t. Экстраполируя выявленную тенденцию развития, определите объем капиталовложений в 2012 г.

11 ИНДЕКСЫ

Теоретические положения

Под индексом понимается относительный показатель, уровни которого являются экономическими величинами, которые не имеет смысла складывать. Индексы измеряются в тех же единицах измерения, что и относительные величины. При определении индексов применяются следующие обозначения.

Обозначения	Пояснения
i	индивидуальный индекс
I	общий индекс
0	базисный период
1	отчетный период
q	количество продукции в натуральном выражении
p	цена единицы продукции
z	себестоимость единицы продукции
t	трудоемкость изготовления одной штуки
m	расход материалов на одну штуку
T	число человек
S	заработная плата одного человека
pq	товарооборот
zq	общие затраты
tq	отработанное время
ST	фонд заработной платы
mq	общий расход материалов
	производительность труда
	выработка на одного человека

Индексы подразделяются на индивидуальные и общие.

Индивидуальные индексы определяют изменение однородного явления. Обозначаются «i», в правом нижнем углу проставляется индексируемая величина «i_q», иопределяются отношением индексируемой величины в отчетном периоде к индексируемой величине в базисном периоде. Например индивидуальный индекс объема производства в натуральном выражении

i_q = q ₁ / q ₀.

Общие индексы определяют изменение разнородного явления и могут быть образованы двумя методами.

1 метод: Образование на основе введения в индивидуальный индекс соизмерителя. Общие индексы бывают трех видов: переменного состава, постоянного состава и структурных изменений. Например общий индекс цены определяется по соизмерителю – объем выпуска продукции

В индексе переменного состава от периода к периоду изменяется и индексируемая величина и соизмеритель.

В индексе постоянного состава изменяется только индексируемая величина, а соизмеритель находится на уровне базисного периода (Ласпейреса)

, ,

и на уровне отчетного периода (Пааше)

, .

В индексе структурных изменений изменяется только соизмеритель, а индексируемая величина фиксируется на уровне отчетного или базисного периода

, или .

Пример 1. Определить индивидуальные и общие индексы трудоемкости переменного, постоянного состава и структурных изменений.

Вид продукции	Базис	Отчет
количество, шт.	трудоемкость 1 шт., ч	количество, шт	трудоемкость 1 шт., ч
А		0,8		0,7	0,875		4,9	5,6
Б		1,7		1,5	0,88	8,5
В		2,4		2,2	0,92
∑					–	52,5	63,9	70,6

Решение. Индексы определяются по формулам

, ,

Изменение отработанного времени

а) общее определяется как разница между числителем и знаменателем индекса переменного состава

∑ t ₁ q ₁– ∑ t ₀ q ₀ = 63,9 – 52,5 = 11,4 (ч),

б) за счет изменения трудоемкости продукции как разница между числителем и знаменателем индекса постоянного состава

∑ t ₁ q ₁– ∑ t ₀ q ₁ = 63,9 – 70,6 = -6,7 (ч),

в) за счет изменения объема производства как разница между числителем и знаменателем индекса структурных изменений

∑ t ₀ q ₁– ∑ t ₀ q ₀ = 70,6 – 52,5 = 18,1 (ч).

Пример 2. Определить общие индексы переменного состава, постоянного состава и структурных изменений расхода материальных ресурсов.

Вид продукции	Общий расход материалов, т	Индивидуальный индекс расхода материальных ресурсов,
план	отчет
А			0,98
Б			1,07	342,4
В			1,0
∑			–	1012,4

Решение. Индексы определяются по формулам

2 метод: Образование на основе усреднения индексируемой величины по формуле средней арифметической.

Общий индекс себестоимости

, ,

Пример. 3 Определить общие индексы переменного состава, постоянного состава и структурных изменений средней заработной платы.

№ предприятия	Фонд заработной платы, млн руб. s ∙ T	Число человек, Т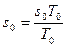
базис	отчет	базис	отчет
				46,2	646,154
				33,125	496,875

∑				–	1627,03

Решение.

Контрольные вопросы

1. Что понимается под индексом?

2. Какие виды индексов существуют?

3. Какова взаимосвязь между индексами?

4. По каким формулам определяются индексы среднего уровня?

Задания

11.1 Какие индексы следует использовать для расчета среднего изменения цен при наличии данных о фактическом товарообороте отчетного периода и об индивидуальных индексах цен по нескольким видам товаров:

а) агрегатной формы;

б) средневзвешенной арифметической;

в) средневзвешенной гармонической;

г) индекс переменного состава;

д) нет правильного ответа.

11.2 Какой индекс следует использовать для определений общего изменения физического объема производства, если известны общие затраты труда на производство в базисном периоде и индивидуальный индекс физического объема производства каждого вида продукции:

а) средневзвешенной арифметической;

б) агрегатной формы;

в) средневзвешенной гармонической;

г) индекс структурных изменений;

д) индекс постоянного состава;

е) нет правильного ответа.

11.3 На основании иже представленных данных определить индивидуальные индексы цен, объема производства и товарооборота.

Месяц	Цена за 1 кг, тыс. руб.	Продано, ц
июнь	5,0	68,2
сентябрь	16,3	445,7
декабрь	19,6	281,1

11.4 На основании ниже представленных данных определить индивидуальные и общие индексы цен; изменение товарооборота общее, за счет изменения цены, за счет изменения объемов продаж.

Продукция	Базисный период	Отчетный период
цена за 1 кг, тыс. руб.	продано, ц	цена за 1 кг, тыс. руб.	продано на сумму, млн руб.
А	2,71	15,8	2,65	3,95
Б	2,84	12,9	2,74	3,42
В	5,2	0,8	5,1	0,33

11.5 На основании иже представленных данных определить индивидуальные и общие индексы себестоимости; изменение затрат на изготовление продукции общее, за счет изменения себестоимости, за счет изменения объемов производства.

Продукция	Базисный период	Отчетный период
себестоимость 1 шт, тыс. руб.	количество шт	себестоимость 1 шт, тыс. руб.	количество шт
А
Б
В

11.6 На основании ниже представленных данных определить индивидуальные и общие индексы трудоемкости; изменение затрат на изготовление продукции общее, за счет изменения трудоемкости, за счет изменения объемов производства.

Продукция	Базисный период	Отчетный период
трудоемкость 1 шт., ч	количество шт.	трудоемкость 1 шт., ч	количество шт.
А	7,2		7,1
Б	12,9		12,0
В	5,3		5,5

11.7 На основании иже представленных данных определить индивидуальные и общие индексы производительности труда

Продукция	Базисный период	Отчетный период
затраты времени на всю продукцию, ч	количество штук	затраты времени на всю продукцию, ч	количество штук
А
Б
В

11.8 На основании иже представленных данных определить индивидуальные и общие индексы выработки.

Продукция	Базисный период	Отчетный период
выпуск продукции, млн руб.	число человек	выпуск продукции, млн руб.	число человек
А
Б
В

11.9 На основании иже представленных данных определить индивидуальные и общие индексы заработной платы; общее изменение фонда заработной платы и влияние на это изменение заработной платы отдельных работников.

Продукция	Базисный период	Отчетный период
фонд заработной платы, млн руб.	число человек	фонд заработной платы, млн руб.	число человек
А
Б
В

11.10 На основании ниже представленных данных определить общие индексы цен; изменение товарооборота общее, за счет изменения цены, за счет изменения объемов продаж.

Продукция	Товарооборот, млн руб.	Изменение цены в отчетном периоде по сравнению с базисным, %
базис	отчет
А			+4
Б			–7
В			без изменений

11.11 На основании иже представленных данных определить общие индексы трудоемкости; изменение отработанного времени: общее, за счет изменения трудоемкости, за счет изменения объемов производства

Продукция	Отработано времени, ч	Изменение трудоемкости в отчетном периоде по сравнению с базисным, %
базис	отчет
А			–4,0
Б			–3,0
В			+2,5

11.12 На основании ниже представленных данных определить общие индексы себестоимости; изменение затрат: общее, за счет изменения себестоимости, за счет изменения объемов производства.

Продукция	Общие затраты, млн руб.	Изменение себестоимости в отчетном периоде по сравнению с базисным, %
базис	отчет
А			–0,7
Б			–2,0
В			–1,6

11.13 На основании ниже представленных данных определить общие индексы производительности труда переменного состава, постоянного состава и структурных изменений.

Продукция	Отработано времени, ч	Изменение производительности труда в отчетном периоде по сравнению с базисным, %
базис	отчет
А			–1,9
Б			–2,3
В			+0,9

11.14 Определить среднее снижение цен на группу товаров, размер экономии покупателей от снижения цен.

Продукция	Старая цена за 1 штуку, тыс. руб.	Новая цена за 1 штуку, тыс. руб.	Товарооборот после снижения цен, млн руб.
А	18,7		1,42
Б	22,0	17,9	2,95
В	31,5	28,6	1,81

11.15 На основании ниже представленных данных определить для однородной продукции общие индексы средней заработной платы; общее изменение средней заработной платы и влияние на это изменение средней заработной платы на отдельных предприятиях и численности работников.

№ предприятия	Базисный период	Отчетный период
фонд зарплаты, млн руб.	число человек	фонд зарплаты, млн руб.	число человек

11.16 На основании ниже представленных данных определить для однородной продукции общие индексы средней выработки; общее изменение средней выработки и влияние на это изменение средней выработки на отдельных предприятиях и численности работников.

№ предприятия	Базисный период	Отчетный период
число человек	выпуск продукции, штук	число человек	выпуск продукции, штук

11.17 На основании иже представленных данных определить для однородной продукции общие индексы средней цены; общее изменение средней цены и влияние на это изменение средней цены на отдельных предприятиях и объемов производства.

№ предприятия	Базисный период	Отчетный период
цена 1 штуки, тыс. руб.	количество штук	цена 1 штуки, тыс. руб.	количество штук
	12,3		12,9
	25,6		25,2
	10,8		9,4

11.18 Определить средний процент снижения цен, если индекс объема выпуска продукции составил 413 %.

Вид продукции	Товарооборот в ценах соответствующего периода, млн руб.
июнь	июль
А	5,1	11,0
Б	0,77	2,16
В	0,72	5,61

11.19 Индекс цен переменного состава равен 1,08, индекс цен постоянного состава 0,94.

Определить индекс структурных изменений и дать интерпретацию полученным результатам.

11,20 Сумма затрат на производство продукции в 2004 г. cоставила 48,3 млн руб. В 2005 г. эти затраты возросли до 50,2 млн руб. Себестоимость единицы продукции в 2004 г. была на 2,5 % выше ее себестоимости в 2005 г. Индекс затрат рабочего времени за рассматриваемой период составил 0,98.

Определить на сколько процентов возросла производительность труда.

11.21 Себестоимость единицы продукции в отчетном периоде снизилась по сравнению с базисным периодом на 1,5 % при неизменных затратах на производство в стоимостном выражении.

Определить, как изменились затраты рабочего времени на производство продукции за этот период, если производительность труда возросла на 0,8 %.

11.22 Производительность труда в отчетном периоде по сравнению с базисным периодом возросла на 3,2 % при увеличении затрат рабочего времени на производство продукции на 1,0 %.

Определить изменение себестоимости единицы продукции, если затраты в стоимостном выражении на единицу продукции остались неизменными.

11.23 В отчетном периоде по сравнению с базисным производство продукции возросло на 650 млн руб.

Определить процент прироста производства продукции в результате повышения производительности труда, если выработка продукции на одного рабочего в отчетном периоде составила 2300 тыс. руб., а численность рабочих возросла на 50 человек.

11.24 В 2010 г. выпуск продукции в стоимостном выражении на предприятии возрос с 375 млн руб. до 420 млн руб. За этот же период численность рабочих увеличилась на 3 %.

Определить процент прироста продукции,полученный вследствии роста производительности труда.

11.25 Среднее снижение цен на группу товаров в июле по сравнению с июнем составило 8,5 %, а в августе по сравнению с июлем – 12 %.

Определить, как изменился объем реализации продукции в августе по сравнению с июнем, если товарооборот за этот период вырос в 2,1 раза (среднее изменение цен определялось с помощью цепных индексов с весами августа).

11.26 Продукция предприятия в базисном периоде в стоимостном выражении составляла 117 млн руб. В отчетном периоде по сравнению с базисном численность рабочих снизилась на 2 %, а производительность труда увеличилась на 6 %.

Определите прирост продукции отчетном периоде по сравнению с базисным.

11.27 За месяц количество реализованных товаров предприятия увеличилось на 8 %, а цены в среднем повысились на 10 %.

Определить, как изменился объем товарооборота за месяц.

11.28 Товарооборот в сентябре по сравнению с августом снизился на 2 %, цены в среднем возросли на 12 %.

Определить, как изменился физический объем товарооборота.

11.29 Количество реализованных товаров за месяц снизилось на 4 %, а объем товарооборота в текущих ценах остался без изменений.

Определить, как изменились в среднем цены на товары.

11.30 Объем производства продукции во втором квартале по сравнению с первым кварталом снизился на 5 %, себестоимость единицы продукции возросла на 4 %.

Определить, как изменились общие затраты на производство продукции.

11.31 Затраты на производство продукции в мае по сравнению с апрелем возросли на 2 %, объем производства возрос на 6 %.

Определить, как изменилась себестоимость единицы продукции.

11.32 Себестоимость единицы продукции в отчетном периоде по сравнению с базисным периодом снизилась на 4,5 %, затраты на производство продукции возросли на 2,6%.

Определить, как изменился объем продукции.

ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ

Теоретические положения

Под выборочным наблюдением понимается такое несплошное наблюдение, при котором обследованию подвергаются единицы совокупности, выбранные случайным образом. Выборочное наблюдение позволяет по выбранной совокупности дать характеристику показателям генеральной совокупности. Выделяют следующие способы выборочного наблюдения:

а) случайная выборка;

б) механическая;

в) типическая;

г) серийная;

д) комбинированная;

е) малая выборка;

ж) метод моментных наблюдений.

Так как наблюдается не вся совокупность, а только ее часть, то возникают ошибки репрезентативности (представительности). К этим ошибкам относятся средняя и предельная ошибки.

Средняя ошибка определяется по формуле

для повторного отбора

для бесповторного отбора

где – генеральная дисперсия;

n – объем выборочной совокупности;

N – объем генеральной совокупности.

При расчетах приближенно можно заменить генеральную дисперсию выборочной.

Предельная ошибка дает возможность определить, в каких пределах находится величина генеральной средней, она определяется по формуле

для повторного отбора

для бесповторного отбора

где t – коэффициент доверия выбирается по таблице;

р – вероятность с которой необходимо получить результаты.

t	p	t	p
	0,683	2,5	0,988
1,5	0,866		0,997
	0,954	3,5	0,999

Зная предельную ошибку и выборочный параметр можно предположить пределы, в которых изменяется величина показателя генеральной совокупности

При проведении выборочного наблюдения часто возникает необходимость в определении численности наблюдения

– для повторного отбора

– для бесповторного отбора

Пример. Определить число наблюдений с вероятностью 0,866, при среднеквадратическом отклонении 2, так чтобы предельная ошибка не превышала 0,8. Объем генеральной совокупности 350 единиц.

Решение. Для вероятности 0,866 t = 1,5

Контрольные вопросы

1.Какие виды выборочного наблюдения существуют?

2.Какие ошибки выборки используются в статистике?

3.Каким образом производится распространение результатов выборки на генеральную совокупность?

4.Как определяется объем выборки?

Задания

12.1 По данным выборочного обследования семейных бюджетов рабочих отрасли оказалось, что среднее число членов семьи 3,2 человека, при µ = 0,0333.

Определить с вероятностью 0,997 среднее число членов семьи.

12.2 Согласно данным выборочного обследования норм выработки на предприятии = 165% при µ =1%.

Определить с вероятностью 0,954 средний процент выполнения норм выработки в генеральной совокупности.

12.3 По данным 2 %-го выборочного обследования (n = 100) средний производственный стаж работы токарей по специальности составляет шесть лет, при коэффициенте вариации V = 30 %.

Определить относительную ошибку выборки для среднего производственного стажа работы токарей с вероятностью 0,954.

12.4 По городской телефонной сети произвели 100 наблюдений и установили, что средняя продолжительность одного разговора 4 мин., при среднеквадратическом отклонении 2 мин.

Определить ошибку выборки с вероятностью 0,954.

12.5 Для определения зольности угля в порядке случайной повторной выборки взято 200 проб. В результате установлена средняя зольность угля 17 %, при среднеквадратическом отклонении 3 %.

С вероятностью 0,954 определите пределы, в которых находится средняя зольность.

12.6 При определении средней продолжительности поездки на работу проводится наблюдение методом случайного бесповторного отбора численности. Численность работающего населения города составляет 170,4 тыс.чел.

Каков должен быть объем выборочной совокупности, чтобы с вероятностью 0,954 ошибка выборки не превышала 5 минут при среднеквадратическом отклонении 25 минут.

12.7 Статистическим управлением города для изучения общественного мнения в порядке механического отбора было опрошено 6400 человек, или 1 % общей численности населения. Из числа опрошенных 3840 человек положительно оценили работу управления.

С вероятностью 0,997 определите пределы, в которых находится доля лиц, положительно оценивающих работу управления.

12.8 На основе данных о хронометраже работы станочников определить среднюю трудоемкость изготовления детали и предельную ошибку этого показателя с вероятностью 0,954, учитывая, что хронометраж проводится в массовом производстве.

Затраты времени на изготовление одной детали, мин.	20 – 21	21 – 22	22 – 23	23 – 24
Число деталей, шт.

12.9 Имеются сведения о генеральной совокупности.

Район	Число единиц совокупности	Максимальный размер доли, %
I
II
III

Определить с вероятностью 0,954 необходимый объем типической выборки, пропорциональной размерам выделенных районов: при повторном отборе; при бесповторном отборе.

12.10 Имеются следующее распределение 100 обследованных ящиков в порядке бесповторного отбора по проценту бракованных изделий в них:

Процент брака, %	1 – 2	2 – 3	3 – 4
Число ящиков, шт.

Можно ли принять всю партию из 1000 ящиков при условии, что процент брака должен быть не больше 2,5 % с вероятностью 0,954?

2.11 В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц;16 ц; 15,5 ц и 14 ц с одного гектара.

Определить с вероятностью 0,954 пределы урожайности области.

12.12 В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225.

С вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.

12.13 С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. человек, в том числе 7 тыс. мужчин и 5 тыс. женщин.

На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет1600.

Определите необходимый объем выборки при вероятности 0,997 и ошибке 5 %.

12.14 В 100 туристических фирмах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора.

Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225?

СПИСОК ЛИТЕРАТУРЫ

1. Адамов, В.Е. Статистика промышленности / В.Е Адамов. – М.: Финансы и статистика, 1987. – 453с.

2. Гришин, А. Статистика: учебное пособие / А. Гришин. – М.: Финансы и статистика, 2003. – 240 с.

3. Громыко, Г. Теория статистика: практикум / Г. Громыко. – М.: ИНФРА-М, 2001. – 160 с.

4. Гусаров, В.М. Теория статистики / В.М. Гусаров. – М.: Аудит: ЮНИТИ, 1998. – 247с.

5. Ефимова, М.Р. Практикум по общей теории статистики: учебное пособие / М.Р. Ефимова, О.И. Ганченко, Е.В. Петрова – М.: Финансы и статистика, 2002. – 336 с.

6. Дуглас, Л. Основы статистики для деловых людей и экономистов / Л. Дуглас, Мейсон Роберт Д. – Burr Ridqe ets: Jrwin, 1994.

7. Макарова, Н.В. Статистика в Excel: учебное пособие / Н.В. Макарова, В. Трофимец. – М.: Финансы и статистика, 2002. – 368 с

8. Практикум по теории статистики / под ред. проф. Р. А. Шмойловой. – М.: Финансы и статистика, 1998. – 534 с.

9. Статистика: учебное пособие / под ред. В. Ионина. – М.: ИНФРА-М, 2002. – 384 с

10. Статистика: учебное пособие / Л.П. Харченко [и др.]. – М.: ИНФРА-М, 2001. – 384 с.

11. Теория статистики / под ред. проф. Р. А. Шмойловой. – М.: Финансы и статистика, 2002. – 557 с.

12. Ходанович Г. В. Статистика: методическое пособие по выполнению лабораторных работ с использованием вычислительной техники для студентов экономических специальностей / Г.В. Ходанович, С.В. Шевченко. – Минск.: «ВУЗ-ЮНИТИ», 2003. – 70 с.

13. Экономическая статистика: учебное пособие / под ред. Ю. Иванова. – М.: ИНФРА-М, 2002. – 480 с.

⇐ Предыдущая 13 14 15 16 171819 20 21 22 Следующая ⇒

Воспользуйтесь поиском по сайту: