 |
Cтатистика предприятий отрасли 15 глава
|
|
|
|
Среднеквадратическое отклонение признака определяется по формуле
Коэффициент осцилляцииопределяется по формуле
Коэффициент вариации по линейному отклонению (относительное линейное отклонение) определяется по формуле
Коэффициент вариации по среднеквадратическому отклонению определяется по формуле
Пример для интервальных рядов. Определите средний разряд, моду, медиану показатели вариации средней арифметической.
| Выпуск продукции, млн руб. | Число предприятий
|
|
|
|
|
|
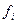
| 1 – 3 | 10,59 | |||||
| 3 – 5 | 12,24 | |||||
| 5 – 7 | 5,64 | |||||
| 7 – 9 | 17,29 | |||||
| ∑ | – | 45,76 |
Решение. Для сгруппированных данных средняя арифметическая определяется
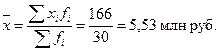
В интервальных рядах распределения мода определяется по формуле
=
= 
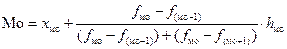Для определения медианы в интервальном ряду воспользуемся формулой
.
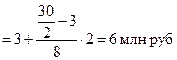Размах вариации признака определяется по формуле
R = х макс– х мин = 9 – 1 = 8 млн руб.
Среднее линейное отклонениепризнака от средней арифметической определяется по формуле
Дисперсия признака определяется
Среднеквадратическое отклонение признака определяется по формуле
Коэффициент осцилляции определяется по формуле
Коэффициент вариации по линейному отклонению (относительное линейное отклонение) определяется по формуле
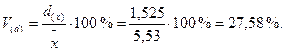
Коэффициент вариации по среднеквадратическому отклонению определяется по формуле
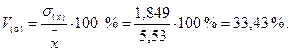
Контрольные вопросы
1. Какие виды средних величин существуют?
2. По каким формулам определяются простые средние?
|
|
|
3. Методы определения степенной средней.
4. Какие показатели вариации средней арифметической рассчитываются?
Задания
6.1 Графически ряды распределения изображаются при помощи:
а) полигона;
б) гистограммы;
в) огивы;
г) кумуляты;
д) нет правильного ответа.
6.2 Средняя является величиной, типичной для качественно однородной совокупности:
а) да; б) нет; в) иногда.
6.3 Средняя является величиной, типичной для любой совокупности:
а) да; б) нет; в) иногда.
6.4 Если все индивидуальные значения признака уменьшить на 20 единиц, то средняя:
а) уменьшится на 20 единиц;
б) уменьшится в 20 раз;
в) не изменится;
г) изменение средней предсказать нельзя;
д) нет правильного ответа.
6.5 Если все значения признака уменьшить в 10 раз, то средняя арифметическая:
а) не изменится;
б) уменьшится в 10 раз;
в) уменьшится в 100 раз;
г) уменьшится на 10;
д) предсказать изменение средней арифметической нельзя;
е) нет правильного ответа.
6.6 Если все значения признака уменьшить в 10 раз, то дисперсия
а) не изменится;
б) уменьшится в 10 раз;
в) уменьшится в 100 раз;
г) уменьшится на 10;
д) предсказать изменение дисперсии нельзя;
е) нет правильного ответа.
6.7 Для определения среднего значения признака, индивидуальные значения которого выражены обратными показателями,
следует применить формулу:
а) средней кубической;
б) средней гармонической;
в) средней арифметической;
г) средней геометрической;
д) средней квадратической.
6.8 Определить средний тарифный разряд, моду, медиану, показатели вариации средней арифметической. Построить графики ряда распределения.
| № рабочего | Тарифный разряд | № рабочего | Тарифный разряд | № рабочего | Тарифный разряд |
6.9 Определите средний стаж, моду, медиану, показатели вариации средней арифметической. Построить графики ряда распределения.
|
|
|
| № рабочего | Стаж, лет | № рабочего | Стаж, лет | № рабочего | Стаж, лет |
6.10 Определить средний размер обуви, моду, медиану, показатели вариации средней арифметической. Построить графики ряда распределения.
| № | Размер обуви | № | Размер обуви | № | Размер обуви |
6.11 Определить среднее число детей в семье, моду, медиану, показатели вариации средней. Построить графики ряда распределения.
| Число детей в семье | Число семей | Число детей в семье | Число семей |
| ∑ | ∑ |
6.12 Определить среднее количество обслуживаемых станков, моду, медиану, показатели вариации средней арифметической. Построить графики ряда распределения.
| Количество обслуживаемых станков | Число рабочих | Количество обслуживаемых станков | Число рабочих |
| ∑ | ∑ |
6.13 Определить среднюю арифметическую, моду, медиану, показатели вариации средней арифметической. Построить графики ряда распределения и определить графически моду и медиану.
| Выпуск продукции, млн руб. | Число предприятий |
| до 150 | |
| 150 – 300 | |
| 300 – 450 | |
| 450 – 600 | |
| 600 – 750 | |
| 750 – 900 | |
| ∑ |
6.14 Определить среднюю арифметическую, моду, медиану, показатели вариации средней арифметической. Построить графики ряда распределения и определить графически моду и медиану.
| Коэффициент использования | Число предприятий |
| 0,5 – 0,6 | |
| 0,6 – 0,7 | |
| 0,7 – 0,8 | |
| 0,8 – 0,9 | |
| 0,9 – 1,0 | |
| 1,0 – 1,1 | |
| ∑ |
6.15 Определить среднюю арифметическую методом моментов, моду, медиану, показатели вариации средней арифметической. Построить графики ряда распределения и определить графически моду и медиану.
|
|
|
| Возраст, лет | Число предприятий |
| до 25 | |
| 25 – 35 | |
| 35 – 45 | |
| 45 – 55 | |
| 55 – 65 | |
| 65 – 75 | |
| ∑ |
6.16 Определить среднюю арифметическую методом моментов, моду, медиану, показатели вариации средней арифметической, начальные и центральные моменты первых пяти порядков.
| Заработная плата, тыс. руб. | Число человек |
| до 200 | |
| 200 – 450 | |
| 450 – 550 | |
| 550 – 700 | |
| 700 – 800 | |
| 800 – 1000 | |
| ∑ |
6.17 Определить среднюю арифметическую методом моментов, моду, медиану, показатели вариации средней арифметической, начальные и центральные моменты первых пяти порядков.
| Основные средства, млн руб. | Число предприятий |
| до 20 | |
| 20 – 50 | |
| 50 – 150 | |
| 150 – 400 | |
| 400 – 600 | |
| 600 – 950 | |
| ∑ |
6.18 Определить среднюю арифметическую методом моментов, моду, медиану, показатели вариации средней арифметической, начальные и центральные моменты первых пяти порядков.
| Средняя заработная плата, тыс. руб. | Число предприятий |
| до – 400 | |
| 400 – 800 | |
| 800 – 1200 | |
| 1200 – 1600 | |
| 1600 – 2000 | |
| ∑ |
6.19 Определить дисперсию, если средняя величина признака равна 260 млн руб., а коэффициент вариации 29 %.
6.20 Определить дисперсию, если средняя величина признака равна 15 млн руб., а коэффициент вариации 37 %.
6.21 Дисперсия признака равна 360000 тыс. руб.2, коэффициент вариации составляет 50 %.
Определить среднее значение признака.
6.22 Средняя величина признака равна 15чел., а дисперсия 174 чел.2.
Определить коэффициент вариации.
6.23 Определить внутригрупповые, межгрупповую и общую дисперсии.
| Заработная плата, тыс. руб. | Число человек | ||
| бригада № 1 | бригада № 2 | бригада № 3 | |
| до 500 | – | ||
| 500 – 600 | |||
| 600 – 700 | |||
| 700 – 800 | |||
| 800 – 900 | – | ||
| 900 – 1000 | – | – | |
| ∑ |
6.24 Определить внутригрупповые, межгрупповую и общую дисперсии.
| Выпуск продукции, млн руб. | Число предприятий | ||
| район А | район Б | район В | |
| до 50 | – | ||
| 50 – 150 | – | ||
| 150 – 250 | |||
| 250 – 350 | |||
| 350 – 450 | |||
| 450 – 550 | – | ||
| ∑ |
|
|
|
6.25 Определить внутригрупповые, межгрупповую и общую дисперсии.
| Разряд рабочих | Число человек | ||
| бригада № 1 | бригада № 2 | бригада № 3 | |
| ∑ |
6.26 Определить внутригрупповые, межгрупповую и общую дисперсии.
| Основные средства, млн руб. | Число человек | ||
| предприятие № 1 | предприятие № 2 | предприятие № 3 | |
| До 2 | |||
| 2 – 10 | |||
| 10 – 50 | |||
| 50 – 150 | |||
| 150 – 500 | |||
| 500 – 2000 | |||
| ∑ |
6.27 Средний квадрат отклонений вариантов признака от произвольной величины 30 равен 136, средняя арифметическая равна 20.
Определить коэффициент вариации.
7ХАРАКТЕРИСТИКА ФОРМЫ РАСПРЕДЕЛЕНИЯ
Теоретические положения
Наиболее распространенными для анализа кривой нормального распределения являются показатели асимметрии и эксцесса.
Асимметрия характеризует симметричность кривой нормального распределения относительно средней арифметической и рассчитывается по формуле
где µ 
– центральный момент третьего порядка, который определяется по формуле
.
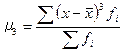При сравнении нескольких рядов по их симметричности можно воспользоваться формулами:
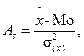или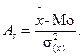 
Оценка существенности асимметрии проводится с помощью среднеквадратической ошибки.
,
где n – число наблюдений.
В случае 
, асимметрия существенна.
Показатель эксцесса отражает форму вершины кривой нормального распределения и рассчитывается по формуле
где µ 
– центральный момент четвертого порядка, который определяется по формуле
.
Средняя квадратическая ошибка эксцесса рассчитывается по формуле
.
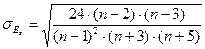Для проверки гипотезы необходимо определить теоретические частоты по формуле плотности нормального распределения
.
Для удобства расчета теоретических частот обозначим:
через коэффициент доверия – 
через функцию – 
.
Для характеристики состоятельности гипотезы о принадлежности кривой типу кривых нормального распределения определяем критерий ХИ – квадрат «
» по формуле
.
Расчетное значение критерия сравнивается с табличным, если оно меньше или равно табличному значению, значит, гипотеза о принадлежности кривой нормальному распределению верна.
При отсутствии табличного значения можно оценить гипотезу по критерию Романовского
,
где m – число групп.
Если С > 3,то гипотеза о принадлежности кривой нормальному распределению верна.
Пример. Определить параметры кривой нормального распределения
|
|
|
|
|
| 
| 
| 
| 
|
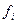
| -34,2959 | 65,1605 | ||||
| -4,374 | 3,9366 | ||||
| 0,01 | 0,001 | ||||
| 6,655 | 7,3205 | ||||
| 37,044 | 77,7924 | ||||
| ∑ | 5,0391 | 154,211 |
Определяем среднюю арифметическую
Среднеквадратическое отклонениеопределяется по формуле
.
Центральный эмпирический момент третьего порядка определяем по формуле
.
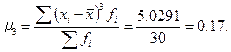
Т.к. асимметрия > 0, то кривая имеет правостороннюю асимметрию по отношению к средней арифметической.
.
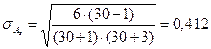Так как отношение коэффициента асимметрии по модулю к средней квадратической ошибке меньше 3, то асимметрия не существенна, и ее наличие обусловливается влиянием случайных факторов (0,087 / 0,412 = 0,21 < 3).
Так как 
– 0,89 < 0, то вершина плотности распределения является плоской.
Соответствие данного распределения нормальному проверяем по критерию хи – квадрат (Х 2)
.
Для расчета критерия хи – квадрат необходимо определить теоретические частоты по формуле кривой нормального распределения
|
|
| 
|
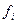
| f теор | 
|
| – 1,52 | 0,125998 | 1,33 | |||
| – 0,72 | 0,308667 | 0,5 | |||
| 0,08 | 0,397957 | ||||
| 0,88 | 0,271582 | 0,57 | |||
| 1,68 | 0,097540 | ||||
| – | – | 4,4 |
Теоретические частоты,исходя из функции плотности распределения, определяются по формуле
.
Если суммы теоретических и эмпирических частот равны, то расчеты верны. Теоретические частоты наносятся на график эмпирических частот.
Проверим соответствие кривой типу кривых нормального распределения по критерию «Романовского»
.
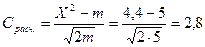Так как расчетное значение критерия «Романовского» меньше 3, то кривая не соответствует типу кривых нормального распределения.
Контрольные вопросы
1. Какие виды форм распределения существуют?
2. По каким показателям оценивается симметричное и асимметричное распределение?
3. Какой показатель характеризует форму вершины кривой нормального распределения и его характеристики?
4. По какой формуле определяются теоретические частоты?
5. Критерий хи – квадрат и его анализ.
6. Критерий Романовского и его применение.
Задания
7.1 Если фактическое значение хи – квадрат больше теоретического хи – квадрат то критерий признает отклонения (f – f т,):
а) существенными;
б) существенность отклонений остается не доказанной;
в) несущественным;
г) предсказать невозможно;
д) нет правильного ответа.
7.2 Если фактическое значение хи – квадрат меньше теоретического хи – квадрат, то критерий признает отклонения (f – f т):
а) существенными;
б) несущественным;
в) существенность отклонений остается недоказанной;
г) предсказать невозможно.
7.3 Величина хи – квадрат может быть рассчитана на основании:
а) величины признака;
б) теоретических и эмпирических частот;
в) вероятностей и эмпирических частот;
г) предсказать невозможно.
7.4 Провести анализ на соответствие ряда распределения нормальному распределению.
| Стаж работы, лет | Число человек | Стаж работы, лет | Число человек | Стаж работы, лет | Число человек |
| до2 | 8 – 11 | 17 – 20 | |||
| 2 – 5 | 11 – 14 | 20 – 23 | |||
| 5 – 8 | 14 – 17 | 23 – 26 |
7.5 Провести анализ на соответствие ряда распределения нормальному распределению.
| Разряд | Число человек | Разряд | Число человек | Разряд | Число человек |
7.6 Провести анализ на соответствие ряда распределения нормальному распределению.
|
|
|
