 |
Cтатистика предприятий отрасли 17 глава
|
|
|
|
Средний уровень рассчитывается по формуле
Средний абсолютный прирост цепной
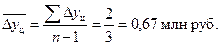
Средний абсолютный прирост базисный
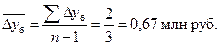
Средний цепной темп роста
.
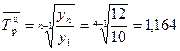Средний базисный темп роста
Средний цепной темп прироста
= 
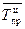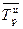– 1 = 1,164 – 1 = 0,164.
Средний базисный темп прироста
= 
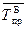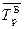– 1 = 1,059 – 1 = 0,059.
Контрольные вопросы
1. Какие основные элементы ряда динамики?
2. Как определяются абсолютные показатели ряда динамики?
3. Как определяются относительные показатели ряда динамики?
4. Как определяются средние показатели ряда динамики?
5. Каким образом взаимосвязаны показатели ряда динамики?
Задания
9.1 Моментным рядом динамики является:
а) выпуск продукции на предприятии за каждый день месяца;
б) остатки товаров на складе по данным ежегодных инвентаризаций;
в) средняя заработная плата рабочих;
г) тарифный разряд;
д) нет правильного ответа.
9.2 Периодическим рядом динамики является:
а) распределение рабочих по затратам времени на одну деталь;
б) производительность труда на промышленном предприятии за каждый месяц;
в) выпуск продукции за месяц;
г) нет правильного ответа.
9.3 Среднегодовой темп роста рассчитывается как:
а) средняя арифметическая;
б) средняя геометрическая;
в) средняя хронологическая;
г) средняя гармоническая;
д) среднеквадратическая;
е) нет правильного ответа.
9.4 Определить показатели ряда динамики.
| Год | Основные средства, млн руб. | Год | Основные средства, млн руб. | Год | Основные средства, млн руб. |
9.5 Определить показатели ряда динамики.
|
|
|
| Год | Число человек | Год | Число человек | Год | Число человек |
9.6 Определить показатели ряда динамики.
| Год | ||||||
| число человек | ||||||
| выпуск продукции, млн руб. |
9.7 Определить показатели ряда динамики.
| Год | |||||||||
| сталь, млн т | |||||||||
| часы, тыс. шт |
9.8 Определить показатели ряда динамики за шесть месяцев.
| Дата | 1.01 | 1.02. | 1.03 | 1.04 | 1.05 | 1.06 | 1.07 |
| продукция, млн руб. |
9.9 Определить показатели ряда динамики за шесть месяцев.
| Дата | 1.01 | 1.02. | 1.03 | 1.04 | 1.05 | 1.06 | 1.07 |
| продукция, млн руб. |
910 Определить показатели ряда динамики за год.
| Дата | 1.01 | 1.04 | 1.07 | 1.10 | 31,12 |
| уi, шт |
9.11 Определить показатели ряда динамики за два месяца.
| Дата | 1.01 | 10.01. | 20.01 | 1.02. | 10.02 | 20.02. | 1.03. |
| уi, м2 | 12,5 | 14,1 | 15,3 | 14,9 | 15,0 | 14,8 | 15,2 |
9.12 Определить показатели ряда динамики и заполнить таблицу.
| Год | Выпуск продукции, млн руб. | Базисные показатели динамики | ||
| абсолютный прирост, млн руб. | темп роста, % | темп прироста, % | ||
| 55,1 | ||||
| 2,8 | ||||
| 110,3 | ||||
| 17,1 | ||||
| 121,1 | ||||
| 13,5 | ||||
| 25,4 | ||||
9.13 Определить показатели ряда динамики и заполнить таблицу.
| Год | Выпуск продукции, шт | Базисные показатели динамики | ||
| абсолютный прирост, шт | темп роста | темп прироста | ||
| 1,08 | ||||
| 0,16 | ||||
| 1,32 | ||||
| 0,32 | ||||
| 1,48 | ||||
| 0,56 | ||||
| 1,6 |
|
|
|
9.14 Определить показатели ряда динамик и заполнить таблицу.
| Год | Выпуск продукции, млн руб. | Цепные показатели ряда динамики | Абсолютное значение одного процента прироста | ||
| абсолютный прирост, млн руб. | темп роста, % | темп прироста, % | |||
| – | – | – | – | ||
| 5,30 | |||||
| 5,8 |
9.15 Определить показатели ряда динамики и заполнить таблицу.
| Год | Уi млн руб. | Цепные показатели ряда динамики | Абсолютное значение одного процента прироста | ||
| абсолютный прирост, млн руб. | темп роста | темп прироста | |||
| – | – | – | – | ||
| 1,03 | |||||
| 0,012 | |||||
| 1,025 | |||||
| 0,014 | |||||
| 1,032 |
9.16 Товарооборот за 1996 – 2000 г. увеличился в 1,4 раза, а за 1996 – 2005 г. – в 1,9 раза. Определить темп роста товарооборота за 2000 – 2005 г.
9.17 Капитальные вложения за 1996 – 2000 г. увеличились в 1,4 раза, за 1996 – 2005 г. в 1,96 раза. Определить темп роста капитальных вложений за 2000 – 2005 г.
9.18 Производство продукции в 2000 г. составило 55 млн.руб., а в 2005 г. – в 1,4 раза больше.
Определить абсолютный прирост за указанный период.
9.19 Определить среднегодовой темп роста за 2001 – 2005 г., если среднегодовой темп роста за 2001 – 2002 г. составил 1,02; а в 2003 – 2005 г. составил 1,05.
9.20 Определить среднегодовой темп роста выпуска продукции за рассматриваемый период.
| Год | |||||
| Выпуск продукции, млн руб. |
9.21 Объем продукции предприятия в 1998 г. был выше ее объема в 1997 г. на 2 %; в 1999 г. он составил 105 % по отношению к объему 1998 г., а в 2000 г. был в 1,2 раза больше объема 1997 г. В 2001 г. предприятие выпустило продукции на сумму 25 млн руб., что на 10% больше, чем в 2000 г., а в 2002 г. – на сумму 30 млн руб. и в 2003 г. – на сумму 37 млн руб.
Определить цепные и базисные темпы роста, абсолютные уровни производства за все годы, среднегодовые темпы роста и прироста.
|
|
|
9.22 Определить среднегодовые темпы роста и прироста производительности труда, если в 1995 г. производительность труда составила 134 %, а в 2011 г. – 166 %.
АНАЛИЗ РЯДОВ ДИНАМИКИ
Теоретические положения
Анализ рядов динамики в зависимости от целей исследования проводится следующими методами.
1) Сравнение рядов динамики применяется при одновременном анализе двух и более рядов. Он показывает во сколько раз быстрее растут уровни одного ряда по сравнению с другим. Для анализа определяются коэффициенты:
а) опережения
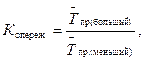
где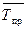 
- средний темп прироста.
б) ускорения
Пример 1. Определить коэффициенты опережения и ускорения.
| Год | Выпуск продукции, млн руб. | Заработная плата, млн руб. |
| 0,400 | ||
| 0,450 | ||
| 0,520 | ||
| 0,550 |
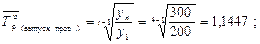
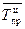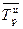= – 1 = 1,1447 – 1 = 0,1447;
;
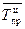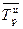= – 1 = 1,112 – 1 =0,112.
Коэффициент опережения
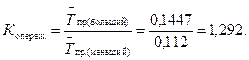
Коэффициент ускорения
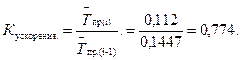
На основании расчетов видно, что выпуск продукции развивается более высокими темпами, чем заработная плата, так как коэффициент опережения больше единицы, а ускорения меньше.
2) Приведение рядов динамики к общему основанию применяется в том случае, если сравниваются только относительные показатели. Для этого определяются базисные показателе к единому году сравнения.
Пример 2. Проанализировать ряды динами методом приведения их к общему основанию.
| Год | Вид продукции | Базисные темпы роста | ||
| А, млн руб. | Б, млн руб. | А | Б | |
| 5 / 5 = 1,0 | 10 / 10 = 1,0 | |||
| 8 / 5 = 1,6 | 11 / 10 = 1,1 | |||
| 12 / 5 = 2,4 | 12 / 10 = 1,2 |
Ряд продукции А развивается более высокими темпами.
3) Смыкание рядов динамики применяется в том случае, если уровни за одни годы не сопоставимы с уровнями за другие. Несопоставимость уровней может возникнуть из–за территориальных изменений, реорганизации управления, переходом к другим единицам измерения. Для ликвидации несопоставимости используют коэффициент пересчета
,
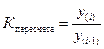где уi – значение признака по новым условиям;
|
|
|
у(i -1) – значения признака по старым условиям.
Пример 3. Провести смыкание ряда динамики.
| Год | ||||||||
| Выпуск продукции в ценах 2001 г., млн руб. | 52 / 1.5 = = 34.7 | 56 / 1.5 = =37.3 | 58 / 1.5 = =38.7 | |||||
| Выпуск продукции в ценах 2005 г., млн руб. | 21 ∙ 1,5 = = 31,5 | 25 ∙ 1,5 = = 37,5 | 24 ∙ 1,5 = = 36 | 26 ∙ 1,5 = == 39 |
Решение. Коэффициент пересчета
4) Выявления общей тенденции в стремлении ряда к росту, стабильности, снижению. Кроме анализа тенденции изучается характер динамики. Под характером динамики понимается тенденция изменения показателей динами: абсолютного прироста, темпов роста, темпов прироста.
5) Приемом укрупнения периодов пользуются в том случае, если необходимо выявить общую тенденцию динамики, переходя от суточных уровней к декадным; от декадных к месячным; от месячных к квартальным и так далее.
6) Анализ рядов динамики при помощи скользящей средней применяется в том случае, если по исходным данным трудно предположить вид зависимости.
Скользящая средняя определяется из нечетного количества первых признаков ряда динамики, затем из такого же количества признаков ряда начиная со второго определяется вторая средняя, затем третья начиная и третьего и так далее. Полученные значения наносятся на график фактических значений, они проставляются на против среднего года из выбранных.
Пример 4. Определить скользящую среднюю.
| Год | Основные средства, млн руб. | Скользящая трехлетняя средняя, млн руб. |
| – | ||
| (50 + 52 + 60) / 3 = 54 | ||
| (52 + 60 + 67) / 3 = 59,7 | ||
| (60 + 67 + 64) / 3 = 63,7 | ||
| (67 + 64 + 67) / 3 = 66 | ||
| (64 + 67 + 70) / 3 = 67 | ||
| – |
7. Аналитическое выравнивание ряда динамики
Прогнозирование параметров рядов динамики выполняется с помощью трендовых моделей.
Линейное уравнение зависимости между признаками имеет вид
y = a + b t.
Система нормальных уравнений для нахождения параметров уравнения
,
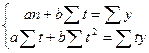где n – число периодов;
t – условное время;
y – значения уровней ряда динамики;
а, b – параметры уравнения.
При использовании для прогнозирования модели параболы второго порядка, уравнение которой имеет вид
.
Система нормальных уравнений для нахождения параметров уравнения «а», «b» и «с» будет иметь вид
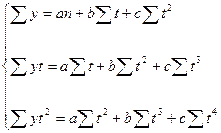
Пример 5. Определить параметры уравнения зависимости выпуска продукции от времени.
Решение: Строим график
Предполагаем прямолинейную зависимость между месяцем и признаком.
Подставляем в систему нормальных уравнений значения, и определяем коэффициенты «а» и «b».
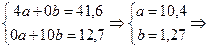. y теор = 10,4 + 1,27 t.
|
|
|
| Месяц | Выпуск, млн руб. | ∑ t | ∑ 
| ∑ 
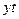
| y теор |
| Я | 7,3 | –2 | –14,6 | 7,86 | |
| Ф | 9,5 | –1 | –9,5 | 9,13 | |
| М | 12,8 | +1 | 12,8 | 11,67 | |
| А | 12,0 | +2 | 24,0 | 12,94 | |
| 41,6 | 12,7 | 41,6 |
Подставляем в уравнение время «t» и получаем теоретические значения игрека. Так как сумма теоретических и эмпирических значений равна, то параметры уравнения рассчитаны верно.
Функция Фурье для определения зависимости в рядах динамики применяется в том случае, если признаки имеют сезонные колебания. В качестве аналитической формы сезонной волны применяется уравнение
,
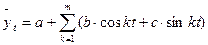где k – порядковый номер гармоники, степень точности тригонометрического многочлена;
t –время;
m – количество гармоник.
Пример 6. Определить параметры функции Фурье.
| Квартал | 
| t, градусы | cos t | sin t | y∙ cos t | y∙ sin t |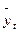 
|
|
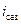
| I | 6,25 | 0,625 | ||||||
| II | 23,75 | 1,188 | ||||||
| III | –1 | –30 | 26,25 | 0,875 | ||||
| IV | –1 | –5 | 8,75 | 1,750 | ||||
| ∑ | – | – | – | –20 | +15 | 1,000 |
Решение. Строим график
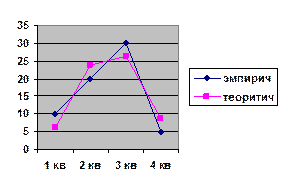
Предполагаем вид зависимости функцию Фурье. При k = 1 уравнение ряда Фурье примет вид
,
;
;
.
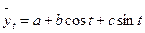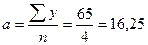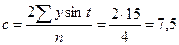Уравнение примет вид
.
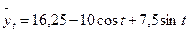Подставляя в формулу вместо «t» его значения, находим «».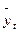
Так как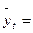 
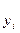, то параметры уравнения рассчитаны верно.
Индекс сезонности показывает отклонение тренда от фактических значений и определяется по формуле
.
Контрольные вопросы
1. Какие применяются методы анализа рядов динамики?
2. Корреляционный анализ в рядах динамики.
3. Как проводится интерполяция и экстраполяция в рядах динамики?
Задания
10.1 При сравнении динамики взаимосвязанных показателей применяются приемы:
а) приведение рядов к одному основанию;
б) смыкание рядов;
в) сложение рядов;
г) сглаживание рядов;
д) группировки;
е) нет правильного ответа.
10.2 С целью приведения несопоставимых уровней ряда динамики к сопоставимому виду применяются приемы:
а) приведение рядов динамики к одному основанию;
б) смыкание рядов динамики;
в) сложение рядов;
г) сглаживание рядов;
д) группировки.
10.3 Для измерения сезонных колебаний используется:
а) показатель вариации;
б) индекс сезонности;
в) средний темп роста;
г) абсолютный прирост;
д) темп прироста.
10.4 Индекс сезонности можно рассчитать как отношение фактического уровня за месяц к
а) среднемесячному уровню за год;
б) теоретическому уровню за тот же месяц;
в) теоритичесому уровню за предыдущий месяц;
г) начальному уровню ряда;
д) конечному уровню ряда.
|
|
|
