 |
Элементы математической статистики и математического анализа используемые в управлении качеством.
|
|
|
|
Случайные величины
Случайной называют величину, которая в результате опыта может принимать различные значения. Например, при бросании игральной кости каждому бросанию (исходу опыта) соответствует единственное число от 1 до 6, причем каждый раз разное. То есть каждому исходу опыта 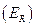 поставлено в соответствии единственное число
поставлено в соответствии единственное число 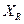 , которое называется значением случайной величины
, которое называется значением случайной величины 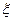 на исходе опыта
на исходе опыта 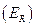 . Результаты могут быть представлены в виде первоначальной таблицы.
. Результаты могут быть представлены в виде первоначальной таблицы.
| Исход опыта Е | 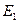
| 
| 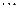
| 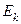
|
Значение случайной величины 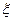
| 
| 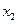
| 
| 
|
Например, при бросании игральной кости первоначальная таблица может иметь вид
| Номер опыта | |||||
Значение случайной величины 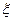
|
Случайные величины принято обозначать греческими буквами ξ (кси), η (эта) и т.д.
Для моделирования случайных величин необходимо знать их характеристики. Полной характеристикой случайной величины является их закон распределения, задаваемый в дифференциальной или интегральной форме.
Дискретная случайная величина X однозначно определяется, если задана область возможных значений xi и распределение вероятностей P(xi) всех возможных значений величины внутри этой области. Функция P(xi) называется законом распределения случайной дискретной величины.
| Значение случайной величины | x1 | x2 | x3 | xn |
| Вероятность события | P(x1) | P(x2) | P(x3) | P(xn) |
Непрерывная случайная величина X однозначно определяется, если задана область возможных значений и плотность вероятности  внутри этой области.
внутри этой области.
Плотность вероятности  есть предел отношения вероятности того, что величина имеет значение в интервале (x, x+Δx) к величине интервала Δx, когда Δx стремится к нулю.
есть предел отношения вероятности того, что величина имеет значение в интервале (x, x+Δx) к величине интервала Δx, когда Δx стремится к нулю.
|
|
|
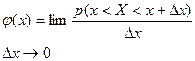

Рис. 1 Теоретическая кривая распределения (закон распределения).
Кривая, являющаяся графическим изображением плотности вероятности  называется теоретической кривой распределения или дифференциальным законом распределения или просто законом распределения.
называется теоретической кривой распределения или дифференциальным законом распределения или просто законом распределения.
Непрерывная случайная величина может быть задана функцией распределения F(x). Функция распределения F(x) равна вероятности того, что в результате опыта случайная величина приняла значение меньше x.
F(x)=P(ξ<x)
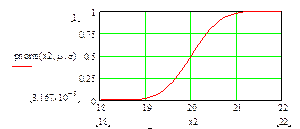
Рис.2 Функция распределения.
Функция распределения и плотность вероятности связаны соотношениями:

Выборочный метод
Совокупность всех возможных элементов, обладающих изучаемым признаком, называется генеральной совокупностью.
Часть элементов, отобранных из генеральной совокупности для исследования, называется выборочной совокупностью или выборкой.
Основными характеристиками генеральной совокупности являются плотность вероятности  , математическое ожидание M(x) и дисперсия
, математическое ожидание M(x) и дисперсия 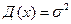 .
.
Математическое ожидание или теоретическое среднее значение является характеристикой центра группирования случайных величин:  .
.
Дисперсия характеризует рассеивание случайной величины: 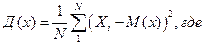 N – объем генеральной совокупности.
N – объем генеральной совокупности.
Основными характеристиками выборки являются эмпирическое распределение, заданное в виде таблицы распределения, гистограммы или полинома распределения, среднее значение (среднее арифметическое) 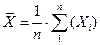 и дисперсия
и дисперсия 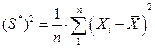 , где n- объем выборки (количество элементов в выборке).
, где n- объем выборки (количество элементов в выборке).
Для построения таблицы распределения диапазон изменения случайной величины разбивается на равные интервалы и определяется частота попадания случайной величины в интервал.
Графическое представление таблицы распределения в виде ломаного графика называется полигон распределения. В виде столбчатого графика – гистограмма. Полигон распределения и гистограмма являются приближённой оценкой плотности распределения.
|
|
|
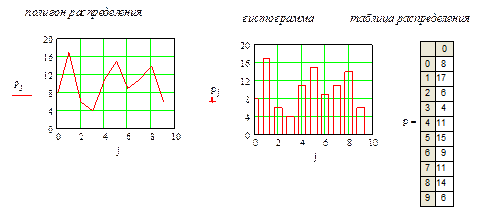
Задачей выборочного метода является оценка параметров генеральной совокупности с помощью выборочных характеристик.
Однако  - являются приближенной оценкой истинного значения
- являются приближенной оценкой истинного значения  и
и 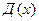 .
.
Оценки генеральной совокупности должны быть несмещенные, состоятельные и эффективные.
Оценка называется:
- несмещенной, если 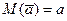
- состоятельной, если 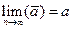
- эффективный, если 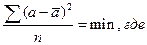
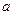 - параметр генеральной совокупности.
- параметр генеральной совокупности.
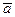 - оценка генеральной совокупности.
- оценка генеральной совокупности.
Несмещенной, состоятельной и эффективной оценкой  является
является 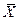 , однако
, однако 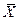 является случайной.
является случайной.
 приближенно оценивается числом.
приближенно оценивается числом.
Степень приближения можно оценивать с помощью доверительного интервала.
Доверительным интервалом параметра генеральной совокупности называется интервал, охватывающий этот параметр с заданной вероятностью.
Для математического ожидания доверительный интервал имеет вид:
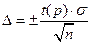 (при известной дисперсии
(при известной дисперсии  ), где
), где
 - квантиль нормального распределения.
- квантиль нормального распределения.
Квантилем, отвечающим заданному уровню вероятности P, называется такое значение  , при котором функция распределения принимает значение P.
, при котором функция распределения принимает значение P.
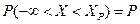 или
или 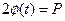 при
при 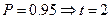 ,
, 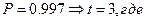
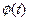 - функция Лапласа.
- функция Лапласа.
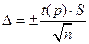 (при неизвестной дисперсии
(при неизвестной дисперсии  ), где
), где
 - критерии Стьюдента с
- критерии Стьюдента с 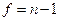 степенями свободы.
степенями свободы.
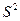 - эмпирическая дисперсия (выборочная).
- эмпирическая дисперсия (выборочная).
Число степеней свободы равно числу обрабатываемых результатов измерений уменьшаемому на число связывающих их линейных соотношений.
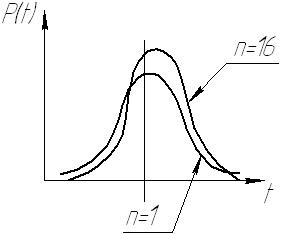
Функция распределения случайно величины t называется законом распределением Стьюдента
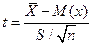
Законы распределения t не зависит от  или от
или от  , и представляет собой семейство законов.
, и представляет собой семейство законов.
 - является смещенной оценкой
- является смещенной оценкой 
Несмещенной, состоятельной и эффективной оценкой  является эмпирическая выборочная дисперсия
является эмпирическая выборочная дисперсия 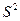
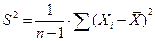

Доверительный интервал для среднего квадратического отклонения равен
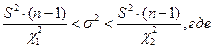
 - хи - квадрат распределения.(верхняя и нижняя граница);
- хи - квадрат распределения.(верхняя и нижняя граница);
При заданном числе опытов  и надежности
и надежности 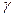 значение хи-квадрата находится по таблицам с числом степеней свободы
значение хи-квадрата находится по таблицам с числом степеней свободы  и достоверностью
и достоверностью 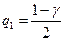 и
и 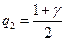 .
.
Иногда граница задается таблично.
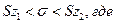
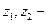 коэффициент, зависящий от
коэффициент, зависящий от  и
и 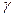 .
.
Понятие хи-квадрат распределения: 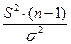 .
.
Если n – большое, то  .
.
Объем выборки
1. При известной 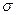 :
: 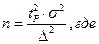
|
|
|
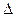 - допустимая погрешность определения среднего.
- допустимая погрешность определения среднего.
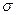 - среднее квадратичное отклонение.
- среднее квадратичное отклонение.
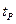 - квантиль нормального распределения.
- квантиль нормального распределения.
При 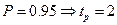 ,
, 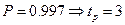 .
.
2. При неизвестной 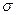 :
:
 (при
(при 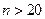 ), где
), где 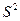 - выборочная дисперсия.
- выборочная дисперсия.
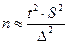 (при
(при 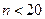 ), где
), где 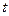 - квантиль распределения Стьюдента.
- квантиль распределения Стьюдента.
Если 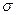 не задано, то производят предварительную выборку с
не задано, то производят предварительную выборку с 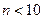 , по результатам измерения которого определяют S.
, по результатам измерения которого определяют S.
Пример: При обработке деталей 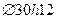 произошло смещение центра группирования размера. Рассчитать объем выборки, необходимый для определения среднего значения с точностью
произошло смещение центра группирования размера. Рассчитать объем выборки, необходимый для определения среднего значения с точностью 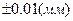 при
при 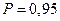 .
.
Допуск 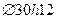 - 0.21 (мм). Ориентировочное значение
- 0.21 (мм). Ориентировочное значение 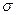 :
: 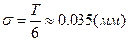 .
.
Рассчитываем объем выборки: 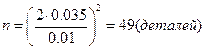 .
.
Часто встречающиеся законы распределения
| закон распределения | эскиз | Плотность вероятности 
| характеристика |
| Равной вероятности | 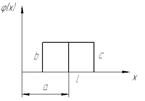
| 
| 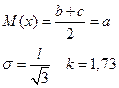
|
| Симсона | 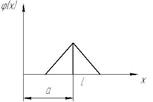
| 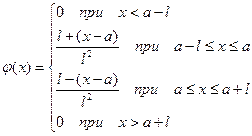
| 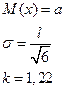
|
| Гаусса нормальный | 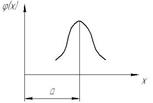
| 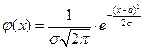
| 
|
| Релея | 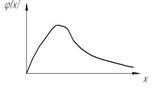
| 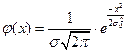
| 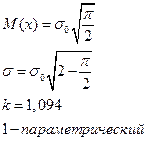
|
| Модуля разности | 
| 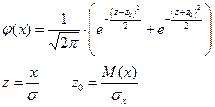
| 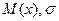 k зависит от соотношения
k зависит от соотношения 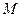 и и 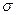
|
k – коэффициент относительного рассеивания
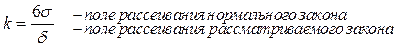
Закон равной вероятности встречается при ошибках округления по шкале, ошибках от воздействия фактора, изменяющегося по линейному закону, например, износа инструмента.
Закон Симпсона встречается при сложении двух случайных величин, распределенных по закону равной вероятности, например, отсчёт по шкале не от нуля.
Закон Гаусса(нормальный закон)
По центральной предельной теореме Ляпунова: если случайная величина состоит из суммы случайных величин и не одна из них не доминирует, то суммарная величина распределена по нормальному закону.
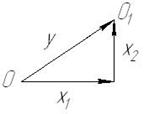
Закон Релея (закон экцентриситета): если величины 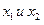 аспределены по нормальному закону, то величина
аспределены по нормальному закону, то величина 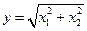 распределена по закону Релея.
распределена по закону Релея.
Модуль разности: если величины 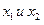 распределены по нормальному закону, то величина
распределены по нормальному закону, то величина 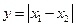 распределена по закону модуля разности. По этому закону распределены погрешности формы и расположения: - отклонения от параллельности
распределена по закону модуля разности. По этому закону распределены погрешности формы и расположения: - отклонения от параллельности  , отклонение от перпендикулярности
, отклонение от перпендикулярности  , конусность, овальность и т.д.
, конусность, овальность и т.д.
|
|
|


