 |
Интегральные функции. Функция Лапласа. Определение процента брака.
|
|
|
|
Для определения процента годных и негодных изделий необходимо определить вероятность попадания значения в заданный интервал.
Вероятность того, что случайная величина меньше x равна заштрихованной площади под кривой (Рис.3).
Рис. 3 Определение годной и негодной продукции.
Площадь под кривой равна интегралу от плотности вероятности или интегральной функции.
Интегральная функция или функция распределения F(x) равна вероятности того, что в результате опыта случайная величина приняла значение меньше x.
F(x)=P(ξ<x)
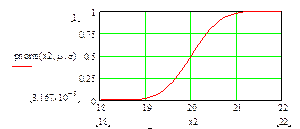
Рис.4 Функция распределения или интегральная функция.
Для вычисления интеграла часто пользуются функцией Лапласа. Для этого делается замена переменной x на t по нижеприведенным формулам, а функция Лапласа Ф(t) табулируется.
Замечание: функция распределения F(x) имеет пределы интегрирование от минус бесконечности до x, а функция Лапласа Ф(t) – от 0 до t.
Для определения процента брака в Mathcad используют интегральную функцию pnorm. 
где μ – математическое ожидание, σ – среднеквадратичное отклонение, x – предельное значение случайной величины.
Например, найти процент бракованных заготовок диаметром 20-1.
Для определения процента брака необходимо найти максимальный предельный диаметр dmax, минимальный предельный диаметр dmin, среднее значение μ и среднеквадратическое отклонение σ.
dmax=d+es, dmin=d+ei где d – номинальный диаметр, es – верхнее предельное отклонение, ei – нижнее предельное отклонение.
dmax=20+0=20, dmin=20+(-1)=19
Среднее значение элементов массива 
Среднеквадратичное отклонение 
Процент изделий с размером менее 19 равен 2,3%, а более 20 – 9,1%
Зависимость между величинами.
|
|
|
Уравнение регрессии.
Коэффициент корреляции и корреляционное отношение.
Две величины могут быть независимы или связаны функциональной, вероятностной или корреляционной зависимостью.
Величины называются независимыми, если значение одной величины не зависит от значения другой.
При функциональной зависимости, каждому значению одной величины отвечает вполне определенное значение другой (одно или несколько)
При вероятностной (стохастической, статической) зависимости, каждому значению одной величины отвечает множество значений другой величины, причем каждое из значений «y» имеет вполне определенную вероятность.
Вероятностная зависимость называется корреляционной, если с изменением одной величины изменяется только среднее значение другой, а дисперсия и закон распределения не меняются.
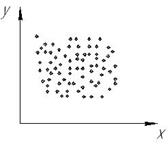
Независимые величины Функциональная Вероятностная
зависимость
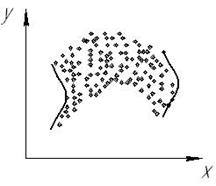
корреляционная
Распределение плотности вероятности, соответствующей фиксированному значению одного из параметров, называется условным распределением, а соответствующие этому распределению средние значения и дисперсия соответственно условными средними и условными дисперсиями.
Линии, соединяющие условные средние, называются линиями регрессии или теоретическими кривыми регрессии (regression-движение назад, возвращение).
Уравнение, выражающее изменение условного среднего значения одного параметра в зависимости от значения другого, называется уравнением регрессии или уравнением корреляционной связи.
(регрессия y на x)
При методе наименьших квадратов коэффициенты уравнения регрессии 
рассчитывается так, чтобы сумма квадратов отклонении экспериментальных значение от расчетных была наименьшей.
Если - степенная зависимость 
, то коэффициенты уравнении регрессии могут быть найдены:
|
|
|
