 |
Оптимальное соотношение ресурсов
|
|
|
|
До сих пор мы считали переменным только один фактор производства (ресурс) — труд. Но известно, что в долговременном периоде фирма способна изменять количества всех ресурсов, применяемых ею в производстве.
Возникают вопросы:
1. Каким должно быть сочетание ресурсов для производства любого данного объёма производства с наименьшими издержками? (min АТС).
2. При каком сочетании ресурсов прибыль максимальна (max П)?
Начнём с ответа на первый вопрос.
труд
Допустим: используются только 2 ресурса:
и капитал
Правило минимизации издержек:
Минимальными издержки будут тогда, когда в производстве любого
Q (объёма продукции), дополнительный рубль, вложенный в ресурс, принесёт одинаковый предельный продукт:
Условие минимизации издержек АТС→min
(1)
Мы уже встречались в теории потребительского поведения с очень похожим равенством. Но там речь шла о максимизации полезности потребителем: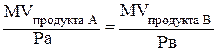 
. Она наступала в результате перераспределения расходов потребителя в пользу товара с большей полезностью на 1 рубль его цены, т.к. это приводило к большей общей полезности. Процесс перераспределения заканчивался, когда равенство выполнялось.
Минимум издержек для производителя — это то же, что максимум полезности для потребителя → вот почему похожи эти равенства.
Рассмотрим пример.
Пусть при одной и той же цене труда и капитала (=1) производитель получает МРкапитала =5, а предельный продукт труда = 8; равенство не выполняется 8/1 ≠ 5/1. Если фирма затратит на капитал на 1 рубль меньше, она потеряет 5 единиц продукции. А, вложив этот рубль в труд, получит
8 единиц продукции. Т.е. при тех же общих затратах объём продукции вырастет на 8 – 5 = 3 единицы. Значит, средние общие издержки снижаются (АТС=ТС/Q↑). Когда перелив рублей капиталом и трудом достигает точки, где выполняется равенство (1), то уже нельзя будет увеличивать объём и тем самым снижать издержки. Издержки достигли минимальной величины.
|
|
|
Второй вопрос: при каких сочетаниях ресурсов прибыль максимальна → так же важен для фирмы.
Существует много разных уровней объёма производства (Q), при которых фирма может производить продукт с наименьшими затратами:
Но есть один-единственный уровень объёма производства, при котором прибыль максимальна.
Из анализа 4-ёх моделей рынка известно, что условие максимизации прибыли: MR = MC. Как это равенство будет выглядеть с точки зрения затрат на ресурсы?
Из примера (табл.1) мы выяснили: максимизирующая прибыль фирма будет нанимать работников до точки, в которой ставка з/п (цена труда, РL) равна предельной доходности труда (или предельному продукту в денежном выражении) MRP, т.е. W = PL = MRPL. Отсюда MRPL/ PL = 1.
Точно так же, как труд в качестве переменного ресурса может быть рассмотрен капитал. Повторив расчёт, как в примере 1, применительно к капиталу получим, что максимизирующая прибыль фирма будет использовать такое количество капитала, при котором его цена (РК) равна его предельному продукту в денежном выражении MRPK, т.е. РК= MRPK.
Можно записать это равенство иначе: MRPK/ РК=1, т.е. для максимизации прибыли фирма использует такие количества труда и капитала, чтобы выполнялось равенство (2): 
(2)
Если числитель в равенстве (2) поделить на цену продукта, то получим равенство (1).
(MRP = ∆TR/∆L = ∆ (P*Q)/ ∆L; p = const; MRP/P = ∆Q/∆L = MP). Т.е. необходимым условием для максимизации прибыли является соблюдение равенства (1), т.е. минимизация издержек.
Но обратное утверждение, что равенство (1) есть достаточное условие для максимизации прибыли → неверно (фирма может достичь минимальных издержек, но её объём Q не обеспечивает при этом максимума прибыли).
|
|
|
Рассмотрим пример: фирма использует труд (по цене 8 д.е.) и капитал (по цене 12 д.е.). Примем, что производительность каждого ресурса не зависит от количества другого ресурса. Цена продукта р = 2 д.е.
| Труд (цена =8д.е.) | Капитал (цена = 12 д.е.) | ||||||||
| Кол-во ресурса (труда), L | QL | MPL | TR=P*Q (P=2) | MRPL=∆TR/∆L | Кол-во ресурса (капитала) K | QK | MPK | TR=P*Q (P=2 д.е.) | MPRK |
| - | - | - | - | - | |||||
| 12*2=24 | |||||||||
1.Выясним: каково соотношение труда и капитала, обеспечивающее наименьшие издержки при производстве, например, Q = 50 ед. продукции.
Ответ: 3 единицы труда и 2 единицы капитала.
Почему? Необходимо выполнение равенства (1):
Проверим.
а). При L = 3, MPL = 6 и PL = 8. 
При К = 2 MPK = 9 и PK=12. 
.
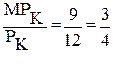В результате такого соотношения труда и капитала производится
Q = 28 + 22 = 50 изд. А чему равны издержки?
Издержки ТС = 3 · 8 + 2 · 12 = 48 д.е. Средние общие издержки
АТС = 48/50 = 0,96.
Проверим, является ли величина издержек действительно минимальной?
Объём Q = 50 может быть достигнут и другим сочетанием труда и капитала: при L = 5 и К = 1. При этом Q = 37 + 13 = 50. А издержки
ТС= 5 · 8 + 1 · 12 = 52; АТС = 52/50 =1,04.
б). Издержки не минимальны, т.к. равенство (1)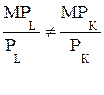 
,
не выполняется: при L = 5, МР = 4;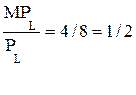 
,
при K = 1 MP = 13; 
, → значит фирме надо применять меньше труда и больше капитала.
в). Наконец, объём Q = 50 может быть достигнут и другим сочетанием труда и капитала при L = 2 и К = 3. При этом Q = 22 + 28 = 50. А издержки
ТС = 2 · 8 + 3 · 12 = 52; АТС = 52/50 = 1,04.
; 
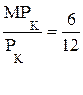. Равенства нет. Фирме надо увеличивать количество применяемого труда и уменьшать количество капитала.
Итак, объём Q=50 может быть достигнут различными сочетаниями L и К, но только соотношения, отвечающее равенству (1), → минимизирует издержки.
1.Принесёт ли объём Q = 50 максимальную прибыль фирме?
Для ответа нужно выяснить, соблюдается ли равенство (2)?
При L = 3 и К = 2 прибытьне является максимальной, т.к. 
,
а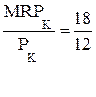 
.
Просмотрев столбец MRPL, найдём в нём строку, где 
|
|
|
это L = 5. Из столбца MRPK увидим, что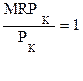 
при К = 3.
Итак, равенство (2) выполняется при L = 5 и К = 3. Именно это соотношение ресурсов обеспечивает максимум прибыли.
П = TR – TC = (p · Q∑ – (PL ·L + PK · K)) =
= ((37 + 28) · 2) – (5 · 8 + 3 · 12)) = 130 – 76 = 54 д.е.
Проверим: а удовлетворяется ли равенство (1)?
При L = 5 MPL = 4 K = 3 MPK = 6
PL = 8 PK = 12,
(1)
4/8 = 6/12 выполняется, т.е. издержки минимальны для Q = 65 именно при К=3 и L=5.
Итак, общий подход к решению такого типа задач:
а). если требуется найти [L, К], при котором АТС = min, то нужно рассчитать столбцы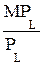 
и 
.
Соотношения, при котором численные значения
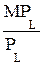и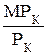 
совпадают → и есть искомое сочетание ресурсов, минимизирующее издержки [L, К].
б). если же требуется найти такое соотношение [L, К], при котором
П = max, то рассчитывают столбцы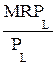 
и 
и находят те значения L и К, при которых эти соотношения равны единице, т.е.
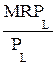= =1. Само собой, что при выполнении равенства (2), выполняется и равенство (1).
Контрольные вопросы.
1.Что отличает кривые спроса на труд (dL) в условиях совершенной и несовершенной конкуренции?
|
|
|
