 |
Парамагнитная и диамагнитная восприимчивость электронов проводимости
|
|
|
|
Парамагнетизм Паули.
До сих пор вклад электронов проводимости в магнитные свойства не учитывался. При рассмотрении влияния электронов используется приближение свободных электронов, учитывается только спиновый угловой момент и не учитывается заряд электрона. Каждый электрон вносит вклад в намагниченность, равный -mB/V, считая g0 = 2, если S H и +mB/V, если S ¯ H, тогда намагниченность
 |
M=mB(n+ - n-) (3.20)
Пусть g±(E)dE –плотность состояний, т.е. отнесенное к единице V число электронов с определенным значением спина («+» соответствует параллельной (), «-» - антипараллельной (¯) ориентации спинов) и с энергией в интервале Е ¸ Е+dE.
В отсутствие поля (H=0): g±(E)=1/2g(E), (3.21)
Если же H¹0, то
DE = -gmBH при S H и DE = +gmBH при S ¯ H, (3.22)
электроны с и ¯ направлениями спина перераспределяются так, что на поверхности Ферми их энергии равны (рис.3.3), а плотности состояний g+(E) и g-(E) различны:
g+(E)=1/2g(E+mB H); (3.23а)
g-(E)=1/2g(E-mB H). (3.23б)
Число электронов в единице объема
n±=òdEg±(E)f(E), (3.24)
где f=1/(eb(E - m)+1) – распределение Ферми-Дирака.
Воспользуемся равенством n=n++n- и (3.23), чтобы исключить химический потенциал m. В невырожденном случае (Е-m >> kBT, f»exp [-b(E-m)]) мы приходим к полученным ранее выражениям для парамагнетизма диэлектриков с намагниченностью, совпадающей с (3.11) (закон Кюри - Бриллюэна M=N/V gμBJBJ(bgμBJH)) с J = 1/2, β = kBT.
Однако, чаще в металлах - сильное вырождение, т.е. Е-m << kBT. Плотность уровней g(E) существенным образом меняется только в масштабе EF, а поскольку mBН ~ 10-4 ЕF, даже в поле 104 Гс, то можно разложить по малому параметру mBН:
g±(E)=1/2g(E±mB H)=1/2g(E)±1/2mBHg'(E); (3.25)
n±=1/2òg(E)f(E)dE±1/2mBHòdEg'(E)f(E). (3.26)
При этом n=òg(E)f(E)dE, что совпадает с формулой для H=0, поэтому можно считать, что химпотенциал имеет такое же значение, что и при H=0:
|
|
|
m=EF[1+О((kBT/EF)2)]. (3.27)
В соответствии с (3.20), из (3.21) и (3.26) получаем:
M=mB2Hòg'(E)f(E)dE. (3.28)
Или, интегрируя по частям,
M=mB2Hòg(E)(-¶f/¶E)dE. (3.29)
При T=0: -¶f/¶E=d(E-EF) и тогда
M=mB2Hg(EF), c=mB2g(EF). (3.30)
Эти формулы описывают парамагнетизм Паули.
Поскольку температурные поправки к -¶f/¶E имеют порядок (kBT/EF)2 формулы (3.30) остаются справедливыми до очень высоких температур (T»104К). В парамагнетизме Паули М и c от температуры практически не зависят, в противоположность парамагнетизму ионов (c ~ 1/T).
В случае свободных электронов g(EF)=mkF/h2p2 и, соответственно,
cP=(a/2p)2(a0kF), a=e2/hc=1/137, cP=(2.59/(rs /a0)*10-6 ~ 10-6. (3.31)
cparPauli = cparion (T/TF). cPteor ~ 0.66 10-6, cPexp = 2.0 10-4.
Диамагнетизм Ландау.
Помимо парамагнетизма Паули электроны проводимости обладают диамагнетизмом, обусловленным взаимодействием спина электрона с внешним полем H. В сильных полях, при низких температурах и в чистых материалах наблюдаются осцилляции М(H) - эффект де Гааза-ван Альфена при условии wct=eBt/mc>>1. В обычных условиях это условие не выполняется и осцилляторная зависимость не наблюдается, но среднее значение М(H) не обращается в нуль и имеется результирующая намагниченность антипараллельная (¯) H. Это явление называется диамагнетизмом Ландау. Оно обусловлено орбитальным движением электронов в магнитном поле. Ландау показал, что для свободных электронов
cL=-1/3cP. (3.32)
В эксперименте разделить вклады диамагнетизма Ландау, ларморовский диамагнетизм, парамагнетизм Паули и ионный (Ланжевена) - сложная задача. Один из способов - ЯМР.
Учитывая диамагнетизм Ландау, парамагнетизм электронов проводимости в металлах составляет cpar= 2/3cP. Схематически температурная зависимость парамагнитных и диамагнитных свойств проиллюстрирована на рис.3.4.
IV. ФЕРРОМАГНЕТИЗМ
К ферромагнетикам относятся такие вещества, которые обладают так называемой спонтанной намагниченностью, т.е. М ¹ 0 при Н = 0. Среди них 9 моноатомных металлов
|
|
|
3d: Fe, Co, Ni
4f: Gd, Dy, Tb, Ho, Er, Tm
и бесчисленное количество сплавов и химических соединений (в том числе сплавов с неферромагнитными элементами – Гейслеровы сплавы – F.Heusler-1898г., см. Главу XIII). Характеристики некоторых из них приведены в Таб. 4.1
Таблица 4.1. Ферромагнитные вещества.
| Вещество | Намагниченность Ms (Гс) | n(0K)=μ/μB | TC, K | |
| Т = 300 К | Т= 0К | |||
| Fe | 2.22 | |||
| Co | 1.72 | |||
| Ni | 0.606 | |||
| Gd | - | 7.63 | ||
| Dy | - | 10.2 |
Спиновая природа ферромагнетизма установлена в опытах Эйнштейна - де Гааза и Барнетта (1915г.), схематично поясняемых на рис. 4.1. Оказалось, что для ферромагнетиков гиромагнитное отношение Mмаг/Mмех = mB/hs=(eh/2mc)/h1/2=e/mc, т.е. в 2 раза больше чем для парамагнетиков и диамагнетиков, магнетизм которых, как мы знаем из предыдущей главы, обусловлен орбитальным движением электронов. Парадокс разрешился введением в 1925г. Дж.Уленбеком (G. Ulenbeck) и С. Гаудсмитом (S. Goudsmit) понятия собственного механического момента электрона – спина, равного ½, предложившими эту идею на основе анализа спектроскопических данных.
Рис. 4.1. Схема опыта Эйнштейна-де Гааза.
|
Какова же природа упорядочения нескомпенсированных магнитных моментов отдельных атомов?
Внутреннее молекулярное поле Вейсса (P.Weiss )
Впервые идею о внутреннем молекулярном поле в ферромагнетике, вызывающем самопроизвольную намагниченность высказал Розинг (1892г.). Вейсс предложил аналогичную идею в 1907г.
Рис. 4.2. Температурная зависимость спонтанной намагниченности при Ва=0.
|
Согласно Вейссу внутреннее молекулярное поле, BW, аналогично внешнему полю Ва в парамагнетике, создает в кристалле ферромагнетика -ную ориентацию магнитных моментов при Ва = 0. В свою очередь, поле BW, называемое еще полем Вейсса, вызывается намагниченностью.
Закон Кюри-Вейсса.
В приближении среднего поля (mean field aproximation) BW µ M
B W=l M l=const(T); (4.1)
B эфф= B a+l M. (4.2)
В парамагнитной фазе M =cP(B a+ B W), где cP=С/T -закон Кюри.
Отсюда:
MT=С(Ba+lM) M=СBa/(T-Сl) и c=M/Ba=С/(T-Сl). (4.3)
При T=Тс=Сl - сингулярность (1/c à 0 на рис.4.2), которая соответствует спонтанной намагниченности. При Т £ Tc восприимчивость c®¥, намагниченность остается конечной М≠0 и в отсутствии поля, т.е. при Ва =0. Температурные зависимости обратной восприимчивости 1/χ для Т>Tc=Cl и спонтанной намагниченности М(Т)/Мs для Т<Tc приведены на рис.4.2.
|
|
|
Из (4.3) следует соотношение, называемое законом Кюри-Вейсса,
c=C/(T-TС);TC=Сλ. (4.4a)
Более точно:
c µ 1/(T-TС)1.33 при Т >» Тс. (4.4б)
Из определения константы Кюри C=N(J+1)Jg2mB2/3kB (для J=S):
l=TС/C=3kBTС/Ng2S(S+1)mB2. (4.5)
Для Fe (Тс»1000K, g»2, S=1) из (4.5) получаем l=5•103. При MS»1700Гс имеем BW»lM»(5*103)(1.7*103)~107Гс~103 Тл. Т.е. поле Вейсса гораздо сильнее магнитных полей (парамагнитных) ионов.
Рис. 4.4. Параллельная ориентация спинов в ферромагнетике
|
Электростатическая природа поля Вейсса.
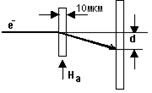Рис.4.3. Схема опыта Дорфмана.
|
Опыт Дорфмана (1927г.) доказал немагнитную природу внутреннего молекулярного поля в ферромагнетике. Если фольга (рис.4.3) намагничена до насыщения и поле Вейсса имеет магнитную природу, то отклонение электронного пучка d (силой Лоренца в магнитном поле) должно определяться эффективным полем Ba+Bw, существенно более сильным, чем Ba (Bw~103Тл!). В эксперименте Дорфмана же отклонение соответствовало эффективному полю Ba~ 1 Тл, что свидетельствовало в пользу электростатической природы поля Вейсса.
В 1928г. Френкель и Гейзенберг предположили, что ферромагнетизм есть особое свойство электростатически взаимодействующих электронов. В результате электростатического взаимодействия между электронами выгодным оказывается состояние с -ной ориентацией спинов соседних атомов (ионов) (рис.4.4).
Модель Гейзенберга .
Наряду с классическим кулоновским взаимодействием, гамильтониан содержит чисто квантовый член, зависящий от ориентации спинов. Этот вклад обусловлен обменным взаимодействием, описываемым гамильтониан Гейзенберга
DHобм= -J (S 1 S 2), (4.6)
где J- обменный интеграл.
Рис. 4.5. Пояснение к обозначениям в тексте.
|
Если J>0, то DEобм= -2J(S 1 S 2), для S1,2=1/2 S 1 S 2= 1/4
Рис. 4.6. Качественный вид зависимости J(R/a).
|
J<0 S 1 S 2= -1/4.
Для большого числа электронов обменная энергия равна
DEобм = -åijJij(S i S j). (4.7)
|
|
|
Для 2-х электронов - 4 состояния (3 триплетных и 1 синглетное)
J =1/2(ES-Et). (4.8)
J>0®Et<ES, J<0 ® Et>ES.
Для системы из 2-х атомов водорода интеграл перекрытия имеет вид
J=e2ò(1/r-1/ra2 - 1/rв1) ·Y*a(1)Y*в(2)Ya(1)Yв(2)dr1dr2. (4.9)
Обозначения поясняются на рис. (4.5).
На рисунке 4.6 качественно изображена зависимость J(R/a), где R - расстояние между атомами, а-радиус недостроенной оболочки (d или f)
Рис. 4.7. Иллюстрация видов обмена.
|
Механизмы обмена спинами.
Прямой обмен - непосредственный обмен между магнитными ионами (модель Гейзенберга) (рис.4.7).
Сверхобмен - обмен через немагнитного атома-посредника.
Косвенный обмен (С.П.Шубин, С.В. Вонсовский) - обмен через электроны проводимости. Характерен для РЗ-металлов.
Спиновые волны. Магноны.
Строго параллельная ориентация соответствует минимуму энергии и температуре 0К. С повышением температуры растет число "перевернутых" спинов. Состояния с антипараллельными спинами являются "возбужденными". Переворот одного спина требует энергии
DE=-J(S(-S)+(-S)S) - (-J[SS+SS])» 4JS2 . (4.10)
Рис.4.8. Спиновые волны
|
Т.е. состояния с перевернутыми спинами являются невыгодными энергетически. Соседние спины стремятся перевернуть (возвратить) спин в исходное положение. Обменное взаимодействие приводит к тому, что при этом соседний спин сам переворачивается. По кристаллу пробегает волна перевернутых спинов (рис.4.8). Волны называются спиновыми волнами (Ф. Блох,1930).
Магноны - это кванты энергии спиновых волн. При малой плотности магноны ведут себя как идеальный газ, подчиняющийся статистике Бозе-Эйнштейна.
n(k)=<nK>=1/(exp(E(k)/kBT)-1); (4.11а)
M(T)=M(0)[1-(1/NS) åkn(k)], (4.11б)
где M(0)=gmB(N/V)S - намагниченность насыщения.
Число магнонов растет µ nmag µ Т3/2, соответственно, М µ 1/ Т3/2. При Т < Tc выполняется закон Блоха
M(T)=M(0)[1-b(T/Tc)3/2], b» 1, (4.12)
качественно изображенный на рис.4.2 при Т < Tc.
|
|
|
