 |
Измерительные информационные 4 глава
|
|
|
|
рассмотрим эти погрешности как случайные величины. Природа
«случайности» у них различна.
Случайные погрешности в результатах измерений являются следствием многочисленных причин, например из-за физических процессов, происходящих в работающем приборе (трения, слу- чайного дрейфа характеристик элементов, шумов), или случай- ных изменений условий измерения, учет которых практически неосуществим. «Случайность» оценок систематических погреш- ностей – результат незнания или технической невозможности (например, ограниченной точности средств аттестации методик измерения) идеального определения их истинных значений. Од- нако влияние случайных погрешностей на конечный результат измерений можно уменьшить увеличением числа измерений. Приведенные ниже вероятностно-статистические модели случай- ных величин справедливы как для случайных и неисключенных систематических составляющих, так и для суммарной погрешно- сти измерений.
Теория погрешностей, использующая математический аппарат теории вероятностей, основывается на аналогии между появлени- ем случайных результатов при многократно повторенных изме- рениях и случайных событий.
Из теории вероятности известно, что для описания случайных величин используют законы ее распределения.
Закон распределения случайной величины устанавливает со- отношение между возможными значениями случайной величины X и соответствующими им вероятностями. Закон распределения может быть задан в виде таблиц, формул, графически. Он дает полную информацию о свойствах случайной величины, позволя- ет оценить ее значение и определить вероятность нахождения ее значения в заданных границах.
|
|
|
Для дискретных и непрерывных (рис. 1.2, а) случайных вели- чин на практике часто применяют закон распределения в виде интегральной функции распределения F(x). Эта функция опреде- ляется вероятностью того, что случайная величина Xi в i опыте примет значение, меньшее некоторого значения х:
F(x) = P(Xi < x) = P( -¥ < Xi < x).
Интегральная функция распределения имеет следующие свой- ства: она неотрицательная, т.е. F(x) > 0; неубывающая, т.е. F(X2)
> > F(X2), если X2> X1; изменяется от 0 до 1, т. е.
F(- ∞)=0,F(+∞) = 1.
Важным свойством, объясняющим универсальность и практи- ческую применяемость функции распределения, является то, что вероятность нахождения случайной величины Х в интервале (включая нижнюю границу) от x 1 до x 2 равна разности функций распределения, т.е.:
P (X 1< X < X 2) = F (X 2) - F (X 1).
(1.9)
Для описания распределения непрерывных случайных вели- чин часто пользуются первой производной функции распределе- ния F'(х), которую называют плотностью распределения. Это связано с тем, что производную функции распределения
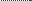p (x) = F ¢(x) = dF (x)
dx
статистически (экспериментально) значительно
проще определить, чем саму функцию распределения.
Плотность вероятности р(х) (дифференциальная функция рас- пределения) определяется как предел отношения вероятности того, что случайная величина X примет значение внутри беско- нечно малого промежутка от х до х + dx к величине этого проме- жутка dx, когда dx →0:
p (x) = lim
dx ®0
P ( x £ X < x + dx ) dx
(1.10)
Функция распределения выражается через плотность вероят- ности:
x
F (x) = P (X < x) = ò P (X) dx.
-¥
F(X)
1
P(X)
0 X 0
х1 х2 X
а б
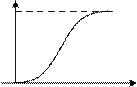
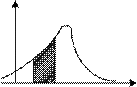
Рис. 1.2. Законы распределения непрерывной случайной величины: а – интегральный; б – дифференциальный
Вероятность попадания случайной величины в заданный ин- тервал (X1,X2) определяется как:
x 2
P (x 1< X < x 2) = F (x 2) - F (x 1) = ò P (X) dx.
x 1
Графически эта вероятность равна площади криволинейной трапеции, ограниченной кривой распределения, осью абсцисс и прямыми Х=x1, и Х= x2 (рис. 1.2, б).
|
|
|
Статистическое описание случайной величины законами рас-
пределения достаточно сложно. На практике ограничиваются числовыми характеристиками законов распределения случайной величины, которые характеризуют определенные свойства этих законов распределения. Среди числовых характеристик случай- ных величин математическое ожидание, мода и медиана являют- ся характеристиками положения случайной величины на число- вой оси.
Математическое ожидание случайной величины (ее сред- нее значение) определяется как сумма произведений всех воз- можных значений дискретной случайной величины Х на вероят- ность этих значений Р:
i = n
M [ X ]= å X i Pi.
i =1
(1.11)
Для непрерывной случайной величины математическое ожи- дание:
-¥
M [ X ]= ò XP (P) dx,
+¥
(1.12)
где Р(Х) – плотность распределения вероятностей случайной ве- личины X.
Мода M0[X] – значение случайной величины X, имеющее у дискретной величины наибольшую вероятность, а у непрерывной
– наибольшую плотность вероятности. Кривую распределения, имеющую один максимум, называют одномодальной (см. рис. 1.2, б), два максимума – двухмодальной, несколько одинаковых максимумов – многомодальной.
Медиана Mв[Х] случайной величины X характеризует такое ее значение, для которого одинаково вероятно, окажется ли случай- ная величина меньше или больше Mв[Х]. В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.
Характеристиками рассеивания случайной величины являются дисперсия и среднеквадратичное отклонение.
Дисперсия случайной величины X – математическое ожида- ние квадрата отклонения случайной величины от ее математиче- ского ожидания. Для дискретной случайной величины дисперсия
n
|
(1.13)
i =1
для непрерывной случайной величины:
+¥
D [ X ] = M [{ X - M (X)}2 ] =
ò{ X i
- M (X)}2 P (X) dX.
(1.14)
-¥
Среднеквадратичное отклонение случайной величины квад- ратный корень из дисперсии:
d [ X ] =
D (X).
Кроме рассмотренных характеристик положения и рассеива- ния случайных величин используют ряд вероятностных характе- ристик, каждая из которых описывает то или иное свойство рас- пределения. К таким характеристикам относятся начальные и центральные моменты. Математическое ожидание случайной ве- личины X есть ее первый начальный момент М [ Х ] = α 1, а диспер- сия – второй центральный момент D [ X ] =µ 2. Третий центральный момент µ 3характеризует степень асимметрии (скошенности) кривой распределения относительно математического ожидания. Для удобства за характеристику асимметрии принимают безраз- мерную величину, называемую коэффициентом асимметрии
|
|
|
A = M [(X - M (X)) ].
S (d (X))3
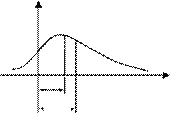
При одномодальном распределении асимметрия положитель- на (AS > 0), если мода M0 [ X ] находится слева от среднего значения М [ Х ], и отрицательна (AS < 0), если мода M0 [ X ] находится справа от среднего значения М [ Х ] (рис. 1.3). При симметричном распре- делении AS = 0 (рис. 1.4, а).
Четвертый центральный момент jх4 численно характеризует островершинность или плосковершинность кривой распределе- ния и определяется безразмерной величиной Ex, называемой экс- цессом:
|
P(X)
P(X)
AS>0
AS<0
0 M0 X
M(X)
а
0 M(X) X
M0
б
Рис. 1.3. Кривые плотности вероятности с положительными (а) и отрицательными (б) коэффициентами асимметрии
P(X) Ex>0
Ex=0
Ex<0
а б
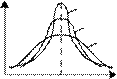
Рис. 1.4. Кривые плотности вероятности с различными коэффициентами эксцесса
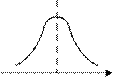
При симметричном одномодальном распределении эксцесс положителен (Ex > 0), если кривая распределения островершинна, и отрицателен (Ех < 0), если кривая плосковершинна. Эксцесс равен нулю (Ex = 0) при нормальном распределении (рис. 1.4, б).
Используя эти три момента, можно построить теоретическую модель закона распределения.
Одним из наиболее часто употребляемых в метрологической практике теоретических законов распределения погрешностей измерения является нормальный закон распределения, обладаю- щий свойствами симметрии и монотонного убывания плотности вероятности:
· равные по абсолютному значению, но противоположные по знаку погрешности встречаются одинаково часто (аксиома сим- метрии);
|
|
|
· малые погрешности встречаются чаще, чем большие; очень большие погрешности не встречаются.
Нормальное распределение центрированной случайной вели- чины (погрешности) при М(Δ) = 0 является одномодальным и описывается выражением
P (D) =
d
1 e -D / 2 s.
|
(1.16)
Для нормального закона распределения вероятность нахожде- ния погрешности между значениями X1 и X2 определяется разно- стью соответствующих значений функции распределения:
x 2
1 2 2
P (X 1
< D > X
2) = F (X
2) - F (X 1) =
d
ò e -(D) / 2 s dx.
2 p x 1
(1.17)
Графически эта вероятность представлена площадью под кри- вой, изображающей плотность вероятности между ординатами, соответствующими абсциссам X1 и X2.
Графики плотности (1.16) нормального распределения по- грешности при различных значениях δ приведены на рис. 1.5.
Очевидно что, чем меньше δ, тем круче кривая падает к оси Δ
и тем она островершиннее (δ 1< δ 2< δ 3).
Нормальный закон реализуется в тех случаях, когда погреш- ность измерений обусловливается большим числом случайных факторов (более четырех), каждый из которых вносит свою при- близительно одинаковую с другими долю в общую погрешность. При этом законы распределения составляющих погрешностей могут быть самыми различными (равномерными, треугольными, трапецеидальными, экспоненциальными и др.).
Если x1= -∞, а x2= +∞, то вероятность, определенная по (1.17), обратится в единицу, что соответствует площади под кривой (см. рис. 1.2).
На практике для выполнения расчетов применяют нормиро- ванную функцию Лапласа, называемую также интегралом веро- ятностей
1 t 2 t
F(t) =
ò e - t / 2 dt = ò j (t) dt,
где t=x/δ.
2 p 0 0
Тогда расчетную вероятность нахождения погрешности в за- данных границах (X1, X2) можно найти, используя табличные зна- чения аргумента функции Лапласа:
P (x 1< D < x 2) = F(t 2) - F(t 1),
(1.19)
где t
x 1; x 2
1 = d
t 2= d.
Формула (1.19) позволяет рассчитать границы интервала (до- верительного интервала), в котором с определенной (до- верительной) вероятностью находится результат измерения (рис. 1.6).
ζ1
ζ2
ζ3
-4 -3 -2 -1
0 1 2 3 4 Δ
Рис. 1.5. Графики плотности нормального распределения погрешности при различных значениях δ
Основными точечными характеристиками погрешности изме- рений, которые оцениваются расчетным путем (до проведения измерений) по характеристикам используемых методов и средств
измерений или по результатам измерений (после осуществления измерительного процесса), являются математическое ожидание, дисперсия и среднеквадратичное отклонение.
1
0,5
P(X) 0,4
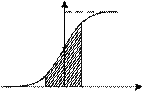
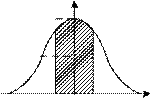0,2
а) б)
Рис. 1.6. Нормированные функции распределения: а – интегральная;
|
|
|
б – дифференциальная
Оценкой математического ожидания (МО) случайной величи- ны является среднее арифметическое значение (СКО) измеряемой величины:
n
|
n i =1
(1.20)
Точечная оценка дисперсии:
i = n
D [ X ] =
1 å(X
- X) 2.
(1.21)
|
Для получения характеристики рассеивания результатов во- круг среднего арифметического значения в абсолютных единицах используют среднеквадратичное отклонение
i = n
s [ X ] =
D (X) =
1 å(X
- X) 2.
(1.22)
|
Полученные оценки – математическое ожидание и средне- квадратичное отклонение являются случайными величинами, по- этому СКО X используют для оценки разброса X:
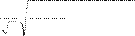
S
S = X
i = n
- X) 2,
(1.23)
X n n (n -1) i =1
а СКО δ[Х] – для оценки разброса δ[Х]:
Ex -1
Sd = SX
2 n
, (1.24)
где EX – численное значение эксцесса.
Точечные оценки, характеризующие параметры распределе- ния в виде чисел, обычно используют при большом объеме вы- борки. С уменьшением объема выборки степень их достоверно- сти уменьшается, поэтому переходят к интервальным оценкам, позволяющим определить интервал (доверительный), в котором с заданной вероятностью (доверительной) находится истинное зна- чение оцениваемого параметра.
Вероятность того, что действительное значение измеряемой ве- личины X находится внутри доверительного интервала (X - x 2, X + x 1), называется надежностью β при заданной точности.
В практике измерений применяют различные значения дове-
рительной вероятности, например: 0,90; 0,95; 0,98; 0,99; 0,9973 и 0,999. Доверительный интервал и доверительную вероятность выбирают в зависимости от конкретных условий измерений. Так, например, при нормальном законе распределения случайных по- грешностей со среднеквадратичным отклонением δ часто поль- зуются доверительным интервалом от +3 δ до -3 δ, для которого доверительная вероятность (по статистическим таблицам значе- ний функции Лапласа) равна 0,9973. Такая доверительная веро- ятность означает, что в среднем из 370 случайных погрешностей только одна погрешность по абсолютному значению будет боль- ше 3 δ. Так как на практике число отдельных измерений редко превышает несколько десятков, появление даже одной случайной погрешности, большей 3 δ, маловероятное событие, наличие же двух подобных погрешностей почти невозможно. Это позволяет с достаточным основанием утверждать, что все возможные слу-
чайные погрешности измерения, распределенные по нормально- му закону, практически не превышают по абсолютному значению 3 δ (правило «трех сигм»). В случае, если погрешность выходит за значение Зст, то его можно считать «промахом». Для определения
«промаха» используют критерии «трех сигм» – Смирнова, Райта,
Романовского, Шовенэ и др.
1.10. Обработка результатов измерений
Прямые многократные измерения. Точно оценить действи- тельное значение измеряемой величины можно лишь путем ее многократных измерений и соответствующей обработки их ре- зультатов. Правильно обработать полученные результаты наблю- дений – значит получить наиболее точную оценку действитель- ного значения измеряемой величины и доверительного интерва- ла, в котором находится ее истинное значение. Обработка должна производиться в соответствии с ГОСТ 8.207–76 «ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Общие положения». В процессе обра- ботки результатов наблюдений необходимо последовательно ре- шить следующие основные задачи:
· определить точечные и интегральные оценки закона распре- деления результатов измерений [по формулам (1.20) и (1.22)];
· исключить «промахи» (по одному из критериев);
· устранить систематические погрешности измерений (см. разд. 1.8);
· оценить закон распределения по статистическим критериям (используются критерии x2 – Пирсона, Колмогорова, составной);
· определить доверительные границы неисключенного остатка
систематической составляющей [см. (1.26)], случайной составля-
ющей [см. (1.19)] и общей погрешности результата измерения (см. разд. 1.11);
· записать результат измерения (см. разд. 1.13).
Прямые однократные измерения. Погрешность результата прямого однократного измерения зависит от многих факторов, но в первую очередь определяется, естественно, погрешностью ис- пользуемых СИ. Поэтому в первом приближении погрешность результата измерения можно принять равной погрешности, кото- рой в данной точке диапазона измерений характеризуется ис- пользуемое СИ.
В общем случае задача оценки погрешности полученного ре- зультата обычно осуществляется на основе сведений о пределе допускаемой основной погрешности средства измерения Δ си (по нормативно-технической документации на используемые сред- ства измерений) и известным значениям дополнительных по- грешностей Δ доп от воздействия влияющих величин. Условно счи- тают, что методические и субъективные погрешности при прове- дении измерения незначимы. Тогда максимальное значение сум- марной погрешности результата измерения (без учета знака) можно найти суммированием составляющих по абсолютной ве- личине:
Då= | D си
m
| +å | D
i =1
доп
|. (1.25)
Более реальную оценку погрешности можно получить стати- стическим сложением составляющих погрешности:
Då= k
m
|
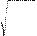
i =1
(1.26)
где Δi; – граница i -й неисключенной составляющей системати- ческой погрешности, включающая в себя погрешности средства, метода, дополнительные погрешности и др.; к – коэффициент, определяемый принятой доверительной вероятностью (при
Р = 0,95, коэффициент k = 1,11); m – число неисключенных состав- ляющих.
Результат измерения записывается по первой форме записи результатов согласно ГОСТ 8.011–72 «Показатели точности изме- рений и формы представления результатов измерений»:
xi;D = ±Då; P = 0,95,
где xi – результат однократного измерения; ΔΣ – суммарная по- грешность результата измерений; Р – доверительная вероятность (при Р = 0,95 может не указываться).
При проведении измерений в нормальных условиях можно считать Δ Σ = Δ си.
Методика обработки результатов прямых однократных изме- рений приведена в рекомендациях МИ 1552–86 «ГСИ. Измерения прямые однократные. Оценивание погрешностей результатов из- мерений».
Неравноточные измерения. В практике измерений имеют место также и неравноточные измерения, когда измерения одной и той же физической величины проводятся несколькими наблю- дателями различной квалификации и опыта, на приборах разного класса точности или в течение нескольких дней. Полученные значения средних арифметических отдельных выборок отлича- ются друг от друга, поэтому при оценке результата измерения и его погрешности учитывается степень доверия к полученным вы- борочным средним в виде «веса», который устанавливается для каждой серии измерений пропорционально одному из параметров (вероятности, числу измерений, величине среднеквадратичного отклонения) либо методом экспертных оценок. Если установлено, что все выборки неравноточных измерений принадлежат одной генеральной совокупности, то определяют статистические пара- метры этой генеральной совокупности и устанавливают границы доверительной вероятности по распределению Стьюдента.
В практике измерений случается, что при нескольких сериях измерений некоторые из них оказываются менее надежными. В этом случае степень доверия оценивается весом данной серии измерений. Чем больше степень доверия к результату, тем боль- ше число, выражающее вес. Среднее взвешенное значение изме- ряемой величины, наиболее близкое к истинному значению, со- ставляет
X P *+ X
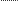
P *+...+ X P *
X = 1 1 2 2 m m, 0 P *+ P *+ P *+...+ P *
(1.27)
1 2 3 m
где
X 1, X 2 ,..., Xm
– средние значения для отдельных групп измере-
ний; P*,P*,...,P* – их вес.
1 2 m
В основу вычисления обычно кладут среднеквадратичные по- грешности. Веса соответственных групп измерений считают об- ратно пропорциональными их дисперсиям, т. е. используют зави- симость:
P *: P *: P *: P * =
1: 1: 1
: 1.
1 2 3
m 2 2 2 2
1 2 3 m
|
|
|
|
S 0 =
1,
|
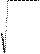
(1.28)
|
i
i =1
|
|
– вес каждого результата измерений; m – число рядов из-
мерений.
Косвенные измерения. При косвенных измерениях значение физической величины z определяется по функциональной зави- симости ее с другими физическими величинами a1,a2,…,am:
z=f (a1,a2,…,am). (1.29)
При этом погрешность оценки систематической Δc и случай- ной Δ величины z зависит не только от погрешностей результатов измерений a1,a2,…,am, но и от вида используемой функциональ- ной зависимости (1.29).
|
|
|
