 |
Измерительные информационные 5 глава
|
|
|
|
Пусть каждая из величин aj(j=1,2,…,m) измерена с системати- ческой погрешностью Δcj. Необходимо оценить значение погреш- ности Δz результата косвенного измерения.
Рассматривая z как функцию m переменных aj, запишем ее полный дифференциал:
dz = (df / da 1) da 1+ (df / da 2) da 2+...+ (df / dam) dam
или
m
dz = å(df / da j) da j.
i =1
Положив, что погрешности измерений достаточно малы, за- меним дифференциалы соответствующими приращениями:
m
D cz = å (df / da j) D caj. (1.30)
j =1
Каждое слагаемое вида
(df / da j) D ca j
представляет собой
частную погрешность результата косвенного измерения, вызван- ную погрешностью Δaj определения величины aj. Частные произ- водные df/daj называют коэффициентами влияния соответствую- щих погрешностей.
Оценим случайную погрешность результатов косвенных изме- рений. Пусть величины aj измерены со случайными погрешностя-
ми D& a j
, имеющими нулевые математические ожидания
M & [ D& a j ] = 0 и дисперсии s
[ D& ]. Запишем выражения для матема-
тического ожидания M [ D& ] и дисперсии s 2 [ D& ] погрешности D&:
m æ df
M [D] = åç da
÷ M [D aj ]= 0;
 &
&
j =1
ç ÷ &
|
m æ df ö

 m df df
m df df
2 ç÷ 2
s [ D& ] = å ç da ÷ s
j + å rkj
da
- s ks j,
da
j =1è j ø
k <1 k j
где ρkj – коэффициент корреляции погрешностей D& k
и D& j.
Если погрешности D& k
и D& j, некоррелированы, то ρkj=0 и
m æ df ö
|
j =1 j
(1.31)
è ø
Таким образом, для оценки результата z косвенного измере- ния следует использовать формулу (1.29), а для оценки система- тических и случайных погрешностей – соответственно (1.30) и (1.31).
Заметим, что в общем случае при нелинейной функции ко- эффициенты влияния df/daj, присутствующие в этих формулах, в свою очередь являются функциями значений величин aj. Ко- эффициенты влияния обычно оцениваются путем подстановки в выражения частных производных оценок aj. Следовательно, вместо самих коэффициентов влияния получают лишь их оценки. Кроме того, иногда коэффициенты влияния определя- ют экспериментально. В том и другом случае они устанавли- ваются с некоторой погрешностью, что является еще одним источником погрешности при обработке результатов косвен- ных измерений.
|
|
|
Суммарную составляющую случайной погрешности косвен- ного измерения можно упростить, если пренебречь погрешностя- ми, имеющими малые значения. Согласно критерию «ничтожной погрешности», если меньшая по значению случайная погреш- ность δ2 втрое меньше по значению большей по значению δ1, т.е. δ2 < 0,3 δ1, то ею можно пренебречь.
1.11. Суммирование погрешностей
При измерениях может быть несколько источников как систе- матических, так и случайных погрешностей. Поэтому практически важным является вопрос о правилах нахождения суммарной по- грешности измерения по известным значениям погрешностей со- ставляющих ее частей. При суммировании составляющих неис- ключенной систематической погрешности их конкретные реализа- ции можно рассматривать как случайные величины. Если известны границы Δi составляющих неисключенной систематической по- грешности, а распределение этих составляющих в пределах границ равномерно, то граница неисключенной систематической погреш- ности результата измерения вычисляется по формуле (1.26).
При суммировании случайных погрешностей необходимо учитывать их корреляционные связи. Суммарную среднеквадра- тичную погрешность при двух составляющих можно вычислить по формуле
s å =
s 1 + s 2 + 2 rs 1 s 2,
(1.32)
 2 2
2 2
где ζ1 и ζ2 – среднеквадратичные погрешности отдельных состав- ляющих; ρ – коэффициент корреляции.
|
|
|
Поскольку на практике трудно получить корректную оценку коэффициента ρ, приходится ограничиваться крайними случаями, т. е. считать, что либо ρ = 0, либо ρ = ±1. Тогда приведенная выше формула примет вид:
 2 2,
2 2,
s å =
или
s 1 + s 2
если ρ=0 (1.33)
| 2 2 |
s å = s 1 + s 2
,если ρ= 0±1. (1.34)
Таким образом, при отсутствии корреляционной связи средне- квадратичные погрешности складываются геометрически, а в слу-
чае жесткой корреляционной зависимости – алгебраически. Этот вывод справедлив и для случая нескольких источников погрешно- стей. При суммировании независимых погрешностей различных составляющих надо пользоваться критерием «ничтожной погреш- ности», который позволит значительно упростить вычисления. Из этого критерия следует, что группа погрешностей отбрасывается, если их сумма меньше одной трети максимальной погрешности.
Правила нахождения границы погрешности результата изме- рения при одновременном наличии как неисключенных система- тических, так и случайных погрешностей также регламентируют-
ся ГОСТ 8.207–76 и заключаются в следующем. Если
aн.с. < 0, 8,
 s S
s S
то неисключенными систематическими погрешностями по срав- нению со случайными пренебрегают и принимают, что граница погрешности результата:
Δ S = Δ & = | t(n)| Pдовs S, (1.35)
где
| t(n)| Pдовs S
– коэффициент Стьюдента, определяемый по
таблицам.
Если
aн.с. > 8, то, наоборот, пренебрегают случайной по-
 s S
s S
грешностью по сравнению с систематической и считают, что гра- ница погрешности результата DS = aн.с.
Если эти неравенства не выполняются, следует найти компо- зицию распределения случайных и неисключенных систематиче- ских погрешностей, рассматриваемых как случайные величины, вычислить значение среднеквадратичного отклонения и затем границы суммарной погрешности результата измерения при по- мощи приведенных в ГОСТ 8.207–76 эмпирических формул.
1.12. Формы записи результатов измерений
Результат измерения пригоден для дальнейшего использова- ния лишь тогда, когда помимо измеренного значения физической величины в нем указывается и значение погрешности. Производ- ственные измерения проводят обычно однократно, и точность полученного результата оценивают по нормируемым метрологи- ческим характеристикам используемых средств измерения.
|
|
|
Вычисляться должны как абсолютные, так и относительные погрешности результата измерения, так как первая из них нужна для округления результата и его правильной записи, а вторая – для однозначной сравнительной характеристики его точности.
В общем случае суммарная погрешность измерения будет со- держать систематическую и случайную составляющие:
Δ = Δс + Δ &.
(1.36)
Если не произведено разделение погрешностей на системати- ческие и случайные, то результат измерения (в соответствии с ГОСТ 8.011–72 «Показатели точности и формы представления результатов измерений») записывают в виде х, Δ от Δ ниждо Δверх, Р, где х – результат измерения в единицах из- меряемой величины; Δ от Δ ниж= Δ г.ниж, Δверх=Δг.верх– соответственно погрешность измерения с нижней и верхней ее границами; Р – вероятность.
Результаты многократных наблюдений, полученные при прямых измерениях физической величины, называются равноточными (рав- норассеянными), если они являются независимыми, одинаково рас- пределенными случайными величинами. Измерения в этом случае проводятся одним наблюдателем в одинаковых условиях внешней среды и с помощью одного и того же средства измерения.
Точную оценку действительного значения измеряемой вели- чины при равноточных измерениях можно получить лишь путем статистической обработки группы результатов измерений.
Конечный результат измерений согласно ГОСТ 8.011–72 представляется в одной из четырех форм:
1) интервалом, в котором с установленной вероятностью находится суммарная погрешность измерения;
2) интервалом, в котором с установленной вероятностью находится систематическая составляющая погрешности, стан- дартной аппроксимацией функции распределения случайной со- ставляющей погрешности измерения и среднеквадратичным от- клонением случайной составляющей погрешности измерения;
3) стандартными аппроксимациями функции распределения систематической и случайной составляющих погрешности изме- рения и их среднеквадратичными отклонениями;
|
|
|
4) функциями распределения систематической и случайной составляющих погрешности измерения.
Выбор формы представления результата измерения определя- ется назначением измерений и характером использования их ре- зультатов.
При записи результата измерения и погрешности младшие разряды числовых значений результата измерения и числовых значений погрешности должны быть одинаковыми.
Контрольные вопросы
1. Что изучает метрология?
2. Какие существуют методы измерений?
3. Какие бывают виды измерений?
4. Какие существуют погрешности измерений?
5. Что такое метрологические характеристики СИ?
6. Что понимают под единством измерений?
7. Как производится суммирование погрешностей СИ?
8. Приведите классификацию погрешностей СИ.
ГЛАВА 2. ТЕХНИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЙ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
2.1. Электромеханические измерительные приборы
Электромеханические измерительные приборы (ЭИП) от- личаются простотой, дешевизной, высокой надежностью, разно- образием применения, относительно высокой точностью.
Любой ЭИП состоит из ряда функциональных преобразовате- лей, каждый из которых решает свою элементарную задачу в цепи преобразований. Так, самый простейший измерительный электро- механический прибор прямого преобразования (вольтметр, ампер- метр) состоит из трех основных преобразователей: измерительной цепи (ИЦ), измерительного механизма (ИМ) и отсчетного устрой- ства (ОУ) (рис. 2.1).
Измерительная цепь обеспечивает преобразование электри- ческой измеряемой величины X в промежуточную электрическую величину Y (ток или напряжение), функционально связанную с измеряемой величиной и непосредственно воздействующую на измерительный механизм.
|
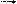
Рис. 2.1. Структурная схема электромеханического измерительного прибора прямого преобразования
Измерительный механизм является электромеханическим преобразователем, осуществляющим преобразование электриче- ской величины Y в наглядное аналоговое показание – угол α.
На магнитном воздействии электрического тока основаны магнитоэлектрический, электромагнитный, индукционный, элек- тродинамический и вибрационный измерительные механизмы.
Тепловое воздействие электрического тока используют биме- таллический и тепловой измерительные механизмы. На взаимо- действии заряженных электродов, находящихся под напряжени- ем, основан принцип работы электростатического измерительно- го механизма.
|
|
|
Отсчетное устройство состоит из указателя, жестко связан- ного с подвижной частью ИМ, и неподвижной шкалы. Указатели бывают стрелочные (механические) и световые.
Шкала – это совокупность отметок в виде штрихов, располо- женных вдоль линии, по которым определяют числовое значение измеряемой величины. Шкалы градуируют в единицах измеряе- мой величины – именованная шкала, либо в делениях – неимено- ванная шкала. В общем случае на подвижную часть ИМ при ее движении воздействуют моменты: вращающий М вр, противодей- ствующий М при успокоения М усп.
Вращающий момент М врдля ИМ, использующих силы элек- тромагнитного поля:
M вр= dW м/ dα, (2.1)
где dW м– изменение запаса энергии магнитного поля; α – угол отклонения подвижной части.
Противодействующий момент М пр в электромеханических приборах необходим для создания однозначного соответствия измеряемой величины определенному углу отклонения подвиж- ной части. В аналоговых электромеханических приборах проти- водействующий момент создается либо при помощи спиральных пружин (растяжек и подвесов), либо за счет энергии электромаг- нитного поля (в логометрах).
В случае, когда противодействующий момент создается спи- ральной пружинкой:
M пр= W α, (2.2)
где W α– удельный противодействующий момент, зависящий от геометрических размеров и материала пружины (растяжек).
Момент успокоения М успявляется моментом сил сопротивле- ния движению, направлен всегда навстречу движению подвиж- ной части ИМ и пропорционален угловой скорости отклонения:
M усп= P (dα/dt), (2.3)
где Р – коэффициент успокоения (демпфирования).
В измерительных механизмах наиболее часто применяют магнитоиндукционные и воздушные успокоители. Для созда- ния очень большого успокоения применяют жидкостные успо- коители.
Несмотря на большое разнообразие конструкций и типов при- боров все они имеют ряд общих узлов и деталей. Такими деталя- ми являются: корпус, шкала, указатель, устройства для установки и уравновешивания подвижной части, создания противодейству- ющего момента и успокоения, корректор, а в высокочувствитель- ных приборах – арретир.
Магнитоэлектрические приборы. Магнитоэлектрические приборы (МЭП) состоят из измерительной цепи, измерительного механизма и отсчетного устройства (см. рис. 2.1). Конструктивно измерительный механизм может быть выполнен либо с подвиж- ным магнитом, либо с подвижной катушкой. На рис. 2.2 показана конструкция прибора с подвижной катушкой. Постоянный маг- нит 1, магнитопровод с полюсными наконечниками 2 и непо- движный сердечник 3 составляют магнитную систему механизма. В зазоре между полюсными наконечниками и сердечником со- здается сильное равномерное радиальное магнитное поле, в кото- ром находится подвижная прямоугольная катушка 4, намотанная медным или алюминиевым проводом на алюминиевом каркасе (применяют и бескаркасные рамки). Катушка (рамка) 4 может поворачиваться в зазоре на полуосях 5 и 6. Спиральные пружины
7 и 8 создают противодействующий момент и используются для подачи измеряемого тока от выходных зажимов прибора в рамку (механические и электрические соединения на рис. 2.2 не показа- ны). Рамка жестко соединена со стрелкой 9. Для балансировки подвижной части имеются передвижные грузики 10.
Запас электромагнитной энергии в контуре с током I, находя- щемся в поле постоянного магнита, выражается формулой
W м= IΨ, (2.4)
где Ψ – полное потокосцепление данного контура с магнитным полем постоянного магнита.
 4 5
4 5
S N
1
9 2 6 3 2
7
8
10
Рис. 2.2. Схема устройства магнитоэлектрического прибора:
1 – постоянный магнит; 2 – полюсные наконечники; 3 – неподвижный сердечник; 4 – прямоугольная катушка; 5, 6 – полуоси, 7, 8 – спиральные пружины; 9 – стрелка; 10 – передвижные грузики
Тогда выражение (2.1) можно представить как
M вр= I dΨ/dα. (2.5)
Полное изменение потокосцепления с рамкой через конструк- тивные параметры рамки запишется следующим образом:
dΨ = B S w dα,
где В – индукция в зазоре; S – площадь рамки; w – число витков рамки.
Если положить dα = 1 рад, то произведение BSw – величина постоянная для каждого данного прибора и равная изменению
потокосцепления при повороте рамки на 1 рад. Обозначая его через Ψ0 запишем:
Ψ0 = BSw.
Тогда:
dΨ0 = Ψ0 dα. (2.6)
Подставляя выражение (2.6) в формулу (2.5), получим выра- жение вращающего момента для магнитоэлектрического меха- низма в следующем виде:
М вр= I Ψ0. (2.7)
Установившееся положение подвижной части ИМ наступает при равенстве вращающего и противодействующего моментов М вр= М пр, т.е. с учетом формулы (2.2) запишем:
I Ψ0 = W α.
Следовательно, уравнение преобразования для магнитоэлек- трического ИМ будет иметь вид:
α = I Ψ0 / W, или α =SII, (2.8)
где SI – чувствительность измерительного механизма по току, рад/А, SI= Ψ0/ W.
Также можно записать формулу (2.8) через конструктивные параметры измерительного механизма:
α = BSw I/W. (2.9)
Из формулы (2.9) следует, что угол отклонения подвижной части ИМ прямо пропорционален току в катушке, поэтому маг- нитоэлектрические приборы имеют равномерные шкалы.
В магнитоэлектрических приборах успокоение подвижной ча- сти приборов магнитоиндукционное, т.е. создается взаимодей- ствием магнитных полей от вихревых токов в каркасе катушки и поля постоянного магнита.
Д о с т о и н с т в а: высокий класс точности – 0,05 и ниже, рав- номерная шкала, высокая и стабильная чувствительность, малое собственное потребление мощности, большой диапазон измере-
ний, на показания МЭП не влияют внешние магнитные и элек- трические поля.
Н е д о с т а т к и: без преобразователей МЭП используют толь- ко в цепях постоянного тока, имеют малую нагрузочную способ- ность, сложны и дороги, на их показания влияют колебания тем- пературы.
П р и м е н е н и е: магнитоэлектрические ИМ используют в амперметрах, вольтметрах, омметрах и гальванометрах (обыч- ных, баллистических и вибрационных).
Амперметры. Магнитоэлектрический измерительный меха- низм, включенный в электрическую цепь последовательно с нагрузкой, позволяет измерять токи порядка 20...50 мА. Для рас- ширения пределов измерения используют шунты (манганиновый резистор), сопротивление которых мало зависит от температуры. Сопротивление шунта R шменьше сопротивления прибора R при выбирается из соотношения:
R ш= R пр / (n - 1), (2.10)
где n – коэффициент шунтирования по току, n=I/I пр.
Вольтметры. Магнитоэлектрический измерительный меха- низм, включенный параллельно нагрузке. Для расширения преде- лов измерения по напряжению последовательно с ИМ включают добавочный резистор R доб, сопротивление которого больше со- противления R пp:
R доб= R пр / (m - 1), (2.11)
где m – коэффициент шунтирования по напряжению, m=U/U пр.
Логометры. Приборы электромеханической группы, измеря- ющие отношение двух электрических величин, обычно двух то- ков α= f (I1/I2), что позволяет сделать их показания независимыми в известных пределах от напряжения источника питания. В лого- метрах вращающий и противодействующий моменты создаются
электрическим путем и направлены навстречу друг другу. На рис.2.3 приведена схема устройства магнитоэлектрического ло- гометра.
В поле постоянного магнита помешена подвижная часть, со- стоящая из двух жестко закрепленных под определенным углом рамок. Особой формой полюсных наконечников и сердечника, находящегося между ними, искусственно создается неравномер- ное магнитное поле постоянного магнита. Токи к рамкам подво- дятся через безмоментные токоподводы, не создающие противо- действующего момента.
Направления токов в рамках логометра выбираются так, что- бы моменты М вр, и М прбыли направлены в разные стороны. Тогда в общем виде можно записать
М вр= I1 f1 (α); М пр = I2 f2 (α), (2.12)
где I 1 и I 2 – токи в рамках; α – угол отклонения подвижной части от некоторого условного нулевого положения.







 3
3
N S
Рис. 2.3. Схема устройства магнитоэлектрического логометра
Равновесие подвижной части наступает при равенстве момен- тов М ври М пр, действующих на рамку, т.е. при условии I1f1( α ) = I2f2 (α).
Откуда:
I1/ I2 = f2 (α) / f1( α ) = f( α )
или:
α = F (I1/ I2). (2.13)
 r2 r1
r2 r1
r2 r1
E E
r0 rx
r0 r3
 а б
а б
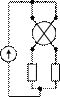
Рис. 2.4. Схемы устройства магнитоэлектрических омметров с логометрическим механизмом для измерения больших (а)
и малых (б) сопротивлений
Омметры. Магнитоэлектрические логометры широко приме- няются в приборах для измерения сопротивления – омметрах и мегоомметрах, в выпрямительных частотомерах и устройствах для измерения неэлектрических величин (температуры, давления, уровня жидкости и др.).
На рис. 2.4 приведены схемы магнитоэлектрических оммет- ров с последовательным (рис. 2.4, а) и с параллельным (рис. 2.4, б) включением измеряемого сопротивления. Последовательное включение применяется при измерении средних и больших со- противлений, параллельное – при измерении малых сопротив- лений.
При последовательном включении (см. рис. 2.4, а) токи в ка- тушках:
I1 = E /(r1+r0); I2 = E /(r2+rx),
где E – напряжение питания; r1 и r2 – сопротивления обмоток ра- мок; r0, r3 – известные сопротивления; rx – неизвестное сопротив- ление.
Тогда согласно выражению (2.13) уравнение преобразования запишется в виде:
α = F [(r2+rx) / (r1+r0)]. (2.14)
Из формулы (2.14) видно, что независимо от величины напря- жения питания Е и при постоянных r1 r2 и r0 отклонение подвиж- ной части является однозначной функцией rx и шкала прибора может быть проградуирована в единицах сопротивления.
В приборах с параллельным включением (см. рис. 2.4, б) при постоянном напряжении питания Е ток I1 не зависит, а ток I2 за- висит от rx. Отношение токов, а следовательно, и угол α не зави- сят от напряжения питания и являются однозначной функцией rx, т.е. и здесь шкала может быть проградуирована в омах. Обе схемы обычно объединяют в одном приборе – омметре, переход от одной схемы к другой осуществляется с помощью переклю- чателя.
Логометрические омметры – приборы невысокого класса точ- ности (1,5; 2,5; 4,0). Погрешность омметра указывается в процен- тах от длины рабочей шкалы.
Аналогично рассмотренному принципу построения логомет- рического ИМ магнитоэлектрической системы выпускают лого- метры электромагнитной, электродинамической, ферродинами- ческой и индукционной систем.
Гальванометры постоянного тока. На рис. 2.5 показана схе- ма устройства магнитоэлектрического гальванометра постоянно- го тока.
Сильный постоянный магнит 2 из высококоэрпетивного спла- ва, полюсные наконечники 5 из магнитомягкой стали с цилин- дрической расточкой концов и неподвижный стальной цилиндр 7, укрепленный в расточке, служат для создания в зазоре сильного равномерного магнитного поля. В этом зазоре находится рамка 4, укрепленная на подвесе 1, к которой через безмоментные токо-
подводы 6 подводится ток. На оси рамки закреплено зеркальце 3 для оптического отсчета угла отклонения рамки от нулевого по- ложения.
 1
1
2
3
4
5
7
6 6
Рис. 2.5. Схема устройства магнитоэлектрического гальванометра:
1 – подвес; 2 – постоянный магнит; 3 – зеркальце; 4 – рамка; 5 – полюсные наконечники; 6 – безмоментные токопроводы; 7 – стальной цилиндр
На рамку при подаче тока I действуют моменты: вращающий М вр, вычисляемый по формуле (2.1), противодействующий М пр, создаваемый при закручивании подвеса и вычисляемый по фор- муле (2.2), и успокоения М усп, вычисляемый по формуле (2.3).
Величина Р = Ψ0 /(R г + R вн) называется коэффициентом успо- коения и определяется конструктивными параметрами гальвано- метра – Ψ0, R ги сопротивлением внешней цепи R вн. Изменяя R вн, можно изменять коэффициент успокоения.
Известно, что движение вращающегося тела определяется уравнением:
2 a
 J d dt 2
J d dt 2
= å M,
где J – момент инерции тела; d2α /dt2 – угловое ускорение; å M – сумма вращающих моментов, действующих на тело.
Для гальванометра это уравнение имеет вид:
d 2 a
 J dt 2
J dt 2
= Mвр + Мпр + М усп. (2.15)
Подставляя в выражение (2.15) значения моментов с учетом их знака, получим дифференциальное уравнение движения по- движной рамки гальванометра:
|
|
|


