Групповые формы работы как средство реализации ФГОС

Совершенствование учебного процесса идет сегодня в направлении увеличения активных методов обучения, обеспечивающих глубокое проникновение в сущность изучаемой проблемы, повышающих личное участие каждого обучающегося и его интерес к учению.

Федеральный государственный образовательный стандарт четко определяет понятие и структуру групповой работы. Так, В. К. Дьяченко под групповой работой понимает «организационную форму коллективной работы, при которой три и более обучающихся одновременно осуществляют совместную деятельность, направленную на решение поставленной задачи» [17, с. 12].

Н. Е. Щуркова определяет групповую работу следующим образом: «Групповая работа – это форма организации учебно-познавательной деятельности на уроке, предполагающая функционирование разных малых групп, работающих как над общими, так и над специфическими заданиями педагога, стимулирует согласованное взаимодействие между обучающимися, отношения взаимной ответственности и сотрудничества» [50, с. 5].

По мнению известного психолога И. Н. Семенова [43], групповая работа – спектр деятельности, включающий метод социального вмешательства, с помощью которого отдельные индивиды и группы могут развить навыки решения проблем для преодоления возникших затруднений и проблем участников группы. Оценка метода групповой работы основана преимущественно на субъективных отзывах участников, наблюдениях лидеров группы и фасилитаторов. Отзывы свидетельствуют о возможной эффективности группового подхода во всех сферах социальной работы. Принято считать, что группа влияет на поведение и установки индивида, однако это не означает, что сформированные группы достигнут своих целей.

Во всех вышеуказанных определениях говорится о том, что создаются небольшие группы учащихся, объединенные для выполнения общего задания.

В работах Н. Е. Щурковой [50] приведены основные приёмы групповой работы, которые в последнее время активно используются на уроках математики (рисунок 3).

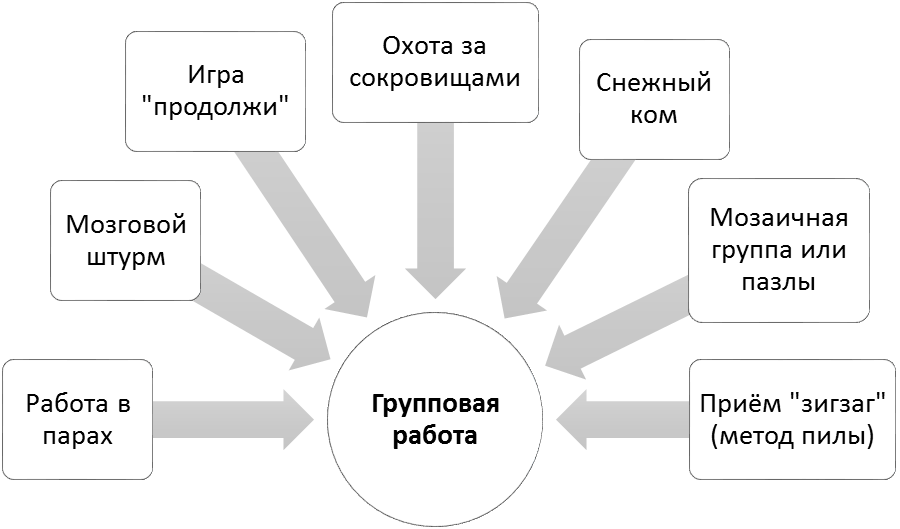
Рисунок 1. Приёмы групповой работы

(по Н. Е. Щурковой)

 

Более детально рассмотрим каждый из приёмов организации групповой работы, применяемых сегодня на уроках математики.

1.Приём мозговой штурм основывается на:

– генерации идей;

– соблюдении жесткого регламента;

– распределения роли внутри группы (ведущего, секретаря, хронометриста);

– после выработки коллективного решения внутри группы делаются доклады/сообщения от разных групп.

2.Приём игра «Продолжи» основан на выполнении заданий разного рода группой «по цепочке», т.е. одно за одним.

Можно использовать на уроках по разным предметам (например, на уроке математики на этапе актуализации знаний при устном счёте, при написании сочинения по русскому языку, на уроке природоведения при составлении рассказа о каком-либо животном, на уроке истории при составлении обзора исторических событий и др.).

3.Приём охота за сокровищами состоит в следующем. Учитель составляет вопросы. Вопросы могут требовать как знаний фактов, так и осмысления или понимания. Обучающийся или группа учеников должны ответить на вопросы, используя ресурсы интернета, дополнительную литературу, учебник.

4. Приём снежный ком направлен на развитие у обучающихся навыков адекватного реагирования на проблемы, совместного решения установленных проблем, обобщения и систематизации мнений окружающих.

Кроме того, приём особенно эффективен в работе с учениками, у которых слабо развиты коммуникативные навыки, и побуждает их высказывать свое мнение сначала в условиях парной работы, а затем в работе больших групп. Данный приём позволит учителю выслушать мнения всех учеников в отношении поставленного вопроса и достичь единого мнения всего класса без общего обсуждения.

Приведём один из вариантов реализации данного приёма. Он состоит в работе в группе, которая начинается с решения индивидуального задания. Все учащиеся получают аналогичные задания и самостоятельно выполняют их.

После этого следует работа в парах. В парах обучающиеся предлагают свои способы решения данного задания, из которых выбирается лучшее.

Далее две пары объединяются, и работа продолжается в группе из четырех человек, где снова происходит обсуждение решений и выбирается лучшее из них.

В конце работы все учащиеся попадают в одну группу. На этом последнем этапе уже не происходит обсуждения решений, группы делают доклады о своей работе.

5. Приём мозаичная группа или пазлы имеет следующую структуру. Учитель делит тему на несколько частей так, чтобы каждая группа получила бы свою часть темы. Также все группы получают список необходимых источников или сами учебные материалы, с помощью которых они изучают основы предложенной части темы.

После изучения материала или выполнения задания группы переформируются так, чтобы в каждую новую группу попали по одному человеку от каждой прежней группы. Каждый член новой группы объясняет своим новым коллегам свою часть темы, основы которой он изучил в составе предыдущей группы и отвечает на заданные вопросы. В заключение работы делают выводы.

6. Приём зигзаг (метод пилы) один из самых сложных в реализации на уроках математики. Его структура заключается в следующем. Новая тема изначально делится учителем на несколько частей. Класс делится на группы с равным количеством участников. Для удобства будем называть эти первичные группы рабочими. Материал должен быть поделен на столько частей, сколько участников в этой первичной группе. Каждая группа получает один и тот же новый материал. Причем каждый участник рабочей группы получает по одному отрывку из текста темы. Эти отрывки можно пронумеровать или отметить разными цветами.

Индивидуальная работа. Каждый ученик работает со своей частью темы, прорабатывает информацию, анализирует, составляет опорный конспект. Важно, чтобы из отрывка было взято все самое нужное. Задача ученика: представить своеобразную «выжимку», квинтэссенцию. Причем сделать это он может по-разному – составить кластер, таблицу, схему, инфографику и т.д.

Следующий этап работы – групповой. Теперь обучающиеся переходят к своим «коллегам». Составляются экспертные группы. То есть, в одной команде окажутся все те, кто получил отрывок № 1, в другой – те, кто получил отрывок № 2. Начинается этап обсуждения. Обучающиеся обмениваются своими работами, мнениями, выбирают самый лучший вариант для презентации своей части текста. Дополнительным заданием может быть составление вопросов по своему отрывку, которые покажут, насколько остальные поняли и усвоили материал. Причем вопросы тоже можно разнообразить – либо это просто вопросы, либо мини-тесты, либо какое-то практическое задание. После этого ученики возвращаются в свои рабочие группы, и начинается этап размышления. Каждый по очереди презентует свою часть текста. Будет это краткое изложение, кластер, таблица – это решено уже на стадии работы в экспертной группе. Таким образом, каждый из учеников получает сведения по всему тексту новой темы. Завершается «Зигзаг» общей работой всего класса. Каждую часть темы презентует один из экспертов по данному вопросу. В итоге происходит вторичное прослушивание материала. Остальные эксперты «дополняют» коллегу.

На этапе рефлексии обучающиеся решают, чья презентация материала была наиболее точной и эффективной. А также намечают круг вопросов, которые требуют уточнений, пояснений. Итогом такой работы может стать совместный проект или презентация. На основе рассмотренных приёмов можно сделать вывод, что каждый из них по-своему интересен и вносит новизну в учебный процесс. Выбор наилучшего приёма, который впишется в современный урок, остаётся за учителем.

Организовывая групповую работу на уроках математики, можно использовать различные варианты комплектования групп. Ведь разделение класса на группы – это важный момент в организации работы. Способов разделения существует множество, и они в значительной степени определяют то, как будет протекать дальнейшая работа в группе, и на какой результат эта группа выйдет [28].

1. Разделение «по желанию»

Объединение в группы происходит по взаимному выбору. Задание на формирование группы по желанию может даваться, как минимум, в двух вариантах:

– разделитесь на группы по... человек;

– разделитесь на... равные группы.

2. Распределение «случайным образом»

Группа, формируемая по признаку случайности, характеризуется тем, что в ней могут объединяться (правда, не по взаимному желанию, а волей случая) дети, которые в иных условиях никак не взаимодействуют между собой либо даже враждуют. Работа в такой группе развивает у участников способность приспосабливаться к различным условиям деятельности и к разным деловым партнерам.

Этот способ формирования групп полезен в тех случаях, когда перед учителем стоит задача научить детей сотрудничеству. Данный способ также может использоваться в классах, в которых между учениками сложились в целом доброжелательные отношения. Но в любом случае педагог должен обладать достаточной компетентностью в работе с межличностными конфликтами.

Способы формирования «случайной» группы: жребий; объединение тех, кто сидит рядом (в одном ряду, в одной половине класса); с помощью импровизированных «фантов» (один из учеников с закрытыми глазами называет номер группы, куда отправится ученик, на которого указывает в данный момент педагог) и т.п.

3. Распределение «по определённому признаку»

Такой «признак» задается либо учителем, либо любым учеником. Так можно разделиться по первой букве имени (гласная – согласная), в соответствии с тем, в какое время года родился (на четыре группы), по цвету глаз (карие, серо-голубые, зеленые) и так далее.

Этот способ деления интересен тем, что, с одной стороны, может объединить детей, которые либо редко взаимодействуют друг с другом, либо вообще испытывают эмоциональную неприязнь, а с другой – изначально задает некоторый общий признак, который сближает объединившихся учащихся. Есть нечто, что их роднит и одновременно отделяет от других. Это создает основу для эмоционального принятия друг друга в группе и некоторого отдаления от других (по сути дела – конкуренции).

4. Распределение «по выбору лидера»

«Лидер» в данном случае может либо назначаться учителем (в соответствии с целью, поэтому в качестве лидера может выступать любой ученик), либо выбираться детьми. Формирование групп осуществляется самими «лидерами». Например, они выходят к доске и по очереди называют имена тех, кого они хотели бы взять в свою группу. Наблюдения показывают, что в первую очередь «лидеры» выбирают тех, кто действительно способен работать и достигать результата. Иногда даже дружба и личные симпатии отходят на второй план.

В том случае если в классе есть явные аутсайдеры, для которых ситуация набора в команду может быть чрезвычайно болезненной, лучше или не применять этот способ, или сделать их «лидерами».

5. Распределение «по выбору педагога»

В этом случае учитель создает группы по некоторому важному для него признаку, решая тем самым определенные педагогические задачи. Он может объединить учеников с близкими интеллектуальными возможностями, со схожим темпом работы, а может, напротив, создать равные по силе команды. При этом организатор групповой работы может объяснить принцип объединения, а может уйти от ответа на вопросы участников по этому поводу.

Также существуют ещё несколько вариантов разделения класса на группы, таких как разделение по теме предстоящей работы и по уровню сложности задания. Но их применение менее эффективно на уроках математики, и они уже частично включены в варианты разделения, представленные выше.

Таким образом, можно сделать вывод, что в своей сущности групповая работа предполагает включение группы обучающихся в совместное планирование учебной деятельности, восприятие и уяснение информации, обсуждение, взаимный контроль. Ведь такая организация работы чрезвычайно эффективна и современна на сегодняшний день, она отвечает потребностям как школьников, так и учителей, и соответствует требованиям, которые предъявляет ФГОС.

 

1.2 Функции коммуникативных УУД и особенности их развития
у обучающихся 5 классов при обучении математике

 

Обучающиеся 5 классов общеобразовательной школы находятся в подростковом периоде развития, который занимает особое положение в цикле развития, что отображается в его характеристике как «трудного», «переходного». Границы подросткового возраста захватывают период от 11 вплоть до 14-15 лет. Основное содержание подросткового возраста составляет начало перехода с детства к взрослости. Это отображается в развитии элементов взрослости в физиологическом, общественном, интеллектуальном, эмоционально-личностном развитии подростка. Именно на подростковый возраст приходятся сложные процессы перестройки организма, формирования самосознания, развитие нового вида отношений с окружающими, интеллектуального развития и становления нравственно-этических инстанций, опосредующих поведение, деятельность и отношения [22].

Согласно Гальперину П. Я., возрастные кризисы в 12-15 года связаны с развитием коммуникативных навыков личности, принципиально изменяющим характер ее развития: от развития «по общественному проекту» подросток переходит к саморазвитию. Это решающим образом меняет вид учебной деятельности и социальную ситуацию развития – систему значимых социальных и межличностных взаимоотношений школьника. Изменяются коммуникативные отношения со взрослыми, подросток начинает сопротивляться требованиям, которые раньше с удовольствием выполнял; обижается и протестует, когда ограничивают его независимость. В следствии права взрослых он ограничивает, а собственные расширяет и претендует на признание его личности, равноправие с взрослыми. В то же время развиваются более глубокие коммуникативные взаимоотношения со сверстниками. У подростка формируются ценности, которые более понятны и близки сверстнику, чем взрослым [10].

Наряду с коммуникациями собственное значение сохраняет и учебная деятельность, которая обретает черты деятельности согласно саморазвитию и самообразованию. В основной школе обучающиеся начинают овладевать высшими формами мыслительной деятельности – теоретическим, формальным, рефлексивным мышлением. У школьника появляется способность рассуждать гипотетико-дедуктивным методом, абстрактно-логическим. Содержанием подобного рассуждения являются выражения, требуемые для коммуникации [43].

Другая характерная особенность этого уровня мышления при коммуникации состоит в развитии рефлексии – способности делать предметы процессе общения центром внимания, анализа и оценки собственные умственные операции. Развитие теоретического мышления становится основой формирования нового вида коммуникативных взаимоотношений не только лишь к фактам, но и закономерностям [43].

В силу данных причин, а кроме того с учётом требований ФГОС, перед учителями, преподающими в 5 классах, особенно значимо стоит вопрос развития не только предметных навыков обучения, но и метапредметных, включающих в себя формирование коммуникативных навыков личности в социуме, развитие самостоятельности и моральных устоев. При помощи развёртывание учебно-проектных ситуаций развития и создание событийной общности обеспечивается возможность поддержки стремления школьников к самореализации и утверждению нового статуса взрослости в ходе коммуникации; освоение обучающимися проектированием как методом познания мира и на данной основе – полной нормативной структурой учебной деятельности. Это призывает изменения формы организации учебной деятельности и учебного сотрудничества при обучении математике

– с классно-урочной к лабораторно-семинарской и к лекционно-лабораторной исследовательской [44].

Овладение обучающимися универсальными учебными действиями в ходе коммуникации происходит в контексте различных учебных предметов, том числе и математике. Разумеется, что чёткой границы по формированию определённого типа УУД в процессе изучения математики отсутствует и не может быть. Однако, перенос акцентов возможен. В одних темах может уделяться большое внимание формированию одних разновидностей УУД, в иных – в формирование других УУД [30].

Коммуникативные универсальные учебные действия в отличие, в частности, с других УУД, связаны с методами организации учебно-воспитательного процесса, а никак не с содержанием обучения. Для овладения коммуникативных УУД нужны операции, отличающиеся от освоения математических знаний. Обучающийся 5 класса постигает коммуникативные УУД через включенность в необходимую деятельность и дальнейшую рефлексию собственных действий. Работа по формированию коммуникативных УУД проводится в ходе освоения математических знаний при применении специальных разновидностей деятельности с предметным содержанием и за счет изменения способов сотрудничества обучающихся. Важным содержательным материалом являются математические знания и умения.

 

Коммуникативные УУД согласно А. Г. Асмолову обладают функциями, проявляющимся в последующих нюансах:

– обучающий: владение диалогической и монологической формами речи в соответствии с грамматическим и синтаксическим нормам языком; обеспечение обменом знаний между членами группы с целью принятия продуктивных совместных решений; способность с помощью вопросов извлекать необходимую информацию; умение искать и обрабатывать информацию; умение высказывать свои идеи в устной и письменной форме; осознанное чтение;

– развивающий: ожидание различных вероятных мнений других людей; развитие способности к самосознанию и рефлексии;

– воспитательный: развитие критичности; способность брать инициативу на себя в организации группового действия; уважительное отношение к партнерам, внимание к личности другого; готовность правильно реагировать на потребности других; стремление устанавливать доверительные взаимоотношения и добиваться взаимопонимания; взаимовыручка в процессе выполнения задачи;

– социальный: восприятие возможности существования разных мнений, никак не схожих с личной; формулирование цели и ролей участников, способов сотрудничества; готовность к обсуждению разных точек зрения и выработке общей (коллективной) позиции; способность аргументировать свое мнение, спорить и бесконфликтно защищать свое мнение; умение создавать деловые взаимоотношения; формирование результативного сотрудничества с сверстниками и взрослыми; предоставление бесконфликтной коллективной работы в команде [40].

Основные типы коммуникативных, в том числе речевых действий, в силу своего действительно универсального, то есть максимально-обобщённого, характера в системе С. В. Молчанова, которые естественным способом распространяются на все учебные предметы и, в особенности, в внеурочную деятельность по математике. Потому как нет предметов, где обсуждения вопроса были бы неуместны, а работа обучающихся 5 классов в малых группах не требовала бы координации различных точек зрения в процессе достижения общего результата [26].

В концепции С. В. Молчанова [26] выделяются следующие функции коммуникативных операций:

-  планирование учебного сотрудничества с учителем и сверстниками – установление целей, функций участников, методов взаимодействия;

- постановка вопросов – инициативное сотрудничество в поиске и сборе данных;

- разрешение конфликтов – обнаружение, распознавание проблемы, поиск и анализ альтернативных методов разрешение конфликта, принятие решения и его реализация;

- управление поведением партнёра – контроль, корректировка, анализ действий партнёра;

- умение с достаточной полнотой и точностью представлять собственные мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими общепризнанными мерками родного языка [26].

Для развития коммуникативной компетенции огромное значение имеет учебно-методический комплект. Опираясь на исследования С. В. Молчанова, деятельность по развитию математической речи чётко выстроена во всех учебниках по математике и включает развитие широкого спектра навыков, предусматривает количественное и качественное обогащение словарного запаса учащихся, развитие связной устной и письменной математической речи.

Для развития коммуникативных УУД в 5 классе С. В. Молчанов предлагает обращать внимание на следующие функции:

 

- умение планировать работу группы на уроках математики и работать по плану;

- умение формулировать проблему при изучении темы по математике, высказывать свою точку зрения при доказательстве теорем и сопоставлять ее с точкой зрения других;

- готовность к обсуждению разных точек зрения и выработки общей позиции при обсуждении решения математических задач;

- умение довести диалог при введении новых математических терминов до логического завершения;

- отвечать на вопросы по прочитанному параграфу или прослушанной математической лекции;

- создавать устные монологические высказывания разного типа при обсуждении доказательств теорем;

- уметь вести диалог во время обсуждения решения задачи;

- умение взаимодействовать в ходе выполнения групповой работы, участвовать в дискуссии при работе над математическим проектом, аргументировать собственную точку зрения;

- овладение умениями работать в группе с выполнением заданий по раздаточному материалу, представлять и отстаивать свои взгляды и убеждения, вести дискуссию во время презентации, выполненной группой работы;

- уметь информировать о результатах своих наблюдений, участвовать в дискуссии, отстаивать свою точку зрения, находить компромиссное решение в различных ситуациях на уроке математики, на факультативе;

- использовать современные источники информации, в том числе материалы на электронных носителях, владение основами работы с учебной и внешкольной информацией, представлять результаты своей деятельности в различных формах (презентация, реферат и др.) [26].

– курсе математики можно выделить две взаимосвязанных особенности развития коммуникативных универсальных учебных действий:

- развитие устной математической речи;

- развитие комплекса умений, на которых базируется грамотное эффективное взаимодействие.

К первому направлению можно отнести все задания, содержащие задачи для изучения новой темы, задачи повышенной трудности.

Ко второму направлению развития коммуникативных универсальных учебных действий относится система задач, нацеленных на организацию общения учеников в паре или группе [31].

Знания особенностей развивающего обучения помогает созданию коммуникативных ситуаций во время урока математики, то есть благоприятных условий для активного общения. Форма взаимодействия демократична: совместное размышление над задачей, приближение учебного процесса к реальным жизненным ситуациям, обращение к опыту ученика. На уроках математики в 5 классе используются разные формы организации коммуникативного общения: работа в парах, групповые, индивидуально-групповые.

Итак, коммуникативные УУД обеспечивают общественную подготовленность и учет позиции других людей, партнера по общению или деятельности, способность слушать и вступать в диалог; принимать участие в коллективном обсуждении проблем; интегрироваться в группу сверстников и строить результативное взаимодействие и сотрудничество со сверстниками и взрослыми.

Видами коммуникативных действий на уроках математики в 5 классе являются:

- планирование учебного сотрудничества с учителем и сверстниками;

- определение целей, функций участников, способов взаимодействия в группе;

- постановка вопросов – инициативное сотрудничество в поиске и сборе данных;

- разрешение конфликтов – обнаружение, идентификация проблемы, поиск и анализ альтернативных методов разрешения конфликта, принятие решения и его осуществление;

- управление поведением партнера – контроль, коррекция, анализ действий партнера;

- умение с достаточной полнотой и точностью представлять свои идеи в соответствии с задачами и условиями коммуникации;

- владение монологической и диалогической формами выступления [13].

Для развития коммуникативных универсальных учебных действий, с учетом их особенностей, у учащихся 5 класса могут использоваться перечисленные ниже технологии обучения.

1. Технология интерактивного обучения математике: использование интерактивных технологий в работе учителя математики способствует повышению мотивации учащихся к обучению.

2. Информационно-коммуникационная технология обучения математике. Активное и эффективное внедрение ИКТ в процесс обучения математике позволяет:

- учителю математики успешнее работать над развитием и совершенствованием навыков математической устной и письменной речи у учащихся 5 класса;

- повысить мотивацию и познавательную активность за счет разнообразия форм групповой работы на уроках математики.

3. Технология проблемного обучения математике

Проблемное обучение на уроках математики имеет практическую значимость в формировании личности. Использование технологии проблемного обучения способствует развитию коммуникативных УУД, стимулирует интерес у обучающихся 5 класса, поддерживает высокую мотивацию к изучению предмета.

4. Метод проектов на уроке математики

Обучающимся 5 класса предлагается создать свои проекты по определенной теме и представить их в виде презентаций. Создавая проекты, ученикам предоставляется отличная возможность систематизации полученных знаний и навыков, а также возможность реализации интеллектуальных и творческих способностей, с учетом особенностей их развития [11].

С помощью перечисленных выше технологий обучения математике, направленной на развитие коммуникативных УУД обучающихся 5 класса, качественно улучшается процесс приобретения обучающимися знаний, развиваются речевые умения, за счет использования интерактивных компьютерных сред можно дифференцировать и индивидуализировать процесс обучения математике. Все это способствует развитию коммуникативных универсальных учебных действий обучающихся 5 класса при обучении математике.

Типовые задания на уроках математики для развития коммуникативных действий в 5 классе могут звучать так [39]:

- приведите пример того, что (как, где) …;

- придумайте игру, которая…;

- проведите презентацию…;

- выскажите критическое суждение о …;

- прокомментируйте положение о том, что…;

- изложите в форме… свое мнение… (понимание)…;

- объясните…

Особенности развития коммуникативных УУД у обучающихся 5 класса на уроках математики имеет особую значимость в образовательном процессе.

Во-первых, коммуникативная компетентность влияет на учебную успешность обучающихся: если ученик при ответе испытывает дискомфорт, тревогу, то его ответ будет хуже имеющихся знаний, при этом его оценка, соответственно, ниже. Полученный негативный ответ может сказаться на последующей учебной деятельности.

Во-вторых, от коммуникативной компетентности во многом зависит благополучие в классном коллективе. Если учащийся легко находит общий язык с одноклассниками, то испытывает психологический комфорт и удовлетворённость ситуацией. И напротив, неумение контактировать с ровесниками сужает круг друзей, вызывает ощущения неприятности, одиночества в классе, проявления враждебности и агрессии по отношению к сверстникам [32].

Основным критерием сформированности коммуникативных действий можно считать коммуникативные способности учащегося, включающие в себя:

- желание вступать в контакт с окружающими (мотивация общения «Я хочу!»);

- знание норм и правил, которым необходимо следовать при общении с окружающими;

- умение организовывать общение, включающее умение слушать собеседника, умение решать конфликтные ситуации [27].

Функции и особенности развития коммуникативных УУД обучающихся 5 класса при обучении математике обеспечивают не только развитие умений взаимодействовать с другими людьми, с объектами окружающего мира и его информационными потоками, отыскивать, преобразовывать и передавать информацию, выполнять разные социальные роли в группе и коллективе, но и является ресурсом эффективности и благополучия их будущей взрослой жизни.

 

123456

Поделиться:

Воспользуйтесь поиском по сайту: