Электромагнитные колебания

 

Электромагнитные колебания возникают в колебательном контуре, состоящем из конденсатора С и катушки индуктивности L. Электрическая схема контура приведена на рис. 24.

 

Рис. 24. Электрический колебательный контур

 

Если конденсатору сообщить заряд q, то конденсатор будет разряжаться через катушку индуктивности. Ток разрядки создает магнитное поле в катушке. В момент t = T /4 (здесь Т – период электромагнитных колебаний) энергия электрического поля обращается в нуль, а энергия магнитного поля достигает наибольшего значения. Начиная с этого момента, магнитное поле в катушке убывает, в ней индуцируется ток, который обеспечивает заряд конденсатора, имеющий противоположную полярность. В момент времени t = T /2 энергия магнитного поля обращается в нуль, а энергия электрического поля достигает наибольшего значения. Далее те же процессы начнут протекать в обратном направлении, и при t = T колебательный контур перейдет в первоначальное состояние. Подобным образом в контуре происходят колебания электрического заряда на обкладках конденсатора (с периодом Т), тока в цепи (с периодом Т) и энергий электрического и магнитного полей. В моменты t = 0, T /2, T энергия электрического поля максимальна, а энергия магнитного поля равна нулю; в моменты t = T /4, 3 T /4 энергия магнитного поля максимальна, а энергия электрического поля равна нулю.

Для свободных незатухающих гармонических колебаний в контуре, состоящем из индуктивности L и электрической емкости С (при R =0), записывается дифференциальное уравнение в виде

d ² q / dt ² + ω_o² q = 0,

где ω_o=(LC)^-1/2 – собственная частота незатухающих колебаний и, следовательно, период T _o = 2π(LC)^1/2 (формула Томпсона). Решением уравнения дифференциального уравнения является выражение:

q = q_msin (ω_o t + φ_o),

где q_m – амплитудное (максимальное) значение заряда конденсатора. При этом сила тока в контуре

I = dq / dt = I_msin (ω_o t + φ_o – π/2),

где I_m = ω_o q_m – амплитуда силы тока. Энергия электрического поля в конденсаторе

W _э= q ²/2 C = (q_m ²/2 C) sin ²(ω_o t + φ_o)

и магнитного поля в индуктивности контура

W _м= I ² L /2 = (I_m ² L /2) cos ²(ω_o t + φ_o)

могут также быть соответственно записаны в виде

W _э= (q_m ²/4 C)[1– cos 2(ω_o t + φ_o)],

W _м= (LI ²/4)[1+ cos 2(ω_o t + φ_o)].

Из приведенных соотношений следует, что W _э и W _м изменяются с частотой, в два раза превышающей собственную частоту колебаний в контуре.

Электромагнитные волны

 

Собственная циклическая частота электромагнитных колебаний в контуре определяется соотношением ω_o=(LC)^-1/2. Следовательно, при уменьшении электрической емкости С (например, путем увеличения расстояния между обкладками конденсатора) частота ω_o будет увеличиваться. Максимально раздвигая пластины конденсатора, можно получить открытый колебательный контур. В таком контуре электромагнитные колебания могут распространяться в пространстве. Электромагнитными волнами называется распространяющееся в пространстве переменное электромагнитное поле. Экспериментально электромагнитные волны впервые исследовал Герц. В качестве открытого колебательного контура он использовал два стержня с шариками на концах. К стержням подводилось переменное электрическое напряжение, шарики были разделены искровым промежутком. Такой электромагнитный вибратор способен излучать радиоволны с частотой порядка 10⁵ ÷ 10¹⁰ Гц. В ходе экспериментов Герц установил, что радиоволны подчиняются тем же законам отражения и преломления, что и световые волны (частоты световых волн 10¹³÷10¹⁵ Гц). Связь между векторами электрической E и магнитной H напряженностей в электромагнитной волне, распространяющейся в непроводящей среде, определяется уравнениями Максвелла.

Рассмотрим вновь колебательный контур. При воздействии на него переменной ЭДС в контуре устанавливаются вынужденные колебания. Амплитуда вынужденных колебаний тока при постоянных значениях L и C, а для неидеального контура еще и активного сопротивления R, зависит от соотношения собственной частоты колебаний контура и частоты изменения синусоидальной ЭДС. Электрический ток, протекающий в какой-либо проводящей среде, принято называть током проводимости. Переменный ток проводимости создает вихревое переменное магнитное поле. Силовые линии такого поля являются замкнутыми. Переменный ток в отличие от постоянного проходит через конденсатор, но этот ток не является током проводимости: он называется током смещения. Этот ток представляет собой изменяющееся во времени электрическое поле. Он создает переменное магнитное поле, как и переменный ток проводимости. Плотность тока смещения j = d D / dt, где D – вектор индукции электрического поля. Вектор индукции связан с электрической напряженностью соотношением: D =εε_o E. В пространстве изменяющееся во времени электрическое поле создает переменное вихревое магнитное поле. При этом каждой точке пространства вектор индукции B возникающего магнитного поля лежит в плоскости, перпендикулярной к вектору индукции D электрического поля. Математическое уравнение, выражающее эту закономерность, входит в систему уравнений, называемых уравнениями Максвелла.

При электромагнитной индукции возникает электрическое поле с замкнутыми силовыми линиями (вихревое поле), которое проявляется как ЭДС индукции. В каждой точке пространства изменение во времени вектора индукции магнитного поля создает переменное вихревое электрическое поле. Векторы D возникающего электрического поля лежат в плоскости, перпендикулярной к векторам B. Математическое уравнение, описывающее эту закономерность, тоже входит в систему уравнений Максвелла. Совокупность переменных электрических и магнитных полей, которые неразрывно связаны друг с другом, называют электромагнитным полем. Из уравнений Максвелла следует, что возникшее в какой-либо точке изменение во времени электрического (или магнитного) поля будет перемещаться от одной точки к другой. При этом будут происходить взаимные превращения электрических и магнитных полей.

Электромагнитные волны представляют собой процесс одновременного распространения в пространстве изменяющихся электрического и магнитного полей. Векторы напряженности электрического и магнитного полей (Е и Н) в электромагнитной волне перпендикулярны друг другу. Вектор v скорости распространения перпендикулярен к плоскости, в которой лежат оба вектора Е и Н. Это справедливо при распространении электромагнитных волн в неограниченном пространстве. В вакууме скорость распространения электромагнитных волн не зависит от длины волны и равна

с = (2,997925 ± 0,000003)·10⁸ м/с.

Скорость электромагнитных волн в различных средах меньше скорости в вакууме              v = c / n,

где n – абсолютный показатель преломления среды. Можно также показать, что       v = c /(εμ)^1/2= c / n.

Совпадение полученных формул с соответствующим соотношением в оптике, позволило Максвеллу сделать заключение: световые волны – это электромагнитные волны.

Энергия электромагнитной волны складывается из энергий переменных электрического и магнитного полей. При этом объемная плотность w энергии электромагнитной волны равна

w =(1/2)(ε_oε) E ²+(μ_oμ) H ²=(ε_oμ_oεμ)^1/2 E · H = E · H / v.

Вектор S = w · v = [ E H ] определяет направление плотности потока электромагнитной энергии и называется вектором Умова – Пойнтинга (или вектором Пойнтинга).

Интенсивностью электромагнитной волны называется величина I, численно равная энергии, которую переносит волна за единицу времени через единицу поверхности, перепендикулярной направлению распространения волны. Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за промежуток времени, равный периоду Т полного колебания:

 .

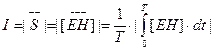При этом предполагается, что Т<<1с, то есть частота электромагнитной волны много больше 1 Гц. Для линейно поляризованной плоской монохроматической волны 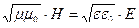, поэтому, вследствие равенства 1/2 среднего значения гармонической функции, выражение для интенсивности имеет вид:

 .

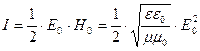Интенсивность плоской монохроматической электромагнитной волны пропорциональна квадрату амплитуды ее электрического вектора.

Спектр электромагнитных волн широк, и условно его можно представить в виде шкалы электромагнитных волн.

Радиоволны – это электромагнитные волны с частотами в диапазоне (10⁵ ÷ 10¹¹) Гц.

Световые волны (инфракрасные, видимые, ультрафиолетовые) – это электромагнитные волны с частотами в диапазоне (10¹¹ ÷ 10¹⁷) Гц.

Рентгеновское излучение – это электромагнитные волны с частотами в диапазоне (10¹⁷ ÷ 10¹⁹) Гц.

Гамма - излучение – это электромагнитные волны с частотами в диапазоне свыше 10¹⁹ Гц.

Электромагнитные волны находят широкое применение в науке и технике, в частности, в радиосвязи, телевидении, радиолокации и радиоастрономии.

ВОПРОСЫ ДЛЯ КОНТРОЛЯ ЗНАНИЙ

1. Магнитное поле. Силовые линии. Вектор магнитной индукции.

2. Принцип суперпозиции магнитных полей.

3. Каково содержание закона Био – Савара – Лапласа?

4. Закон Ампера. Сила Лоренца, ее особенности.

5. Магнитное взаимодействие прямых параллельных токов.

6. Характер движения частиц в магнитном поле.

7. Магнитный поток. Работа при перемещении контура с током в магнитном поле.

8. Как связаны между собой характеристики вещества: магнитная восприимчивость и магнитная проницаемость?

9. Какие вещества называются: парамагнетиками, диамагнетиками? Как они ведут себя во внешнем магнитном поле?

10. Характерные особенности ферромагнетиков. Каковы современные представления о ферромагнетизме?

11. Явление электромагнитной индукции. Правило Ленца.

12. Самоиндукция. ЭДС самоиндукции.

13. Индуктивность и ее единицы измерения.

14. Свободные электрические колебания в колебательном контуре.

15. Ток смещения, плотностью тока смещения.

16. Физический смысл уравнений Максвелла.

17. Плотность энергии электромагнитного поля. Вектор плотности потока электромагнитной энергии (вектор Умова – Пойнтинга).

 

ВОЛНОВАЯ ОПТИКА

Волновая оптика рассматривает явления, в которых проявляется волновая природа света (интерференция, дифракция, поляризация и дисперсия света). Свет – это электромагнитные волны, в которых во взаимно перпендикулярных плоскостях совершают колебания векторы электрической E и магнитной напряженности H. Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие свойства света обусловлены электрической составляющей. Поэтому в дальнейшем, говоря о световом векторе, будем подразумевать под ним вектор напряженности электрического поля E.

Интерференция света

 

При одновременном распространении двух или более волн, колебания в тех точках пространства, куда эти волны одновременно приходят, вызываются каждой из пришедших волн. Результирующее колебание можно рассматривать как сумму составляющих. Для электромагнитных волн речь идет о сложении векторов электрической напряженности Е и магнитной напряженности Н. Явление интерференции света состоит в усилении или ослаблении колебаний, которое происходит в результате сложения двух или более волн, распространяющихся в пространстве, и зависит от соотношения между фазами складывающихся колебаний. Необходимым условием интерференции волн является их когерентность, то есть равенство частот и постоянная во времени разность фаз. Этому условию удовлетворяют только монохроматические световые волны, то есть волны одного цвета. Для световых волн, как и для любых других, справедлив принцип суперпозиции. Результирующий световой вектор двух волн, проходящих через одну точку, равен векторной сумме световых векторов каждой из волн в отдельности. Под световым вектором понимается вектор электрической напряженности. Амплитуда результирующего колебания находится путем геометрического сложения амплитуд исходных колебаний. Условия усиления или ослабления результирующего колебания обычно формулируются не через разность фаз Δφ, а через разность хода волн δ. Известно, что разности фаз Δφ = π, соответствует пройденный волновой путь, равный половине длины волны λ/2. Отсюда можно сформулировать условие максимумов. Максимальное усиление результирующего колебания наступает при разности хода световых волн кратном четному числу полуволн, или целому числу длин волн

δ = 2 k (λ/2) = k λ.

Аналогично формулируется условие минимумов. Наибольшее ослабление результирующего колебания соответствует разности хода, кратной нечетному числу полуволн

δ = (2 k +1)(λ/2),

где k = 0,1,2… называется порядком интерференционного максимума или минимума. Решение задач на интерференцию света необходимо сопровождать рисунком, на котором указываются интерферирующие лучи. При этом различают геометрический и оптический пути света. Когда свет распространяется в среде с абсолютным показателем преломления n, его оптическая длина пути S связана с геометрической длиной l соотношением:         

S = n · l.

При отражении луча от среды оптически более плотной, чем та среда, в которой распространяется падающий луч, фаза колебаний изменяется на π радиан. Говорят, что в данной точке происходит “потеря” половины длины волны. Среди наиболее распространенных примеров интерференции света в природе можно назвать интерференцию в тонких пленках, какими являются мыльные пузыри, радужные пленки нефти на воде, оксидные пленки на поверхности металлов.

Интерференция света – это явление, обусловленное волновыми свойствами. В результате интерференции из-за наложения когерентных волн в одних точках пространства возникают максимумы, а в других – минимумы интенсивности колебаний. При рассмотрении световых колебаний, в данном случае речь идет о перераспределении энергии в пространстве. Световыми принято называть электромагнитные волны, длина которых в вакууме лежит в пределах от 380 до 770 нм. Более короткие и более длинные волны не вызывают в зрительном органе человека световых ощущений. Световые волны называют когерентными, если их разность фаз в интересующей нас точке пространства остается постоянной по времени. Условие максимума интенсивности света заключается в кратности оптической разности хода волн от когерентных источников четному числу 2k полуволн λ/2 или целому числу k длин волн λ

Δ = 2 k ·λ/2,

где Δ = r ₂ – r ₁ – оптическая разность хода волн от когерентных источников до рассматриваемой точки пространства; k = 0, 1, 2, 3,… – целые числа. Условие минимума интенсивности света заключается в кратности оптической разности хода волн нечетному числу (2 k +1) полуволн λ/2:

Δ = (2 k +1)·λ/2.

Если расстояние между двумя когерентными источниками света обозначить через d, расстояние от источников до параллельного им экрана, на котором наблюдается интерференционная картина, обозначить через L, тогда для света с длиной волны λ расстояние между светлыми интерференционными полосами Δ y на экране может быть найдена по формуле

Δ y = λ L / d.

Здесь полагаем, что L >> d.

    При интерференции света в тонких плоскопараллельных пластинках в отраженном свете условия максимума и минимума интенсивности света имеют вид:

условие максимума – Δ = (2 d · n · cos β) – λ/2 = 2 k · λ/2;

условие минимума – Δ = (2 d · n · cos β) – λ/2 = (2 k +1) · λ/2.

Здесь d – толщина пластинки, n – показатель преломления ее материала, β – угол преломления света в пластинке. Для тонких пленок и плоскопараллельных пластин при нормальном падении светового пучка на их поверхность формулы упрощаются (можно считать cos β=1):

условие максимума – Δ = 2 d · n – λ/2 = 2 k · λ/2;

условие минимума – Δ = 2 d · n – λ/2 = (2 k +1) · λ/2.

При интерференции в проходящем свете условия максимума и минимума меняются местами. Поэтому в приводимых ниже формулах условия максимума и минимума для наблюдения в отраженном свете соответствуют условиям минимума и максимума в проходящем. Эти условия, воспользовавшись законом преломления света, можно выразить и через угол падения α. Тогда, при наблюдении в отраженном свете, приведенные выше формулы имеют вид:

условие максимума – Δ = 2 d ·(n ² – sin ²α)^1/2 – λ/2 = 2 k · λ/2;

условие минимума – Δ = 2 d ·(n ² – sin ²α)^1/2 – λ/2 = (2 k +1) · λ/2.

Реально, в отраженном свете интерференция света проявляется в том, что тонкая плоскопараллельная пластинка при освещении ее белым светом выглядит окрашенной в те цвета, для которых выполняется условие максимума. Если толщина пластинки не постоянна, но показатель преломления и угол падения лучей везде одинаковы, в монохроматическом свете можно наблюдать так называемые полосы равной толщины. Это означает, что вдоль какой-либо темной или светлой интерференционной полосы, возникающей на поверхности пластинки, толщина этой пластинки одна и та же. Например, интерференционными полосами равной толщины являются полосы, образующиеся на поверхности прозрачного клина параллельно его ребру (рис. 25, a). Темные полосы видны на тех участках, для которых при наблюдении в отраженном свете разность хода интерферирующих световых волн кратна нечетному числу полуволн. Для k -й по счету темной полосы имеем

Δ = 2 d _k·(n ² – sin ²α)^1/2 – λ/2 = (2 k +1) · λ/2,

где d _k – толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру k. Для k - й по счету светлой полосы будет

Δ = 2 d _k·(n ² – sin ²α)^1/2 – λ/2 = 2 k · λ/2 = k λ.

Здесь все обозначения аналогичны приведенным выше, но соответствуют светлым полосам. Для света, падающего нормально к поверхности, выражение для разности хода упрощается

Δ=2 d _k· n – λ/2 = (2 k +1) · λ/2, т.о. 2 d _k· n = k λ + λ.

Если последнее условие записать для двух соседних полос и вычесть из одного из них другое, получим:

2 n (d _k+1 – d _k) = λ.

 

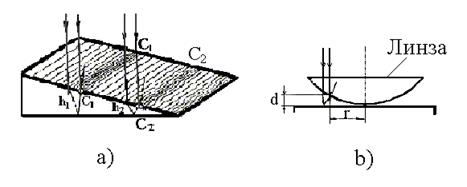
Рис. 25. Схемы наблюдения интерференции:

а– полосы равной толщины; b – кольца Ньютона

 

Обозначим через Х расстояние между темными или светлыми интерференционными полосами. Теперь можно утверждать, что малый угол γ при вершине клина, измеренный в радианах, равен

γ = (d _k+1 – d _k)/ Х.

Угол γ очень мал, поэтому полагаем sinγ ≈ γ. Число приходящихся на единицу длины темных или светлых интерференционных полос вдоль направления, перпендикулярного ребру клина, равно

N / l = 1/ Х = 1/(d _k+1 – d _k) = 2γ· n /λ.

Полосы равного наклона между плосковыпуклой линзой и пластинкой при параллельности плоской поверхности линзы и пластинки имеют вид колец. Пучок света при этом направлен вдоль главной оптической оси линзы. Подобное устройство называют установкой для наблюдения колец Ньютона (рис.25 b). Результат интерференции зависит от оптической разности хода, которая в случае нормального падения лучей имеет вид

Δ = 2 d _k n.

В записанном соотношении d _k – толщина клина из вещества, заполняющего пространство между линзой и пластинкой в месте, где наблюдается интерференция (k -е светлое или темное кольцо), n – абсолютный показатель преломления этого вещества. Для воздуха n = 1. Толщина клина в месте наблюдения k -го светлого или темного кольца, может быть найдена из геометрических соображений как d _k= r _k²/2 R, R – радиус кривизны линзы. При наблюдении в проходящем свете условие максимума интерференции (светлое кольцо) соответствует разности хода лучей Δ, кратной четному числу полуволн:

Δ = 2 d _k n = 2 k ·λ/2 = k ·λ.

Условие минимума (темное кольцо), соответствующее кратности Δ нечетному числу полуволн, в проходящем свете оно имеет вид

Δ = 2 d _k n = (2 k +1)λ/2.

Здесь k = 0, 1, 2, 3,… При наблюдении в отраженном свете условия максимума и минимума меняются местами. Центральное светлое пятно в проходящем свете и центральное темное в отраженном свете считаем нулевыми кольцами (k = 0). В проходящем свете радиусы светлых колец Ньютона находятся по формуле

r _k = (2 d _k R)^1/2= (k·R· λ)^1/2,

k = 1, 2, 3,… Радиусы темных колец находятся по формуле

r _k = [(2 k – 1)· R ·λ]^1/2.

В опыте с кольцами Ньютона возможно определение показателя преломления вещества, заполняющего пространство между линзой и пластинкой. По наблюдениям в проходящем свете можно найти

n = k ·λ· R / r _k²,

где r_k – радиус k -о светлого кольца. Если наблюдается темное кольцо с радиусом r _k, то

n = (2 k – 1)λ· R / r _k².

Наблюдения можно проводить и в отраженном свете. Но формулы для светлого и темного колец нужно поменять местами.

    При решении некоторых задач, в которых рассматривается установка для получения колец Ньютона, можно использовать формулу для тонкой плосковыпуклой линзы

(n – 1)/ R =1/ F = D.

Здесь R – радиус кривизны выпуклой поверхности линзы, F – фокусное расстояние, D – оптическая сила линзы, n – относительный показатель материала линзы.

"Просветление" оптики связано с нанесением на поверхность линз тонких пленок. Чтобы оценить необходимую толщину пленки для максимального ослабления отражения света с длиной волны λ., рассмотрим малый участок пленки, нанесенной на поверхность стекла (рис. 26). Абсолютные показатели преломления соответственно равны: воздуха n = 1, стекла n ₁, пленки n ₂. Причем n ₁> n ₂> n. Из световой волны выделим узкий луч SA. В точках А и В падающий луч частично отражается и частично преломляется. Отраженные лучи AS ₁ и CS ₂ могут интерферировать между собой. Поскольку показатель преломления воздуха меньше показателя преломления пленки, который, в свою очередь, меньше показателя преломления стекла, в обоих случаях происходит отражение от оптически более плотных сред. В результате изменение фазы колебаний, связанное с отражением от границ раздела сред, оказывается одинаковым для обоих интерферирующих лучей. В этом случае условие интерференции для максимального ослабления отраженного света имеет вид Δ = (2 k +1)λ/2.

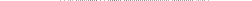 Рис. 26. Интерференция света в тонких пленках

 

Из схемы, представленной на рис. 26, следует, что оптическая разность хода Δ определяется соотношением Δ = l ₂n₂ – l ₁ n. Здесь l ₂ = АВ + ВС, а l ₁ = AD. Если угол падения α мал (свет падает почти нормально к поверхности пленки), то АВ + ВС = 2 d, здесь d – толщина пленки. Тогда Δ = 2 d · n ₂ = (2 k +1)λ/2. Необходимая толщина пленки может быть найдена из соотношения

d = (2 k +1)λ/4 n ₂.

Минимальная толщина пленки d _min соответствует k = 0; d _min= λ/4 n ₂. Полученный результат означает, что свет с длиной волны λ будет полностью "гаситься" на просветляющей пленке с оптической толщиной d _опт = n ₂· d _min = n ₂λ/4. Для света с длиной волны λ', отличной от λ, полного гашения наблюдаться не будет. Это связано с тем, что кроме разности хода λ'/2 у интерферирующих волн возникает дополнительная оптическая разность хода Δλ/4 = (λ – λ')/4, которая соответствует разности фаз суммируемых световых колебаний Δφ=π[1+(λ – λ')/2λ']. Считая интенсивность I интерферирующих волн одинаковой, найдем относительную интенсивность I _s/ I суммарных колебаний через отношение квадратов соответствующих амплитуд. Амплитуду суммарных колебаний определим, воспользовавшись теоремой косинусов. В результате получаем

 

(I _s/ I) = 2 + 2 cos (Δφ) = 2 + 2 cos {π [1 + (λ – λ')/2λ']}.

 

    Явление интерференции света используется в ряде точных измерительных приборов, называемых интерферометрами. На рис. 27 a изображена принципиальная схема интерферометра Жамена, применяемого для точных измерений показателей преломления газов. Две одинаковые толстые плоскопараллельные стеклянные пластины, обозначенные на рис. 27 а как А и В, установлены параллельно друг другу. Световой луч от монохроматического источника S падает на пластину под углом α, равным 45^о. В результате его отражения из пластины выходят два когерентных луча. Пройдя через одинаковые кюветы, лучи после отражения второй пластиной собираются линзой Л и интерферируют. Если одна из кювет заполнена газом с известным абсолютным показателем преломления, а другая – с измеряемым, оптическую разность хода между интерферирующими лучами можно найти как               

Δ = (n ₂ – n ₁) l.

 

Следовательно, n ₂= n ₁+ k ·λ/ l, где k – порядок интерференционного максимума. Изменение оптической разности хода на длину волны λ вызывает смещение интерференционной картины на одну полосу, а изменение на k ·λ – смещение на k полос. Упрощенная схема интерферометра Майкельсона приведена на рис. 27 b. Вертикальный луч монохроматического света от источника S падает под углом 45^о на плоскопараллельную полупрозрачную пластинку. Часть света проходит через нее к зеркалу З₂, другая часть отражается и идет к зеркалу З₁.

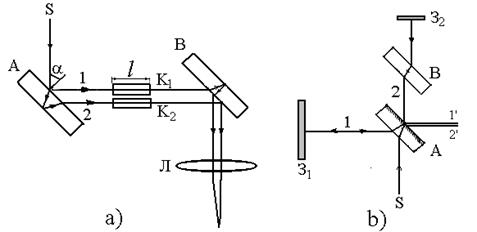
Рис. 27. Интерферометры: а – Жамена; b –Майкельсона

 

Отразившиеся от зеркал лучи 1' и 2' когерентны. Результат их интерференции зависит от оптической разности хода. Смещение одного из зеркал или изменение оптической длины одного из плеч интерферометра на половину длины волны λ/2 приводит к смещению интерференционной картины на одну полосу, а изменение на k ·λ/2 – смещение на k полос. Интерферометр Майкельсона также используется для точных измерений показателей преломления различных веществ.   

Дифракция света

Дифракцией называют процессы, связанные с отклонением волн от прямолинейного распространения на границах непрозрачных для них препятствий. Эти процессы сопровождаются интерференционным перераспределением энергии. Огибая препятствие, волна заходит в область геометрической тени. Дифракция света сопровождается интерференцией дифрагировавших лучей. Дифракция возникает в том случае, когда фронт волны не является безграничным, а частично экранирован. Например, вблизи границ непрозрачных или прозрачных тел, сквозь малые отверстия. Интенсивность при дифракционных явлениях можно приближенно рассчитать, пользуясь принципом Гюйгенса – Френеля. Согласно этому принципу все точки волновой поверхности являются центрами воображаемых когерентных источников, которые излучают сферические волны. Эти волны называют элементарными. Огибающая элементарных волн представляет собой волновую поверхность для последующего момента времени. Она возникает в результате интерференции элементарных волн. При этом предполагается, что огибающая перемещается лишь в одну сторону от волновой поверхности (по направлению распространения волны).  Принцип Гюйгенса – Френеля позволяет рассмотреть многие случаи дифракции света и дает результаты, удовлетворительно согласующиеся с опытом. Чтобы понять суть метода, разработанного Френелем, определим амплитуду светового колебания, возбуждаемого в точке Р сферической волной, приходящей от точечного источника S, рис. 28. Разобьем изображенную на рисунке волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки Р отличаются на λ/2. Это зоны Френеля. Колебания, приходящие в точку Р от аналогичных точек двух соседних зон, находятся в противофазе, поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на π. При небольшом числе k зон Френеля площади их примерно одинаковы. В этом случае радиус k -й зоны Френеля можно определить из соотношения

r _k=[ a · b · k ·λ/(a + b)]^1/2.

 

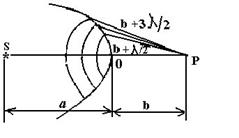
Рис. 28. Схема зон Френеля

 

Расстояние от зоны до точки Р с ростом номера зоны k увеличивается медленно, поэтому амплитуда А _k колебания, возбуждаемого k -й зоной в точке Р, убывает монотонно. Приближенно можно считать, что

A _k=(A _k-1+ A _k+1)/2 и A = A ₁/2.

То есть амплитуда в точке Р равна половине амплитуды центральной зоны. Если на пути волны поставить непрозрачный экран с отверстием, открывающим только центральную зону, тогда амплитуда в точке Р будет равна А, а интенсивность света будет в четыре раза больше, чем при отсутствии преград между точками S и Р. Если же отверстие таково, что открывает две зоны Френеля, то амплитуды от этих зон (примерно одинаковые) придут в точку Р в противофазе, и в ней будет наблюдаться минимум интенсивности света. Из сказанного следует: если в открытый фронт волны входит четное число зон Френеля, то наблюдается минимум интенсивности света; если k – нечетное, то наблюдается в точке Р максимум интенсивности света.

Различают два случая дифракции света: дифракцию Френеля, или дифракцию в сходящихся лучах, и дифракцию Фраунгофера, или дифракцию в параллельных лучах. В первом случае на препятствие падает сферическая или плоская волна, а дифракционная картина наблюдается на экране, находящемся за препятствием на конечном расстоянии от него. Фактически, этот случай мы уже рассмотрели. Во втором случае на препятствие падает плоская волна, а дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути прошедшего через препятствие света. Рассмотрим дифракцию Фраунгофера на щели. Схема опыта представлена на рис. 29. Пусть параллельный пучок монохроматического света падает нормально на непрозрачный экран, в котором прорезана узкая щель шириной а. В соответствии с принципом Гюйгенса – Френеля все точки щели являются когерентными источниками света, колеблющимися в одной фазе. Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении φ, равна δ = a · sin φ. Разобьем щель MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Все зоны в заданном направлении излучают свет совершенно одинаково. При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но с противоположными фазами.

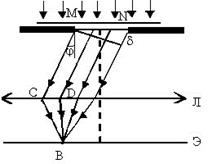
Рис. 29. Дифракция света на щели

 

Результат интерференции в точке В определяется тем, сколько зон Френеля укладывается в щели. Если число зон четное, то

a · sin φ = ±2 k (λ/2) (k = 1,2…)

и наблюдается дифракционный минимум. Если число зон нечетное, то

a · sin φ = ±(2 k + 1)(λ/2)

и наблюдается дифракционный максимум. Величина k называется порядком дифракционного максимума (или минимума).

Совокупность большого числа узких параллельных щелей, имеющих одинаковую ширину и расположенных в плоскости на одинаковом расстоянии друг от друга, называется плоской дифракционной решеткой. Расстояние, равное сумме ширины одной щели и ширины промежутка между соседними щелями, называется постоянной (или периодом) дифракционной решетки. Дифракционную картину можно наблюдать либо с помощью зрительной трубы, либо на экране, расположенном за дифракционной решеткой. При нормальном падении лучей на поверхность дифракционной решетки направления, в которых будет наблюдаться максимальная освещенность на экране, определяются из условия:

d · sin φ = ± k λ (k = 0,1,2…),

где d – период дифракционной решетки, φ – это угол между нормалью к дифракционной решетке и направлением на соответствующий дифракционный максимум. Как следует из формулы, если на решетку падает белый свет, то для более коротких волн условие максимума выполняется при меньших углах. Направления, в которых интенсивность освещения будет минимальна, определяются из условия:

а · sin φ = ± k λ (k = 1,2, 3…),

где а – ширина щели дифракционной решетки. Разрешающая способность R дифракционной решетки, то есть способность ее представить раздельно две спектральные линии, определяется по формуле R = kN, где N – общее число штрихов дифракционной решетки, k – порядок дифракционного максимума.

    Когда на дифракционную решетку падает не монохроматический, а белый свет, дифракционные максимумы, соответствующие разным длинам волн, будут расположены в различных частях экрана. Возникает дифракционный спектр. При k = 1, 2, 3, …. возникают спектры первого, второго, третьего и так далее порядков. Дифракционный спектр называют нормальным, поскольку протяженность световых зон соответствует диапазонам их длин волн. Чего не наблюдается, например, в дисперсионном спектре, образуемом при разложении белого спектра призмой. Там красная область оказывается растянутой по сравнению с синей и фиолетовой. Дифракционная решетка сильнее отклоняет более длинные красные волны, чем синие и фиолетовые. При нормальной дисперсии в призме картина будет противоположная: отклонение красных лучей будет наименьшим.

    С явлением дифракции непосредственно связана разрешающая способность оптических приборов. В любом оптическом приборе (в том числе и в глазу) на краях диафрагм, оправ и т.п. происходит дифракция света. В результате этого точки предметов отображаются в виде маленьких кружочков, соседние из которых сливаются, и их невозможно отличить. Каждый прибор характеризуется максимальной разрешающей способностью (предельным разрешением). Предельное разрешение определяется или минимальным углом, под которым различимы две соседние точки предмета, или минимальным расстоянием между точками, при котором они различимы. Для глаза или подзорной трубы предельное разрешение (минимальный угол зрения) δ определяется формулой

δ = 0,61·λ/ r.

Для микроскопа предельное разрешение (

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: