Молекулярная физика и термодинамика

 

Молекулярная физика изучает физические свойства и агрегатные состояния тел в зависимости от их молекулярного строения, сил взаимодействия между частицами тела и характера движения этих частиц. В ее основе лежат основные положения молекулярно-кинетической теории строения вещества: а) все тела состоят из атомов и молекул; б) атомы и молекулы находятся в состоянии непрерывного хаотического движения; в) между частицами тела действуют силы притяжения и отталкивания.

Термодинамика, подобно геометрии и механике, аксиоматическая наука. В ее основе лежат принципы, являющиеся обобщением всей совокупности экспериментальных данных о превращении теплоты в механическую работу. То обстоятельство, что теплота представляет собой одну из форм энергии, которая может превращаться в другие формы, было установлено лишь в девятнадцатом веке. Термодинамика изучает в основном общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Поскольку тела состоят из очень большого количества молекул (например, при нормальных условиях в 1 см³ воздуха содержится около 3·10¹⁹ молекул), то простое применение механических методов к описанию поведения этих тел ведет к непреодолимым трудностям. Поэтому при изучении физических свойств тел, состоящих из большого числа частиц, используются два взаимно дополняющих друг друга метода – статистический и термодинамический. Статистический метод базируется на анализе свойств макроскопических систем с помощью методов математической статистики. Термодинамический метод состоит в изучении свойств системы путем анализа условий, при которых в системе происходит превращение энергии, и установлении связей между макроскопическими свойствами вещества. Термодинамической системой называется совокупность макроскопических тел, обменивающихся энергией друг с другом и с внешней средой (другими телами). Состояние термодинамической системы можно описать с помощью термодинамических параметров: температуры, давления и молярного объема. Температура – это физическая величина, характеризующая энергию хаотического молекулярного движения и состояние термодинамического равновесия макроскопической системы. В системе единиц СИ используются термодинамическая температура Т (иначе называемая абсолютной температурой), измеряемая в Кельвинах. Давление р – физическая величина, численно равная силе, действующей нормально на единицу поверхности. В системе СИ давление измеряется в Н/м = Па (паскаль). Объем, занимаемый 1 молем вещества, называют молярным. Измеряется в м³/моль.          

 

 2.1. Элементы молекулярно-кинетической теории     

 

    Все материальные тела условно можно разделить на твердые, жидкие и газообразные. В качестве критерия такого разделения используется величина ε(Т, р), равная отношению средней потенциальной энергии взаимодействия к средней кинетической энергии молекул (атомов) тела. Для твердых тел ε >> 1; жидких ε ≈ 1 и газообразных ε << 1. Для описания физических свойств реальных тел и процессов используются модельные представления. В молекулярно- кинетической теории газов используется модель идеального газа. В этой модели частицы газа рассматриваются как материальные точки, а потенциальная энергия их взаимодействия не учитывается. Частицы газа движутся хаотически. Их столкновения между собой и со стенками сосуда считаются абсолютно упругими. Для любого газа, к которому применимы такие допущения, справедливы следующие законы, называемые законами идеальных газов:        

    1) закон Бойля–Мариотта: при постоянной температуре для данной массы газа произведение давления газа на его объем есть величина постоянная p · V = const;

    2) первый закон Гей-Люссака: при постоянном давлении для данной массы газа объем газа изменяется линейно с температурой

V = V _о(1+α t),

где V _о – объем газа при температуре t = 0С и α=1/273 К^-1;  

    3) второй закон Гей-Люссака: при постоянном объеме для данной массы газа давление газа изменяется линейно с температурой

p = p _о(1+α t),

где р о – давление газа при температуре t = 0С и α =1/273 К^-1; этот закон часто называют законом Шарля. Законы Гей-Люссака можно записать для шкалы Кельвина в виде

V = α· V _o· T и р = α· р _o· Т;

4) закон Авогадро: при одинаковых давлениях и одинаковых температурах в равных объемах различных идеальных газов содержится одинаковое число молекул; в одном моле различных веществ содержится N_А = 6,02·10²³ молекул – это постоянная (или число) Авогадро;       

    5) закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений р_i, входящих в нее газов

р = ∑ p _i = р ₁ + р ₂ +... р _n ;

р_i – это давление, которое оказывал бы определенный газ из смеси, если бы он один занимал весь объем при той же температуре.         

Равновесное давление в однородной термодинамической системе является функцией ее объема и температуры p = f (V, T). Уравнение р = р (V, Т) называется уравнением состояния системы. Для идеального газа – это уравнение Клапейрона – Менделеева:

p · V = (m /μ)· R · T,

где m – масса газа, μ – молярная масса, R – универсальная газовая постоянная; R = 8,31 Дж/(моль·К). Уравнение состояния идеального газа можно переписать в виде:

p = n · k · T или p · V = N · k · T;

здесь n – число молекул в единице объема газа, N – число молекул газа, k = R / N_А = 1,3810^-23(Дж/К) – постоянная Больцмана. Для идеального газа пренебрегают потенциальной энергией взаимодействия его частиц, считается, что частицы одноатомного газа обладают только кинетической энергией поступательного движения Е _кi=(1/2) m _i v _i². Таким образом, внутренняя энергия газа U, состоящего из N одинаковых частиц, будет в N раз больше кинетической энергии одной частицы с массой m _i и средней скоростью v _i, которую принято называть среднеквадратичной. Предполагая, что молекулы газа движутся хаотически, и число взаимных столкновений между ними значительно меньше числа столкновений со стенками сосуда, можно получить уравнение, связывающее давление р, объем V и Е _к. Это уравнение называется основным уравнением молекулярно-кинетической теории идеальных газов, оно имеет вид

p · V =(2/3)· E _к.

Из сказанного следует вывод, что давление газа возникает в результате столкновений молекул газа со стенками сосуда. Вводя в рассмотрение среднюю квадратичную скорость поступательного движения молекул газа, можно для однородного идеального газа записать выражение для средней кинетической энергии поступательного движения одной частицы газа:

ε_ср.= (3/2)· kT.

Последняя формула показывает, что термодинамическая температура Т является величиной, пропорциональной средней кинетической энергии поступательного движения одной частицы идеального газа.  

введем понятие степени свободы системы. Степенью свободы механической системы называется число независимых координат, определяющих ее положение и конфигурацию в пространстве. Число степеней свободы принято обозначать латинской буквой i. Частицы одноатомного газа можно считать материальными точками. Чтобы определить положение точки в пространстве, необходимы три независимые координаты (х, у, z). Следовательно, число степеней свободы для частицы одноатомного газа i =3. Для двухатомной молекулы с жесткой связью (в виде гантели) необходимы три координаты для описания поступательного движения (i _п=3) и две координаты для описания вращательного движения вокруг двух взаимно перпендикулярных осей, не проходящих через оба атома (i _вр=2). Таким образом, общее число степеней свободы будет равно пяти, поскольку i = i _п+ i _вр= 5. Для трехатомной молекулы с жесткими связями между атомами необходимы три поступательных (i _п = 3) и три вращательных (i _вр = 3) степени свободы. Общее число степеней свободы трехатомной или многоатомной молекулы идеального газа равно шести, поскольку i = i _п + i _вр = 6. Доказывается, что все степени свободы энергетически равноправны. Сущность этого положения выражает закон о равномерном распределении энергии по степеням свободы молекул: если система молекул находится в термодинамическом равновесии при температуре Т, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы. На каждую поступательную и вращательную степени свободы приходится энергия, равная (1/2)kТ. Таким образом, среднюю кинетическую энергия одной молекулы можно подсчитать из соотношения

ε_ср= (i /2)· k · T, i = i _п+ i _вр .

Внутренняя энергия идеального газа находится как суммарная кинетическая энергия его частиц. Для газа, содержащего молей, справедливо соотношение

U = (i /2)·(m /μ)· R · T.

Здесь число молей ν = m /μ определяется отношением массы газа к его молярной массе. Универсальная газовая постоянная R равна произведению двух констант: постоянной Больцмана и числа Авогадро.

2.2. Элементы термодинамики  

 

Термодинамика изучает превращения энергии в различных процессах, сопровождающихся тепловыми эффектами. Передача энергии от одного тела к другому осуществляется путем совершения работы А или путем теплового обмена (передачи теплоты Q). Работа есть мера переданной от одного тела к другому механической энергии. Работа, совершенная телом (системой), считается положительной   (А > 0), а работа, совершенная над телом (системой), – отрицательной (А < 0). Теплота Q – это мера переданной от одного тела к другому энергии теплового движения молекул посредством теплообмена между телами. Теплота, полученная телом (системой), считается положительной (Q > 0), а отданная телом (системой), – отрицательной (Q < 0). Применение закона сохранения и превращения энергии к тепловым процессам приводит к уравнению

Δ Q = Δ U + A.

Это уравнение представляет собой математическую запись первого начала термодинамики: для системы, находящейся в состоянии термодинамического равновесия, количество теплоты Δ Q, сообщенное системе, расходуется на изменение ее внутренней энергии Δ U и на совершение системой работы А против внешних сил. Если система периодически возвращается в первоначальное (исходное) состояние, то изменение внутренней энергии Δ U = 0. Следовательно, в таком процессе совершенная системой работа А = Δ Q. Последнее равенство говорит о том, что невозможно построить периодически действующий двигатель, который бы совершал работу, большую подводимой к нему извне энергии. То же самое можно сказать иначе: вечный двигатель первого рода невозможен. Для элементарного изменения состояния системы уравнение первого начала имеет вид                  

δ Q = dU + δ A.

В такой форме записи подчеркивается, что внутренняя энергия является полным дифференциалом (dU), а работа и теплота (δ A и δ Q) не являются полными дифференциалами. Сказанное означает, что внутренняя энергия – это функция состояния системы, а работа и теплота – функции процесса.         

    Примечание. Функцией состояния называется такая физическая характеристика системы, изменение которой при переходе системы из одного состояния в другое не зависит от вида термодинамического процесса, а определяется значениями параметров начального и конечного состояний.

Во время протекания термодинамического процесса система может совершать положительную или отрицательную внешнюю работу. Другими словами, система совершает работу над средой или среда над системой. В качестве примера рассмотрим расширение газа в цилиндре с поршнем. Пусть давление газа есть р, а площадь поршня – S; тогда сила, действующая на поршень, равна р · S. При перемещении поршня на бесконечно малое расстояние dl совершается работа δА = р · S · dl. Поскольку произведение S · dl равно увеличению объема системы dV, можно записать:

δА = р · d V,

если давление однородно по всему объему, находящемуся под поршнем. Выражение справедливо и в общем случае, оно не зависит от формы сосуда. Для конечного процесса полная работа, проделанная системой в результате равновесного расширения от объема V ₁ к объему V ₂, может быть найдена в результате интегрирования:

.

При использовании графического метода работа А получает простое геометрическое истолкование. На диаграмме давление – объем (р – V) процесс перехода системы из состояния 1 в состояние 2 изображается кривой, соединяющей точки 1 и 2 (рис. 16). Форма этой кривой зависит от вида рассматриваемого процесса. Работа графически соответствует заштрихованной площади, ограниченной кривой p = f (V) осью абсцисс и вертикальными прямыми, соответствующими начальному и конечному объему.

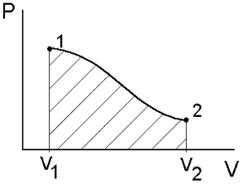
Рис. 16. Диаграмма давление – объем

 

Особенно важны процессы, в которых начальное и конечное состояние системы одинаковы. Такие процессы называются циклическими или циклами (рис. 17).

Рис. 17. Диаграмма циклического процесса

 

На диаграмме давление – объем цикл изображается кривой 13241. Работа А, выполненная системой во время цикла, равна площади, заключенной внутри этой кривой. В самом деле, работа, выполняемая во время процесса 132, положительна и равна площади, заштрихованной один раз. Работа, выполняемая во время процесса 241, отрицательна и равна площади, заштрихованной дважды. Суммарная работа равна разности этих двух площадей и, следовательно, равна площади внутри замкнутой кривой, изображающей цикл. Заметим, что работа положительна, если цикл протекает по часовой стрелке, и отрицательна в противном случае. Когда объем системы во время процесса не изменяется, то есть V = const и dV = 0, работа не совершается: δА = 0.

Изопроцессами принятоназывать термодинамические процессы, протекающие при неизменном значении какого-либо параметра состояния (при неизменной массе системы).

Изохорным называют термодинамический процесс, протекающий при постоянном объеме системы.

Изобарным называют термодинамический процесс, протекающий при постоянном давлении.

Изотермическим называют термодинамический процесс, протекающий при постоянной температуре.

Адиабатическим (или адиабатным) называют процесс, осуществляемый термодинамической системой без теплообмена с окружающей средой.

Применим первое начало термодинамики к изопроцессам, протекающим в идеальных газах.

1. Изохорный процесс (V = const). Газ не совершает работу,   δ А = 0, и вся подводимая к газу теплота идет на увеличение его внутренней энергии:                

δ Q = dU.

2. Изобарный процесс (р = const). Работа газа при таком процессе находится из соотношения:

А = р ·(V ₂ –  V ₁).

Подводимая к газу теплота расходуется на увеличение его внутренней энергии и на совершение газом работы:

Δ Q = δ U + p · dV.

 3. Изотермический процесс (Т = const). Внутренняя энергия газа остается постоянной U = const, а количество теплоты, подведенное к газу, целиком расходуется на совершение работы расширения

A = (m /μ)· R · T · ln (V ₂/ V ₁).

4. Адиабатический (адиабатный) процесс (δ Q = 0) описывается уравнением адиабаты (уравнение Пуaссона)

p · V ^γ = const.

Здесь показатель степени γ = C _р/ C _v. Это отношение теплоемкости при постоянном давлении к теплоемкости постоянном объеме. Для такого процесса δ A = – dU – внешняя работа совершается газом за счет уменьшения его внутренней энергии. Кривая адиабаты в координатах давление – объем идет круче изотермы. Газ при адиабатическом расширении охлаждается, а при сжатии – нагревается.

Теплоемкостью тела С называется отношение элементарного количества теплоты δ Q, сообщенного телу в каком-либо процессе, к соответствующему изменению температуры тела: C = δ Q / dT.

Удельная теплоемкость с _уд – это теплоемкость единицы массы однородного вещества: с _уд = δ Q /(m · dT). Измеряется в Дж/(кг·К).

Молярной теплоемкостью называют теплоемкость одного моля вещества: с_m = δ Q /(ν· dT). Измеряется в Дж/(моль·К).

Принято различать теплоемкости при постоянном объеме    C _v = (δ Q / dT)_v и постоянном давлении C _p = (δ Q / dT)_p. Чтобы оценить теплоемкость идеального газа, воспользуемся первым началом термодинамики и выражением для внутренней энергии газа. Для одного моля идеального газа, находим:

C _v = (i /2) R; C_p = (i +2) R /2; C _p – C _v = R.

Соотношение C _p – C _v = R, записанное для молярных теплоемкостей, называется уравнением Майера. Для одного моля идеального одноатомного газа (i = 3) получаем:

С _v = (3/2) R, C _p = (5/2) R, γ= C _р/ C _v = 1,66.

Для идеального двухатомного газа (i = 5):

С _v = (5/2) R, C _p= (7/2) R, γ= C _р/ C _v = 1,4.

Для идеального трехатомного и многоатомных газов (i = 6):

C _v =3 R,    C _p = 4 R, γ = C _р/ C _v = 1,33.

Важным понятием в термодинамике является обратимость процессов. Обратимым термодинамическим процессом называется процесс, происходящий с системой, когда при возвращении системы в исходное состояние, во всей системе и окружающих систему телах не происходит никаких изменений. Необратимый термодинамический процесс – это такой процесс, при котором возвращение системы в исходное состояние сопровождается изменениями в самой системе или окружающих систему телах. Привести пример реального обратимого процесса не представляется возможным. В качестве примера необратимого процесса можно рассмотреть процесс расширения газа в пустоту: газ, первоначально занимающий часть объема сосуда и отделенный от другой части непроницаемой перегородкой, после удаления перегородки через некоторое время займет весь объем сосуда. Очевидно, что самопроизвольно, без дополнительных затрат энергии, газ уже не соберется в первоначальном объеме. Квазистатическим называется процесс, текущий бесконечно медленно и представляющий собой последовательность равновесных состояний. Такой процесс является обратимым. Обратимые процессы протекают в обоих направлениях (как в прямом направлении, так и в обратном). Необратимые процессы могут протекать только в одном направлении. Первое начало термодинамики не позволяет определить направление протекания термодинамических процессов. Обобщение результатов многочисленных экспериментов привело к выводу о невозможности построения такой тепловой машины (вечного двигателя второго ряда), рабочее тело которой (например, газ), совершая обратимый замкнутый процесс, получило бы энергию в форме теплоты от одного внешнего тела и целиком передало ее в форме работы другому внешнему телу. Сущность этого вывода и составляет основу второго начала термодинамики. Можно привести несколько формулировок второго начала термодинамики. На первый взгляд они не похожи друг на друга, но по физическому смыслу выражают одно и то же:        

    1) не существует вечного двигателя второго рода; 

2) при тепловом контакте двух тел с различными температурами тепло самопроизвольно переходит от более горячего тела к более холодному, а не наоборот;  

3) невозможна тепловая машина периодического действия, у которой коэффициент полезного действия больше, чем у цикла Карно при тех же температурах горячего и холодного тепловых резервуаров (нагревателя и холодильника);

4) энтропия замкнутой системы не может убывать.

Французский инженер Карно рассмотрел идеальный круговой процесс, положенный в основу работы тепловой машины. Круговым процессом (циклом) называется такой процесс, при котором система после ряда изменений возвращается в исходное состояние. Машина Карно представляет собой систему цилиндр – поршень. Рабочим телом в машине является идеальный газ. Машина не имеет клапанов, то есть одно и то же рабочее тело используется многократно. Тепловая машина имеет два тепловых резервуара: горячий с температурой Т ₁ и холодный с температурой Т ₂. Цикл Карно состоит из двух изотермических и двух адиабатических процессов (рис. 18).

Рис. 18. Диаграмма цикла Карно

 

 В процессе изотермического расширения рабочее тело получает от горячего теплового резервуара количество теплоты + Q ₁ (участок АВ); затем происходит процесс адиабатического расширения (участок ВС), при котором рабочее тело охлаждается до температуры Т ₂. После чего происходит изотермическое сжатие (участок CD), в процессе которого рабочее тело отдает холодному тепловому резервуару количество теплоты – Q ₂. Затем имеет место адиабатическое сжатие (участок DA), и температура рабочего тела повышается до Т ₁. Полная работа за цикл А = Q ₁ – Q ₂. Термический коэффициент полезного действия (КПД) цикла карно равен

η = A / Q ₁ = (Q ₁ – Q ₂)/ Q ₁ = (T ₁ – T ₂)/ T ₁.

КПД цикла Карно не зависит от рода рабочего тела, а определяется только температурами нагревателя и холодильника.

Величина Q / Т называется приведенным количеством теплоты. Для цикла карно алгебраическая сумма приведенных теплот равна нулю. доказывается, что она равна нулю и для любого обратимого кругового процесса; это так называемое равенство Клаузиуса. 

    Для характеристики направления теплообмена вводится термодинамическая характеристика S, называемая энтропией системы: dS =δ Q / T. Изменение энтропии в любом обратимом процессе, переводящем систему из состояния 1 в состояние 2, равно

 .

Всякой термодинамической системе присуща некая величина, которая подобно температуре обусловлена неупорядоченностью молекулярных и внутримолекулярных движений. Эта величина носит название энтропии. Ее физический смысл был выяснен Больцманом. Он рассмотрел микросостояния и макросостояния термодинамических систем. Микросостояние системы характеризуется состояниями составляющих ее молекул. При этом молекулы считаются отличающимися друг от друга. Макросостояния системы характеризуются только числом молекул (независимо от их номера), входящих в систему. Вводится понятие термодинамической вероятности состояния W. Это число микросостояний системы, соответствующих данному макросостоянию. Как правило, W >>1. Формула Больцмана, связывающая энтропию с термодинамической вероятностью, имеет следующий вид

S = k · lnW,

где k – постоянная Больцмана. Таким образом, энтропия выступает как количественная мера степени молекулярного беспорядка. Для обратимых процессов изменение энтропии

Δ S = S ₂ – S ₁ = 0 (или S ₁= S ₂).

При необратимых процессах энтропия системы возрастает: Δ S > 0. Для произвольного элементарного термодинамического процесса можно записать: 

dS ≥ δ Q / T.

Знак равенства относится к обратимым процессам, а знак неравенства – к необратимым. Для замкнутой (адиабатической) системы dS ≥ 0. Приведенный результат является математической записью второго начала термодинамики: энтропия изолированной системы при любых происходящих в ней процессах не может убывать и максимальное значение энтропии соответствует состоянию равновесия (наиболее вероятному состоянию системы, для которой число микросостояний максимально). При всех процессах, происходящих в замкнутой системе, система самопроизвольно не может переходить из более вероятного в менее вероятное состояние.  

    Наконец, Нернст сформулировал утверждение: при абсолютном нуле температуры энтропия системы равна нулю:

S → 0 при T → 0.

Это утверждение получило название третьего начала термодинамики.

Есть еще один принцип, устанавливающий существование температуры, как функции состояния системы. Им определяется тепловое равновесие термодинамических систем. Его называют принципом температуры или нулевым началом термодинамики. Если две термодинамические системы находятся в тепловом равновесии и одна из них находится в тепловом равновесии с третьей, то и другая будет находиться с третьей в таком же тепловом равновесии, как если бы между ними существовал тепловой контакт.

Основное уравнение термодинамики для обратимых процессов, объединяющее первое и второе начала термодинамики, имеет вид

T · dS = dU + δ A.

 

2.3. Элементы физической кинетики           

        

    Если в системе существует пространственная неоднородность плотности (массы), температуры или импульса упорядоченного движения молекул газа в разных слоях, то на хаотическое тепловое движение молекул накладывается упорядоченное движение. Такое упорядоченное движение выравнивает неоднородности. Возникающие процессы называются явлениями переноса. Среди явлений переноса принято различать диффузию, теплопроводность и внутреннее трение, которое часто называют вязкостью. При диффузии происходит направленный перенос массы, теплопроводность характеризуется направленным переносом энергии, внутреннее трение (вязкость) – направленным переносом импульса (количества движения). В основе всех явлений переноса лежит один и тот же молекулярный механизм – хаотическое тепловое движение и столкновения молекул газа.

Между двумя последовательными соударениями молекула движется прямолинейно и равномерно, проходя в среднем расстояние <λ>, называемое средней длиной свободного пробега. Можно показать, что

,

здесь d – эффективный диаметр молекулы; n – концентрация молекул. Диффузия – это обусловленное хаотическим движением молекул явление постепенного взаимного проникновения граничащих друг с другом веществ. Эксперименты показывают, что даже в газах диффузия происходит достаточно медленно. Причина этого в межмолекулярных столкновениях. Закон диффузии в жидкой и газообразной среде был найден немецким физиком Фиком:

dm = – D ·(dc / dl)· dS · dt.

Количество вещества dm, диффундирующее за время dt через элементарную площадку dS, перпендикулярную к направлению dl, вдоль которого происходит диффузия, пропорционально площади этой площадки, градиенту концентрации dc / dl и времени dt. Для газов коэффициент самодиффузии можно оценить из соотношения

D = (1/3)· v _ca·<λ>,

где v _ca – средняя арифметическая скорость частиц газа. Для различных газов при нормальных условиях D ≈ (10^–5 ÷ 10^–4) м²/с.

Внутреннее трение (вязкость) газов является проявлением сил трения между слоями газа, когда слои движутся с различными скоростями. Внутреннее трение в газах описывается законом Ньютона:

τ = – η·(dv / dz).

Здесь τ – напряжение трения, равное силе внутреннего трения, действующей на единицу поверхности газового слоя, η – коэффициент вязкости.

    Теплопроводность проявляется у газов при наличии градиента температур. Возникает направленный поток тепла из более горячей части объема в более холодную. Подсчет теплопроводности производится на основе закона Фурье:

d Q = – K ·(dT / dl)· dS · dt.

Таким образом определяется количество теплоты, проходящей через элементарную площадку dS, нормальную к направлению переноса dl за время dt. Здесь dT – разность температур, (dT / dl) – градиент температур в направлении переноса, К – коэффициент теплопроводности.

 

ВОПРОСЫ ДЛЯ КОНТРОЛЯ ЗНАНИЙ

1. Какой газ называется идеальным? Запишите уравнение состояния идеального газа.

2. Сколько молекул содержится в 1 моле вещества.

3. Что называется степенью свободы? Каково число степеней свободы у молекул идеального газа?

4. Что называется внутренней энергией идеального газа?

5. Что такое средняя длина свободного пробега частиц газа?

6. Каковы основные закономерности явлений переноса в газах: диффузии, вязкости, теплопроводности?

7. В чем состоит содержание первого начала термодинамики?

8. Какие изопроцессы, протекающие в газовой среде, Вы знаете?

9. Какие процессы называют круговыми (циклами)?

10.  Что представляет из себя машина Карно?

11.  Из каких процессов состоит цикл Карно?

12.  Сформулируйте нулевое начало термодинамики.

13.  Второе начало термодинамики, его формулировки. Понятие об энтропии.

 

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Электростатика

Основные понятия и законы электростатики

Существует два рода электрических зарядов – положительные и отрицательные. Принятое деление является условным. Исторически сложилось так, что заряды, возникающие на стекле, натираемом шелком, назвали положительными, а заряды на эбоните, натираемом о мех, назвали отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются. Носителями отрицательных зарядов в атоме являются электроны, носителями положительных зарядов – протоны, входящие в состав ядра атома. Алгебраическая сумма положительных и отрицательных зарядов в атоме равна нулю. Заряды располагаются таким образом, что атом в целом является нейтральным. Процесс электризации заключается в том, что заряды разного знака распределяются неравномерно между телами. Электрические заряды не создаются и не исчезают; они могут перемещаться от одного тела к другому или смещаться внутри тела или молекул. В этом состоит закон сохранения заряда. Носителями заряда в различных средах могут быть электроны, оторванные от атомов, или ионы – части молекул или атомов, имеющие положительные или отрицательные заряды. Величина любого заряда по абсолютной величине кратна заряду электрона. В системе СИ заряд измеряется в кулонах (Кл); 1 Кл – это электрический заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Заряд электрона имеет наименьшую возможную величину. Эта наименьшая порция заряда (1,6·10^-19 Кл) называется элементарным зарядом. Положительный заряд протона имеет ту же величину. Чисто электрическое притяжение или отталкивание наблюдается только у покоящихся зарядов. Взаимодействие зарядов зависит от их величины и взаимного расположения. Раздел физики, в котором рассматриваются такие взаимодействия, называется электростатикой. Поля, создаваемые покоящимися зарядами, как и силы их взаимодействия, принято называть электростатическими. Закон взаимодействия двух точечных зарядов был сформулирован Кулоном. Приведем формулировку этого закона. Два заряженных точечных тела взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению. Величина электростатической силы F прямо пропорциональна произведению зарядов тел и обратно пропорциональна квадрату расстояния r между ними:

F = q ₁ q ₂/(4π·ε_oε r ²).

Здесь q ₁, q ₂ – электрические заряды тел; ε_o – электрическая постоянная, ее численное значение 8,85·10^-12 Ф/м. При тех же источниках электрического поля его напряженность в веществе будет в ε раз меньше, чем в вакууме. Значения относительной диэлектрической проницаемости ε среды можно найти в справочниках. Для вакуума ε = 1, для масла ε = 5, слюды, стекла ε = 6, воды ε = 81. Количественной характеристикой силового действия электрического поля на заряды служит векторная величина Е – напряженность электрического поля. Она равна отношению силы F, действующей со стороны поля на неподвижный положительный пробный точечный электрический заряд, помещенный в рассматриваемую точку поля, к величине этого заряда: E = F / q. Величину напряженности поля точечного заряда можно найти из соотношения

E = q /(4π·ε_oε r ²).

Если коэффициент пропорциональности 1/(4π·ε_o) в законе Кулона обозначить через k _o ≈ 9·10⁹ Н·м²/Кл², закон Кулона и выражение для напряженности поля точечного заряда в вакууме приобретают вид

F = k _o q ₁ q ₂/ r ²;        E = k _o q / r ².

На заряд, не входящий в систему, действует сила, равная векторной сумме сил, с которыми действует на данный заряд каждый из зарядов системы в отдельности. В этом случае напряженность поля системы зарядов находится как векторная сумма напряженностей, создаваемых каждым зарядом в отдельности. Сформулированное правило называют принципом суперпозиции электрических полей. Поток вектора напряженности электрического поля через замкнутую поверхность пропорционален алгебраической сумме заключенных внутри этой поверхности зарядов (теорема Гаусса), для вакуума это записывается в виде:

.

Электрическое поле принято изображать графически в виде силовых линий. Густота этих линий пропорциональна модулю вектора напряженности. Направление силовых линий в каждой точке поля совпадает с направлением вектора электрической напряженности . Вектор напряженности направлен в ту же сторону что и сила, действующая со стороны поля на положительный пробный заряд, помещенный в данную точку. Интеграл  берется по поверхности S_G, охватывающей суммарный заряд q _вн. Фактически, поток Ф _Е – это только другое название числа силовых линий, пронизывающих поверхность воображаемую гауссову поверхность S _G.

    Использование теоремы Гаусса позволяет найти напряженности электрических полей, образованных различными заряженными телами. Для примера рассмотрим вычисление напряженности электрического поля положительно заряженной проводящей сферы радиусом R    (рис. 19). Поверхностная плотность заряда на сфере σ = q / S.

Рис. 19. Поле заряженной проводящей сферы

 

Как следует из теоремы Гаусса, вспомогательная поверхность S_G может быть любой формы, но она должна охватывать заряд. Заряд расположен на шаре симметрично. Поле заряда имеет сферическую симметрию. Вектор Е вне поверхности, охватываемой сферой, в каждой точке направлен по продолжению ее радиуса R. Поэтому выберем вспомогательную поверх

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: