 |
Сложение колебаний, биения. Затухающие колебания
|
|
|
|
Сложим колебания одного направления, имеющие одинаковую амплитуду, но совершающиеся с различной частотой. Начальная разность фаз складываемых колебаний равна нулю. Одно из колебаний совершается по закону 
, а другое – по закону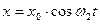 
. Результат сложения имеет вид
.
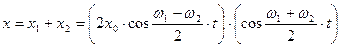В возникшем колебательном движении трудно определить какую-либо периодичность, но один частный случай представляет особый интерес. При сложении колебаний с близкими частотами, когда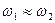 
, оказывается, что 
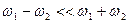. В этом случае сомножитель 
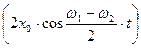можно рассматривать как медленно меняющуюся амплитуду колебаний, происходящих с частотой 
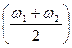. Такие колебания называются биениями. Их вид показан на рис. 14.
Рис. 14. Биения
В реальных системах, не содержащих источников энергии, колебания затухают. Это означает, что их амплитуда уменьшается со временем. Формально и затухающие процессы можно описывать функцией вида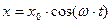 
, но амплитуда колебаний х о уже не является константой. Под воздействием трения она уменьшается. Экспериментально установлено, что сила трения F в первом приближении пропорциональна скорости v колебательного движения. Коэффициент пропорциональности α в соотношении F = α· v называется коэффициентом сопротивления. В этом случае затухающие колебания пружинного маятника можно описывать уравнением вида
.
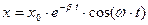Здесь х о – начальная амплитуда колебаний в момент времени t = 0. Величину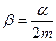 
называют коэффициентом затухания. Через время t после начала колебаний их амплитуда уменьшается в ℮ -β t раз. Амплитуда колебаний уменьшается в ℮ раз, если β t = 1. Время, необходимое для такого затухания, определяется как τ=1/β и называется временем релаксации. Логарифмический декремент затухания δ равен натуральному логарифму отношения амплитуды предыдущего колебания к амплитуде последующего. Можно показать, что
|
|
|
δ = β· t = Т /τ = 1/ N,
где N – число колебаний, в течение которых амплитуда уменьшается в ℮ раз. Частота затухающих колебаний при прочих равных условиях всегда несколько ниже частоты собственных незатухающих колебаний системы. Если затухание в системе не очень велико, то справедливо соотношение Q –1 = δ/π. Величина Q называется добротностью колебательной системы. Чем выше добротность, тем меньше затухание в системе. График затухающих колебаний приведен на рис. 15.
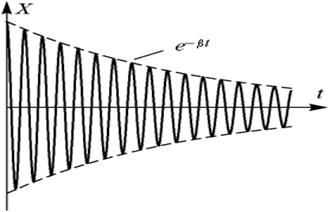
Рис. 15. Затухающие колебания
ВОПРОСЫ ДЛЯ КОНТРОЛЯ ЗНАНИЙ
1. Что называют системой отсчета?
2. Что такое: путь, перемещение, траектория?
3. Скорости: средняя, мгновенная; единицы их измерения.
4. Ускорения: среднее, мгновенное; составляющие ускорения; единицы их измерения.
5. Связь угловых и линейных характеристик движения.
6. Физический смысл массы в механике. Что называется импульсом материальной точки?
7. Законы Ньютона; границы их применимости.
8. Инерциальные системы отсчета. Приведите примеры.
9. Какие силы называются внешними; внутренними? Какие системы материальных точек называются замкнутыми?
10. Закон сохранения импульса.
11. Работа. Энергия.
12. Потенциальная энергия.
13. Консервативные силы.
14. Определение момента силы и момента импульса относительно оси.
15. Закон сохранения момента импульса.
16. Основной закон динамики вращательного движения.
17. Кинетическая энергия твердого тела, вращающегося вокруг
неподвижной оси.
18. Как записываются преобразования Галилея? Сложение скоростей в классической механике.
19. Постулаты специальной теории относительности.
20. Преобразования Лоренца.
21. Релятивистские выражения для массы, импульса, кинетической энергии.
|
|
|
22. Гармонические колебания и их характеристики: амплитуда, фаза, период, частота.
23. Что такое фазовый портрет гармонического осциллятора?
24. Что такое адиабатический инвариант?
25. Скорость и ускорение материальной точки, совершающей гармонические колебания.
26. Каков механизм распространения волн в упругих средах?
27. Как связаны между собой фазовая скорость волны, частота колебаний и длина волны?
28. Что такое фазовая и групповая скорости волны?
|
|
|
