 |
Расчет стоимости облигаций
|
|
|
|
Формула для расчета стоимости облигаций с постоянным купоном и постоянной ставкой дисконтирования (требуемая норма прибыли) выглядит следующим образом:
|
где V – стоимость; D = N ´ k – доход, в денежных единицах; N – номинальная стоимость облигации; k – годовая ставка купона; r – ставка дисконтирования; i – год; D – доход; п – число лет; m – число купонных выплат в году.
ПРИМЕР 1.
Продается облигация номиналом 1000 руб. Выплата процентов производится 1 раз в год. Процентная (купонная) ставка составляет 20 % годовых. До погашения облигации остается ровно 5 лет. Требуемая норма прибыли (доходность) на инвестиции с учетом риска, соответствующего данному типу облигаций, составляет 15 %. Определить стоимость облигации.
Решение
В конце каждого года держатель облигации получит процентный доход в размере 200 руб., а в конце 5-го года – еще и сумму, равную номиналу облигации, т.е. 1000 руб. Определим дисконтированные (приведенные) стоимости доходов для каждого года и найдем их сумму. Приведенная стоимость платежей (стоимость облигации) составит (см. формулу для V):
V = 
+ 
+ 
+ 
+ 
=
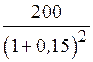= 173,9 + 151,5 + 131,5 + 114,9 + 597,0 = 1168,8 (руб.).
Формула для расчета стоимости облигаций с постоянным купоном и изменяющейся ставкой дисконтирования (требуемой нормой прибыли).
В случае если ставка дисконтирования изменяется (например, ОФЗ-ПД), для определения приведенной стоимости облигаций требуется найти продисконтированные потоки доходов для каждого года, используя следующую формулу:
|
|
|
где V – приведенная стоимость дохода i -го года; D – доход по купону; r 1, r 2,¼, ri – ставка дисконтирования для 1-го, 2-го,..., i -го года; N – номинальная стоимость облигации.
ПРИМЕР 2
По облигации номиналом 1000 руб. выплачивается 20 % годовых. Выплата процентов производится 1 раз в год. До погашения облигации остается 5 лет. Требуемая норма прибыли в течение первых 3 лет – 20 %, 4-й год –15%, 5-й год – 10 %. Определить стоимость облигации.
Решение
Процентный доход каждого года и сумму погашения облигации необходимо продисконтировать по переменной ставке дисконтирования. Определим дисконтированные стоимости для платежей каждого года:
V = 
+ 
+ 
+ 
+
+ 
= 166 + 138,9 + 115,7 + 101,0 + 603,0 = 1124,6 руб.
В случае если процентный доход по облигациям выплачивается не один, а несколько раз в год, формула будет иметь следующий вид:
где m – число выплат процентного дохода в течение года; n – число лет; N – номинал облигации; D – процент дохода в денежных единицах.
ПРИМЕР 3
Номинал облигации – 1000 руб. Процентная ставка – 20% годовых. Выплата процентов производится 2 раза в год. До погашения облигации остается 5 лет. Определить курсовую стоимость облигации, если требуемая норма прибыли составляет 15 % годовых.
Решение
руб.
Формула для расчета стоимости облигаций с плавающим купоном
Данная формула может быть использована для расчета (облигаций федерального займа (ОФЗ-ПК), облигаций государственного сберегательного (ОГСЗ).
где D 1,2,¼, п – процентный доход i -го периода (i = 1,2, ..., n); r 1,2,¼, п – требуемая норма прибыли (ставка дисконтирования) i -го периода.
ПРИМЕР 4
Номинал облигации – 1000 руб. До погашения остается 3 года. Процентный доход выплачивается 2 раза в год. По первому купону выплачивается 22 % годовых. Определите рыночную стоимость облигации при условии, что купонная ставка будет снижаться: 1-й год – 22 % годовых, 2-й год – 20 %, 3-й год – 18 % Будет снижаться и требуемая норма прибыли: 1-й год – 22 % годовых, 2-й год – 21 %, 3-й год – 19 %.
|
|
|
Решение
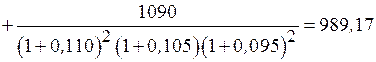руб.
Доходность облигаций
Текущая доходность характеризует отношение текущих поступлений по облигации в данном году к зафиксированной на момент изменения показателя рыночной стоимости облигации. В частности, текущая доходность облигации с фиксированной ставкой купона определяется как отноение периодического платежа к цене приобретения
где Rt – текущая доходность; D = N ´ k – доход, в денежных единицах; N – номинальная стоимость облигации; k – годовая ставка купона; Р – текущая рыночная цена облигации.
ПРИМЕР 5
Облигация номиналом 1000 руб. продается по цене 400 руб., процентный доход в размере 10% годовых выплачивается 1 раз в год.
Решение
Текущая доходность будет равна:
, или 25,0 % годовых.
Параметр текущей доходности, как правило, непригоден при сравнении инвестиционных качеств разных видов облигаций, так как он не учитывает все элементы денежного потока по облигации. Наиболее информативным параметром для оценки инвестиционной привлекательности и анализа облигаций является показатель доходности к погашению.
Доходность к погашению ( yield to maturity (YTM = r )) учитывает все элементы денежного потока по облигациям, заданные условиями эмиссии. Этот показатель измеряет эффективность инвестиций в облигацию для инвестора в виде годовой процентной ставки (нормы дисконта), устанавливающей равенство между текущей стоимостью потока платежей по облигации и ее рыночной ценой V, которая определяется выражением вида
|
|
Если известна цена облигации, то доходность к погашению можно определить методом последовательных приближений. На основе вычисленной доходности к погашению можно решать вопрос о приемлемости тех или иных инвестиций. Если инвестор определил для себя требуемую норму прибыли для данного вида вложений (с учетом риска) и если полученная норма прибыли по облигации равна или выше требуемой номы, то покупка облигаций является выгодным вложением средств.
|
|
|
В частном случае доходность к погашению бескупонной облигации (облигации с нулевым купоном) определяется из формулы:
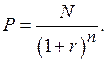
После преобразований получаем:
ПРИМЕР 6
Цена облигации – 600 руб., номинал – 1000 руб. До погашения облигации остается 5 лет. Определить доходность к погашению, если доход по купонным облигациям выплачивается 1 раз в год.
Решение
Доходность к погашению краткосрочных облигаций(сроком действия до 1 года) обычно определяется по формуле:
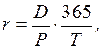
где D – величина дисконта (процентного дохода) в денежных единицах; Р – цена облигации; Т – число дней до погашения облигации.
Подставляя вместо D = N – Р,получаем:
или
где N – номинал облигации.
ПРИМЕР 7
Облигация номиналом 1000 руб. продается с дисконтом по цене 930 руб. До погашения облигации остается 50 дней. Определить доходность к погашению, если погашение происходит по номиналу.
Решение
Rt = (1000 / 930 - 1) ´ (365 / 50) = 0,5495, или 54,95%
|
|
|
