 |
1. Переменные величины и функции при изучении природных систем. Методы визуализации натурных данных. Графики изменчивости переменных величин.
|
|
|
|
1. Переменные величины и функции при изучении природных систем. Методы визуализации натурных данных. Графики изменчивости переменных величин..
Методы визуализации могут быть разделены на представления данных в одном, двух и трёх измерениях. Наиболее распространена двумерная визуализация — изображение на плоскости, на листе бумаги — или на экране. Однако, благодаря развитию компьютерной техники и программного обеспечения всё большую роль начинают играть методы объёмной (3D)-визуализации, как динамической (анимация, псевдостереоскопия) так и стереоскопической.
Графики предназначены прежде всего для иллюстрирования математических понятий, функциональных зависимостей или связей между объектами.
Диагра́ мма - графическое представление данных, позволяющее быстро оценить соотношение нескольких величин. Представляет собой геометрическое символьное изображение информации с применением различных приёмов техники визуализации.
Карта — изображение земной поверхности, содержащее координатную сетку с условными знаками на плоскости в уменьшенном виде, отображающее размещение, состояние и связи различных природных и общественных явлений, их изменения во времени, развитие и перемещение.
Визуализация в ГИС — процесс проектирования и генерации изображений на устройствах отображения, преобразование цифровых данных в изображение на основе определённых правил и алгоритмов.
2. Методы интерполяции экспериментальных данных - линейная и квадратичная. Задачи экстраполяции.

Пусть известные значения некоторой функции f образуют следующую таблицу:
| х | x0 | x1 | … | xn |
| f(x) | y0 | y1 | … | yn |
При этом требуется получить значение функции f для такого значения аргумента х, которое входит в отрезок [x0; xn], но не совпадает ни с одним из значений xi (i=0, 1, …, n). Проще говоря, задача интерполяции состоит в том, чтобы понять какое у в точке х, еслт нет такого значения в измеренных данных.
|
|
|
Классический подход к решению задачи построения приближающей функции основывается на требовании строгого совпадения значений f(x) и F(x) в точках xi(i=0, 1, 2, …, n), т. е.
F(x0)=y0, F(x1)=y1, …, F(xn)=yn
В этом случае нахождение приближенной функции называют интерполяцией (или интерполированием), а точки x0, x1, …, xn – узлами интерполяции. Геометрически это означает, что нужно найти кривую y=F(x) некоторого определенного типа, проходящую через заданную систему точек Mi(xi, yi) (i=0, 1, 2, …, n). В случае, если x не принадлежит [x0, xn] нахождение искомой функции называют экстраполяцией. В дальнейшем, под термином интерполяция будем понимать как первую, так и вторую операции.
Наиболее удобной в практическом использовании функцией является алгебраический многочлен степени n:
Pn(x)=a0xn + a1xn-1 + … + an-1x + an
Чтобы задать многочлен n-ой степени достаточно задать его n+1 коэффициент. Значения многочлена просто вычисляются, его легко продифференцировать, проинтегрировать и т. д. Поэтому алгебраические многочлены нашли широкое применение для приближения функций.
1. Линейная интерполяция.
Итак, пусть мы имеем функцию, заданную таблично. Решая задачу интерполяции, найдем в таблице два соседних значения аргумента (обозначим их хk и xk+1), между которыми лежит заданное значение х (хk< x< xk+1), пусть yk=f(xk) и yk+1=f(xk+1) – соответствующие им значения функции. Будем считать, что в промежутке (хk, xk+1) данную функцию с достаточной степенью точности можно заменить линейной функцией, т. е. дугу графика функции можно заменить стягивающей ее хордой. Такая замена называется линейной интерполяцией.
|
|
|

Уравнение прямой – у=K*х +b.
По графику

«+» - не даст больших погрешностей
«-» - нельзя применять когда интервалы между измерениями разные.
2. Квадратичная интерполяция.
Пусть снова дана функция f(x), заданная таблично. Считая, что на промежутке (xk, xk+2) данную функцию с достаточной степенью точности можно заменить квадратичной функцией, то есть часть графика функции можно заменить параболой (см. рис. 3), необходимо найти значение функции f(x) в некоторой точке x, принадлежащей интервалу (xk, xk+2).
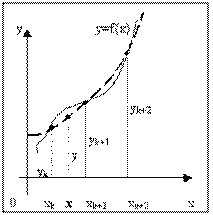
Будем искать квадратичную функцию в следующем виде: 
Исходя из условия совпадения значений искомой квадратичной функции с табличными значениями функции в трех заданных точках, составим следующую систему уравнений:
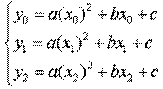
Это система трех линейных уравнений с тремя неизвестными a, b и с. Ее определитель не равен 0 (если только точки не лежат на одной прямой). Решая составленную систему уравнений матричным способом, получим следующую зависимость для коэффициентов а, b и с:

Таким образом значение функции f(х) в точке х можно приближенно считать равным

-
|
|
|


