 |
Общее представление о формуле Тэйлора. Численный расчет градиентов таблично заданных функций. Расчет старших производных.
|
|
|
|
Билет 8
Общее представление о формуле Тэйлора. Численный расчет градиентов таблично заданных функций. Расчет старших производных.
Градиент: Допустим, у нас есть измеренные данные температуры T1…Ti по времени t1... ti, градиент исследуемой величины будет рассчитываться 
общий вид производной
В общем трёхмерном случае градиент – это вектор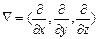 
. Но т. к. мы работаем с большими массивами точек, то решать градиент в общем виде сложно, мы рассматриваем градиент по одной переменной – это есть производная в i-точке по направлению х. 
.
Формула Тейлора
Рассмотрим функцию f(x)
Ф. Тейлора связывает функцию и многочлен приближенно.
Точность - 
, степень 
у отбрасываемого наибольшего члена называется порядком точности соответствующей формулы.
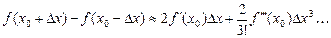(все четные убираются) – несим.
Разделим на 2∆ х.
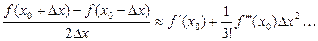(2-ой порядок точности)
Первая производная: 
- симметричная функция
(делим на Δ x2)
Вторая производная: 
где 
- бесконечно малое
Ф. Тейлора является эффективным генератором получения формул для вычисления производных любого порядка.
Билет 9
Дифференциальные уравнения первого и второго порядков: основные определения и способы решений. Общее и частное решения.
Обыкновенным дифференциальным уравнением n – го порядка для функции y аргумента x называется соотношение вида
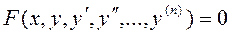(1. 1),
где F – заданная функция своих аргументов. В названии этого класса математических уравнений термин «дифференциальное» подчеркивает, что в них входят производные 
(функции, образованные как результат дифференцирования); термин – «обыкновенное» говорит о том, что искомая функция зависит только от одного действительного аргумента.
|
|
|
Обыкновенное дифференциальное уравнение может не содержать в явном виде аргумент x, искомую функцию 
и любые ее производные, но старшая производная 
обязана входить в уравнение n-го порядка. Например
а)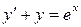 
– уравнение первого порядка;
б) 
– уравнение третьего порядка.
При написании обыкновенных дифференциальных уравнений часто используются обозначения производных через дифференциалы:
в) 
– уравнение второго порядка;
г) 
– уравнение первого порядка,
образующее после деления на dx эквивалентную форму задания уравнения: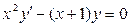 
.
Функция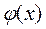 
называется решением обыкновенного дифференциального уравнения, если при подстановке в него 
оно обращается в тождество.
Например, уравнение 3-го порядка
имеет решение 
.
Найти тем или иным приемом, например, подбором, одну функцию, удовлетворяющую уравнению, не означает решить его. Решить обыкновенное дифференциальное уравнение – значит найти все функции, образующие при подстановке в уравнение тождество. Для уравнения (1. 1) семейство таких функций образуется с помощью произвольных постоянных и называется общим решением обыкновенного дифференциального уравнения n-го порядка, причем число констант совпадает с порядком уравнения: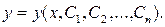 
Общее решение может быть, и не разрешено явно относительно y(x): 
В этом случае решение принято называть общим интегралом уравнения (1. 1).
Например, общим решением дифференциального уравнения 
является следующее выражение: 
, причем второе слагаемое может быть записано и как 
, так как произвольная постоянная 
, делённая на 2, может быть заменена новой произвольной постоянной 
.
Задавая некоторые допустимые значения всем произвольным постоянным в общем решении или в общем интеграле, получаем определенную функцию, уже не содержащую произвольных констант. Эта функция называется частным решением или частным интегралом уравнения (1. 1). Для отыскания значений произвольных постоянных, а следовательно, и частного решения, используются различные дополнительные условия к уравнению (1. 1). Например, могут быть заданы так называемые начальные условия при 
(1. 2)
|
|
|
В правых частях начальных условий (1. 2) заданы числовые значения функции и производных, причем, общее число начальных условий равно числу определяемых произвольных констант.
Задача отыскания частного решения уравнения (1. 1) по начальным условиям называется задачей Коши.
|
|
|
