 |
5. Общее представление о рядах Фурье. Гармонический анализ временных рядов
|
|
|
|
5. Общее представление о рядах Фурье. Гармонический анализ временных рядов
Многие природные процессы являются периодическими, т. е. воспроизводятся в прежнем виде через определенный промежуток времени Т (смена времен года, смена дня и ночи, продолжительность светового дня и т. д. ). С точки зрения математики, различные величины, связанные с рассматриваемыми периодическими процессами, по истечение периода Т возвращаются к своим прежним значениям и являются периодическими функциями от времени t: 
Гармонический анализ – это процесс разложения периодической функции в ряд Фурье (на гармоники). Гармоника (гармонические составляющие функции f(t)) – отдельные синусоидальные величины, входящие в состав тригонометрического ряда. Ибо периодическая функция f(t) периода Т (при этом составляющие синусоидальные величины разных частот) может быть представлена в виде суммы конечного или бесконечного множества синусоид. Интерпретация полученных результатов: с помощью гармонического анализа можно выделить низко-, средне- и высокочастотные колебания, а также оценить вклад отдельных гармоник в исследуемый процесс.
Задача гармонического анализа заключается в построении практически удобных методов для приближенного определения коэффициентов ряда Фурье или для непосредственного вычерчивания гармоник различных порядков для функции, заданной таблично. По этим коэффициентам можно судить о вкладе отдельных гармоник: если k≈ 0, то вклад гармоник минимальный, а если k≈ 1, то это основные гармоники. По ним можно составлять гипотезы и процессооформирующих явлениях.
Пусть ф-ия f(x) – периодическая с периодом 2π: f(x+2π )=f(x). Основная задача гармонического анализа – представить ф-цию f(x) в виде ряда: 
, где коэф. ряда определяется по формулам Эйлера-Фурье: 
; 
; 
|
|
|
Полагая что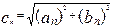 
, 
, 
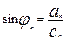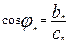ряд можно представить в ви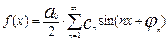де: 
, где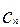 
- амплитуда гармоники, 
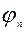- фаза
6. Сглаживание и фильтрация временных рядов. Определения и основные алгоритмы.
Ряд Фурье и гармонический анализ позволяют выполнить фильтрацию временного ряда. Напр.:
*Если обнулить n-компонент (с низкими частотами), то это высокочастотная фильтрация;
*Если удалить все компоненты с какой-то высокой частотой, то это будет низкочастотная фильтрация;
*Обнулив компонент со значениями частот «от и до» - полосовая фильтрация.
Иногда фильтрация с пропусканием высоких частот производится путем вычитания сглаженных величин из данного ряда, в рез-те в ряду остаются только высокие частоты.
1)Фильтрация низких и высоких частот, в рез-те чего в ряду остаются средние частоты. Иногда эти частоты получаются путем дополнительного сглаживания ряда данных, полученных путем вычитания первоначального сглаживания величин из экспериментального ряда.
2)Существуют фильтры позволяющие усилить высокие частоты. Этим достигается ликвидация эффекта предыдущего сглаживания (процесс «обратного сглаживания»).
Простейшими фильтрами являются скользящая средняя и взвешенная скользящая средняя.
Билет 7
Численное интегрирование временных рядов. Методы прямоугольников и трапеций. Погрешности.
Значение определенного интеграла численно равно площади криволинейной трапеции, ограниченной графиком функции y=f(x), осью абсцисс и прямыми х=а, х=b. Находя приближенно площадь криволинейной трапеции, мы получаем значение интеграла. Формально процедура численного интегрирования заключается в том, что отрезок [а, b] разбивается на n частичных отрезков, а затем подинтегральная функция заменяется на нем легко интегрируемой функцией, по определенной зависимости интерполирующей значения подинтегральной функции в точках разбиения.
|
|
|
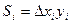- площадь левого прямоугольника
- площадь правого прямоугольника
- площадь трапеции
Итак, функция у=f(x) интегрируема на сегменте [a, b] и требуется вычислить ее интеграл 
. Составим интегральную сумму для f(x) на сегменте [a, b]. Для этого разобьем сегмент [a, b] на n равных между собой частей с помощью точек: x1, x2, …, xk, …, xn-1.
Если длину каждой части мы обозначим через Dх, так что 
, то для каждой точки xiбудем иметь: 
(i=0, 1, 2, …, n).
Обозначим теперь через yi значение подынтегральной функции f(x) при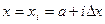 
, то есть положим 
(i=0, 1, …, n).
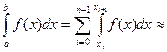
- формула левых прямоугольников или
- формула правых прямоугольников.
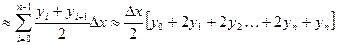- формула трапеции
Метод прямоугольников – это наиболее простой и вместе с тем наиболее грубый метод приближенного интегрирования. Заметно меньшую погрешность дает метод трапеций.
|
|
|
