Метод Эйлера решения обыкновенных дифференциальных уравнений.

Билет 10

Метод Эйлера решения обыкновенных дифференциальных уравнений.

В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения. Этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Идея метода заключается в том, что на малом промежутке изменения независимой переменной

интегральная кривая дифференциального уравнения

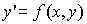(8)

заменяется отрезком прямой (касательной)

.

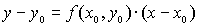Отсюда 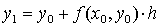и процесс можно повторить для промежутка и т. д. Число h является здесь шагом таблицы.

Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера (рис. 13).

Рис. 13

Рабочая формула для определения значений у по методу Эйлера имеет вид

(9)

где

Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага, вообще говоря, систематически возрастает. Наиболее приемлемым для практики методом оценки точности является в данном случае метод двойного счета – с шагом h и с шагом h/2. Совпадение десятичных знаков в полученных двумя способами результатах дает естественные основания считать их верными. Ошибка метода пропорциональна h². Существуют различные уточнения метода Эйлера, повышающие его точность так, что ошибка метода становится пропорциональной h³([13]).

 

Билет 11

Метод Рунге-Кутта решения обыкновенных дифференциальных уравнений.

 

Пусть дано дифференциальное уравнение первого порядка

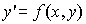
с начальными условиями y(x₀)=y₀. Выберем шаг h и для краткости введем обозначения x_i=x₀+ih и y_i=y(x_i), (i=0, 1, 2, …).

В вычислительной практике наиболее часто используется метод Рунге-Кутта. Приведем без вывода один из вариантов соответствующих расчетных формул:

(9)

Последовательные приближения y_i искомой функции y определяются по формуле:

y_i+1=y_i+ y_i

где

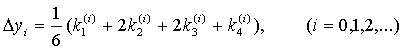(10)

Отметим, что в этом случае погрешность на шаге пропорциональна пятой степени шага (h⁵). Отсюда, в частности, следует, что при достаточно малом h и малых погрешностях вычислений решение уравнения (1), полученное методом Рунге-Кутта по формулам (9), будет близким к точному.

Геометрическим смысл использования метода Рунге-Кутта с расчетными формулами (9) состоит в следующем. Из точки (x_i, y_i) cдвигаются в направлении, определяемом углом ₁, для которого tg ₁=f(x_i, y_i). На этом направлении выбирается точка с координатами (x_i+h/2, y_i+k₁/2). Затем из точки (x_i, y_i) cдвигаются в направлении, определяемом углом ₂, для которого tg ₂=f(x_i+h/2, y_i+k₁/2), и на этом направлении выбирается точка с координатами (x_i+h/2, y_i+k₂/2). Наконец, из точки (x_i, y_i) cдвигаются в направлении, определяемом углом ₃, для которого tg ₃=f(x_i+h/2, y_i+k₂/2) и на этом направлении выбирается точка с координатами (x_i+h, y_i+k₃). Этим задается еще одно направление, определяемое углом ₄, для которого tg ₄=f(x_i+h, y_i+k₃). Четыре полученных направления усредняются в соответствии с последней из формул (9). На этом окончательном направлении и выбирается очередная точка (x_i+1, y_i+1)= (x_i+h, y_i+ y).

 

Билет 12

Метод Рунге-Кутта решения систем обыкновенных дифференциальных уравнений первого порядка.

Пусть дано дифференциальное уравнение первого порядка

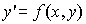
с начальными условиями y(x₀)=y₀. Выберем шаг h и для краткости введем обозначения x_i=x₀+ih и y_i=y(x_i), (i=0, 1, 2, …).

В вычислительной практике наиболее часто используется метод Рунге-Кутта. Приведем без вывода один из вариантов соответствующих расчетных формул:

(9)

Последовательные приближения y_i искомой функции y определяются по формуле:

y_i+1=y_i+ y_i

где

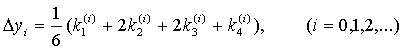(10)

Отметим, что в этом случае погрешность на шаге пропорциональна пятой степени шага (h⁵). Отсюда, в частности, следует, что при достаточно малом h и малых погрешностях вычислений решение уравнения (1), полученное методом Рунге-Кутта по формулам (9), будет близким к точному.

Билет№11

 

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: