Главная | Обратная связь | Поможем написать вашу работу!

Билет№ 12. Постановка задачи Коши

Билет№ 12

Пусть дано дифференциальное уравнение первого порядка

с начальными условиями y(x₀)=y₀. Выберем шаг h и для краткости введем обозначения x_i=x₀+ih и y_i=y(x_i), (i=0, 1, 2, …).

В вычислительной практике наиболее часто используется метод Рунге-Кутта. Приведем без вывода один из вариантов соответствующих расчетных формул:

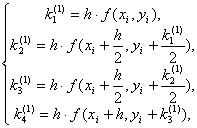(9)

Последовательные приближения y_i искомой функции y определяются по формуле:

y_i+1=y_i+ y_i

где

(10)

Отметим, что в этом случае погрешность на шаге пропорциональна пятой степени шага (h⁵). Отсюда, в частности, следует, что при достаточно малом h и малых погрешностях вычислений решение уравнения (1), полученное методом Рунге-Кутта по формулам (9), будет близким к точному.

Геометрическим смысл использования метода Рунге-Кутта с расчетными формулами (9) состоит в следующем. Из точки (x_i, y_i) cдвигаются в направлении, определяемом углом ₁, для которого tg ₁=f(x_i, y_i). На этом направлении выбирается точка с координатами (x_i+h/2, y_i+k₁/2). Затем из точки (x_i, y_i) cдвигаются в направлении, определяемом углом ₂, для которого tg ₂=f(x_i+h/2, y_i+k₁/2), и на этом направлении выбирается точка с координатами (x_i+h/2, y_i+k₂/2). Наконец, из точки (x_i, y_i) cдвигаются в направлении, определяемом углом ₃, для которого tg ₃=f(x_i+h/2, y_i+k₂/2) и на этом направлении выбирается точка с координатами (x_i+h, y_i+k₃). Этим задается еще одно направление, определяемое углом ₄, для которого tg ₄=f(x_i+h, y_i+k₃). Четыре полученных направления усредняются в соответствии с последней из формул (9). На этом окончательном направлении и выбирается очередная точка (x_i+1, y_i+1)= (x_i+h, y_i+ y).

Билет № 13

Если система совершает колебания под действием сил, развивающихся в самой колебательной системе без внешних воздействий и без учета сил сопротивления, то колебания называются незатухающими собственными колебаниями.

Отсутствие затухания колебаний характерно для идеальной колебательной системы, которая является физической моделью реальных физических процессов.

2. Дифференциальное уравнение, соответствующее колебаниям пружинного маятника, можно получить из закона его движения, которым является 2-й закон Ньютона m a = F.

Учитывая, что ускорение есть вторая производная от смещения по времени
,
а сила, действующая на тело, есть сила упругости, определяемая для малых смещений тела от положения равновесия по закону Гука, как 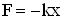, получим

или
.

Это дифференциальное уравнение второго порядка для незатухающих колебаний. Основной его отличительной особенностью является тот факт, что вторая производная от смещения по времени (т. е. ускорение) пропорциональна смещению. Дифференциальное уравнение, в которое величина х входит в нулевой или первой степени, называется линейным дифференциальным уравнением. В дальнейшем мы покажем, что подобного рода уравнения характерны для незатухающих колебаний в любой идеальной колебательной системе. Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести F_τ = –mg sin φ (рис. 2. 3. 1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.

Перенесем все члены уравнения в левую часть и приведем дифференциальное уравнение к виду:

3. Решением дифференциального уравнения такого вида являются уравнения:

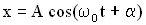или

Эти решения называются уравнениями колебаний, они позволяют вычислить смещение х пружинного маятника в любой момент времени.

Колебания, при которых характеризующие их физические величины изменяются по закону синуса или косинуса, называются гармоническими.

Билет №14

Постановка задачи Коши

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида

(1)

Решением дифференциального уравнения является некоторая функция y(x), которая при подстановке в выражение обращает его в тождество. Существует множество решений (так называемых частных решений) дифференциального уравнения (1), которые могут быть объединены и записаны в виде общего решения

y=y(x, C), (2)

где С – произвольная постоянная. Геометрически это можно интерпретировать как семейство интегральных кривых, каждая из которых является графиком решения (1)

ля выбора одной кривой из семейства (частного решения y=y(x, c)) необходимо задать начальные условия

y(x₀)=y₀, (3)

то есть одну точку на искомой кривой решения.

Как правило, практическое значение имеет всегда частное решение дифференциального уравнения. Задача нахождения частного решения уравнения (1), соответствующего начальным условиям (3), называется задачей Коши.

В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения. Этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Идея метода заключается в том, что на малом промежутке изменения независимой переменной

интегральная кривая дифференциального уравнения

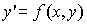(8)

заменяется отрезком прямой (касательной)

Отсюда 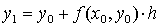и процесс можно повторить для промежутка и т. д. Число h является здесь шагом таблицы.

Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера

Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага, вообще говоря, систематически возрастает. Наиболее приемлемым для практики методом оценки точности является в данном случае метод двойного счета – с шагом h и с шагом h/2. Совпадение десятичных знаков в полученных двумя способами результатах дает естественные основания считать их верными. Ошибка метода пропорциональна h². Существуют различные уточнения метода Эйлера, повышающие его точность так, что ошибка метода становится пропорциональной h³(

Билет № 15

Дифференциальное уравнение в частных производных (частные случаи также известны как уравнения математической физики, УМФ) — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.

Дифференциа́ льное уравне́ ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением.

Размерность: Равна количеству независимых переменных. Должна быть не меньше 2 (при 1 получается обыкновенное дифференциальное уравнение).

Линейность: Есть линейные и нелинейные уравнения. Линейное уравнение представимо в виде линейной комбинации производных от неизвестных функций. Коэффициенты при этом могут быть либо постоянными, либо известными функциями. Линейные уравнения хорошо исследованы, за решение отдельных видов нелинейных уравнений назначены миллионные премии (задачи тысячелетия). Однородность: Уравнение является неоднородным, если есть слагаемое, не зависящее от неизвестных функций. Порядок: Порядок уравнения определяется максимальным порядком производной. Имеют значение порядки по всем переменным. Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Произво́ дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю,

Моделирование процесса распространения загрязнения в водоёме без течения.

Процесс диффузии примесей в воде или воздухе описывается уравнением диффузии:

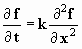где f - субъект загрязнения (соль, тепло, нефть, и т. п. ). k - коэффициент диффузии, t - время, x - пространственная координата. Такого рода уравнение решается по следующей конечно-разностной схеме: 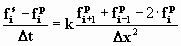или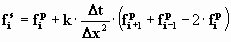

где индекс p - обозначает прошлый слой по времени, а s - следующий; индекс i -обозначает пространственную координату.

цикл по времени ( t )

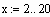цикл по пространству -( х )

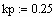коэффициент, определяемый значением коэффициента диффузии и величиной шагов по времени и пространству.

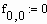
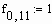начальное значение загрязнителя.

второй максимум.

Билет № 16

Сетевой график (стрелочная диаграмма, сетевая модель или просто сеть) состоит из стрелок и кружков, обозначающих два основных элемента любой сети – работы и события. Работа – это реальный процесс или действие, требующее затрат труда, материалов или времени. Продолжительность выполнения работ измеряется в единицах времени: часах, днях, неделях, месяцах и т. д. Работы могут иметь также и количественные показатели, которые характеризуют трудоемкость, стоимость, материальные ресурсы и т. д. Работы обозначаются стрелками, которые соединяются между собой с помощью кружков (событий). Временные и количественные оценки проставляются обычно над стрелками. Событием называется результат, получаемый после выполнения работ, стрелки которых сходятся к данному кружку. Событие имеет двойственное значение. Для всех предшествующих работ оно является законченным свершением, а для последующих работ – начальным пунктом их выполнения. Всем событиям присваивается определенный цифровой шифр, который проставляется обычно внутри кружка. В общем смысле начальное (предшествующее) событие обозначается буквой i, а конечное (последующее) буквой j, работа в этом случае обозначается как i, j

Во всяком сетевом графике бывает два особых события, которые не имеют двойственного значения – исходное и завершающее. Исходное событие – это момент начала выполнения комплекса работ. Оно не является результатом предыдущих работ, поэтому в него не входит ни одной стрелки. Исходные события принято обозначать буквой J. К особенностям завершающего события относится то, что оно свидетельствует об окончании всех работ и поэтому не имеет ни одной последующей работы. Из этого события не выходит ни одной стрелки. Обозначается оно буквой С.

Билет№ 17

Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Среди различных путей сетевого графика наибольший интерес представляет полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим. Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути. По существу, критический путь – " узкое" место проекта. Уменьшить общую продолжительность осуществления проекта можно, только изыскав способы сокращения работ, лежащих на критическом пути. Таким образом, нет никакой необходимости в часто практикуемом стремлении " поднажать" на всех работах ради сокращения общей длительности выполнения проекта. В больших проектах критическими бывают примерно 10% работ. Для рассмотренного в примере 1 сетевого графика полными путями будут:

путь 1 2 4 7 8 (продолжительностью 10+30+0+20=60 минут), путь 1 2 5 6 7 8 (продолжительностью 10+0+40+0+20=70 минут), путь 1 3 4 7 8 (продолжительностью 20+0+0+20=40 минут), путь 1 3 5 6 7 8 (продолжительностью 20+20+40+0+20=100 минут). Последний путь имеет наибольшую продолжительность и является критическим. Продолжительность критического пути составляет 100 минут. Быстрее работу выполнить нельзя, так как для достижения завершающего события критический путь надо пройти обязательно.

Время, необходимое для выполнения некритических работ, не имеет значения с точки зрения продолжительности осуществления проекта в целом. Иначе говоря, все ненапряженные пути имеют резервы времени. Эти резервы опреде

Билет№ 18

Выполнение комплексных научных исследований, а также проектирование и строительство промышленных, сельскохозяйственных и транспортных объектов требуют календарной увязки большого числа взаимосвязанных работ, выполняемых различными организациями. Составление и анализ соответствующих календарных планов представляют собой весьма сложную задачу, при решении которой применяются так называемые методы сетевого планирования. По существу, этот метод дает возможность определить, во-первых, какие работы или операции из числа многих, составляющих проект, являются " критическими" по своему влиянию на общую календарную продолжительность проекта и, во-вторых, каким образом построить наилучший календарный план проведения всех работ по данному проекту с тем, чтобы выдержать заданные сроки при минимальных затратах. Идея сетевого метода очень проста. Она основана на графическом изображении комплекса работ с любой степенью их детализации и на выполнении элементарных арифметических операций по расчету параметров и анализу сетевых графиков.

⇐ Предыдущая 1 2 3 4 56

Воспользуйтесь поиском по сайту: