 |
3. Методы аппроксимации табличных данных. Невязки. Метод наименьших квадратов.
|
|
|
|
Из курса математики известны 3 способа задания функциональных зависимостей: 1) аналитический2) графический3) табличныйТабличный способ обычно возникает в результате эксперемента. Недостаток табличного задания функции заключается в том, что найдутся значения переменных которые неопределены таблицей. Для отыскания таких значений определяют приближающуюся функцию, называемой аппроксмирующей, а действие замены аппроксимацией.
Задача аппроксимации функции одной переменной с самого начала обязательно учитывает характер поведения исходной функции на всем интервале наблюдений. Формулировка задачи выглядит следующим образом. Функция у= f(х) задана таблицей
| х | x1 | х2 | … | xn |
| f(x) | y1 | у2 | … | yn |
Необходимо найти функцию заданного вида: y=F(x), которая в точках x1, x2, …, xn принимает значения, как можно более близкие к табличным y1, y2, …, yn.
По таблице строится точечный график f(x), затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек. По полученной таким образом кривой на качественном уровне устанавливается вид приближающей функции.
Рассмотрим рисунок:



 У (а) У (b) У (с)
У (а) У (b) У (с)


































 | |||||||||||||||||
 |  | ||||||||||||||||
 |  |  |  | ||||||||||||||
 | |||||||||||||||||
 |  |  | |||||||||||||||
На рисунке изображены три ситуации:
|
|
|
1) график а - взаимосвязь х и у близка к линейной; прямая линия здесь близка к точкам наблюдений, и последние отклоняются от нее лишь в результате сравнительно небольших случайных воздействий.
2) график b - реальная взаимосвязь величин х и у описывается нелинейной функцией, и какую бы мы ни провели прямую линию, отклонение точек наблюдения от нее будет существенным и неслучайным. В то же время, проведенная ветка параболы достаточно хорошо отражает характер зависимости между величинами.
3) график с - явная взаимосвязь между переменными х и у отсутствует; какую бы мы ни выбрали формулу связи, результаты ее параметризации будут здесь неудачными. В частности, обе выбранные прямые одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной у по значениям переменной х.
Невязка – разница между эмпирическими значениями и значениями аппроксимирующих линий; или разница между наблюденными аппроксимирующих функций.
Поиск простейших эмпирических зависимостей необходим чтобы упорядочить значения системы, заменить одну систему координат на другую.
Z = axm
lnz = lna + m lnx соответственно Y = AX + B – линейная зависимость, а х = lnx и у = lnz – логарифмич замена. Переходим к билогарифмированию:

В естествознании часто используется метод наименьших квадратов - метод оценивания параметров приближающей функции, кот сводит к min сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции.
Метод наименьших квадратов
Метод наименьших квадратов (МНК) - Метод оценивания параметров приближающей функции, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции.
Задача приближения функции f: для функции f, заданной таблицей, найти функцию F определенного вида так, чтобы сумма квадратов Ф была наименьшей.
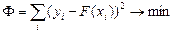 |
 Рассмотрим метод нахождения приближающей функции в общем виде на примере аппроксимирующей функции с тремя параметрами:
Рассмотрим метод нахождения приближающей функции в общем виде на примере аппроксимирующей функции с тремя параметрами: |
|
|
(1)
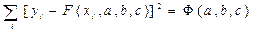 Пусть F(xi, a, b, c) = yi, i=1, 2, ..., n. Сумма квадратов разностей соответствующих значений f и F будет иметь вид:
Пусть F(xi, a, b, c) = yi, i=1, 2, ..., n. Сумма квадратов разностей соответствующих значений f и F будет иметь вид:
(2)
Эта сумма является функцией Ф(а, b, c) трех переменных (параметров a, b и c). Задача сводится к отысканию ее минимума. Используем необходимое условие экстремума:
 |
 Получаем систему для определения неизвестных параметров a, b, c.
Получаем систему для определения неизвестных параметров a, b, c.
 |
(3)
Решив эту систему получим конкретный вид искомой функции F(x, a, b, c). Как видно из рассмотренного примера, изменение количества параметров не приведет к искажению сущности самого подхода, а выразится лишь в изменении количества уравнений в системе (3).
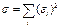 Значения найденной функции F(x, a, b, c) в точках х1, x2, ..., xn, будут отличаться от табличных значений y1, y2, ..., yn. Значения разностей yi-F(xi, a, b, c)=ei (i=1, 2, ..., n) называются отклонениями измеренных значений y от вычисленных по формуле (1). Для найденной эмпирической формулы y=F(x) в соответствии с исходной таблицей можно, следовательно найти сумму квадратов отклонений, которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции (и найденных значений параметров) должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя методу наименьших квадратов, лучшим нужно считать то, для которого сумма (2) имеет наименьшее значение.
Значения найденной функции F(x, a, b, c) в точках х1, x2, ..., xn, будут отличаться от табличных значений y1, y2, ..., yn. Значения разностей yi-F(xi, a, b, c)=ei (i=1, 2, ..., n) называются отклонениями измеренных значений y от вычисленных по формуле (1). Для найденной эмпирической формулы y=F(x) в соответствии с исходной таблицей можно, следовательно найти сумму квадратов отклонений, которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции (и найденных значений параметров) должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя методу наименьших квадратов, лучшим нужно считать то, для которого сумма (2) имеет наименьшее значение.
4. Точечная аппроксимация. Аппроксимация, при которой приближение строится на заданном дискретном множестве точек  , называется точечной.
, называется точечной.
Для получения точечного среднеквадратичного приближения функции  , заданной таблично, аппроксимирующую функцию
, заданной таблично, аппроксимирующую функцию  строят из условия минимума величины
строят из условия минимума величины
 ,
,
где 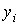 – значения функции
– значения функции 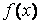 в точках
в точках 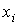 .
.
Основная сфера применения среднеквадратичного приближения – обработка экспериментальных данных (построение эмпирических формул).
Другим видом точечной аппроксимации является интерполирование, при котором аппроксимирующая функция принимает в заданных точках 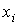 , те же значения
, те же значения 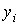 , что и функция
, что и функция 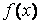 , т. е.
, т. е.

 ,
, 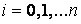 .
.
В этом случае, близость интерполирующей функции к заданной функции состоит в том, что их значения совпадают на заданной системе точек.
|
|
|
На рис. 4. 1. показаны качественные графики интерполяционной функции (сплошная линия) и результаты среднеквадратичного приближения (пунктирная линия). Точками отмечены табличные значения функции 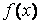 .
.
Невязка – разница между эмпирическими значениями и значениями аппроксимирующих линий; или разница между наблюденными аппроксимирующих функций.
Поиск простейших эмпирических зависимостей необходим чтобы упорядочить значения системы, заменить одну систему координат на другую.
Z = axm
lnz = lna + m lnx соответственно Y = AX + B – линейная зависимость, а х = lnx и у = lnz – логарифмич замена. Переходим к билогарифмированию:

В естествознании часто используется метод наименьших квадратов - метод оценивания параметров приближающей функции, кот сводит к min сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции.
|
|
|


