Цель работы. Освоепис графических методов развертывания поверхностей.

2. Задание. Ознакомиться с масштабным плазом и провести развертывание по­верхности.

Основные сведения.

Метод универсален, но его применение целесообразно, когда нормаль к сред­нему шпангоуту не является таковой к остальным, а прогрессы по нормали перемен­ны.

При этом методе в качестве строевой для развертки листа используется геоде- _ зическая линия.

Два определения геодезической линии:

- геодезической линией какой-либо поверхности называется линия, в любой точке которой ее соприкасающаяся плоскость и плоскость, касательная к поверхности, взаимно перпендикулярны;

- геодезической линией какой-либо поверхности называется линия, в любой точке которой ее главная нормаль совпадает с нормалью к поверхности.

Геодезическая линия соединяет точки поверхности по наикратчайшему рас­стоянию.

Применение геодезической линии поверхности листа в качестве строевой при развертке основано наследующем:

- при спрямлении развертываемых поверхностей на плоскость их геодезические липни становятся прямыми;

- при спрямлении па плоскость узкой полосы, вырезанной из любой поверхности вдоль геодезической линии, полоса становится плоской и прямой.

Построение геодезической линии на проекции «корпус» плазового чертежа производится следующим образом.

14

Концы отрезка среднего или ближайшего к середине листа шпангоута, прини­маемого за начальный шпангоут, соединяют хордой, а затем проводят касательную к этому шпангоуту, параллельную хорде (рис. 4а).

Находят точку сопряжения касательной со шпангоутом. Для этого на касатель­ной отмечают две точки, одинаково удаленные (например, на расстояние у) от дуги шпангоута, а затем делят отрезок касательной между этими точками пополам. Сере­дина отрезка (точка 0 на рис. 4а) и есть искомая точка.

В точке 0 восстанавливают перпендикуляр к касательной (нормаль к начально­му шпангоуту) и прочерчивают его через всю проекцию листа (А|Ац на рис. 4а). За­тем определяют отклонение Л, проекции геодезической линии от прямой АО на каж­дом шпангоуте.

Приближенная расчетная формула имеет вид:

f=«

где i - условные порядковые номера шпангоутов, расположенных в нос и в корму от шпангоута, принятого за начальный, номер которого принимается равным нулю (на рис.4а ц = 0), номера i = 2,3 и т.д. имеют по два шпангоута - по одному с носо­вой и с кормовой стороны (на проекции «корпус» плазового чертежа - по одному слева и справа от начального шпангоута (нарис. 4а i₅ = i₇= I, i₄ = i_s = 2 и т.д);

n -условный порядковый номер того шпангоута, на котором определяется от­клонение Д проекции геодезической линии от прямой;

ДЬ - расстояние между соседними шпангоутами (i-м и (i-l)-M и (i-2)-M н т.д.), замеренное вдоль нормали к начальному шпангоуту (на рис. 4а - вдоль линии А|Ац) на проекции «корпус» плазового чертежа (так называемый «прогресс» шпангоутов в пределах одной шпации), мм;

Ф - угол между нормалью к начальному шпангоуту и нормалью к рассматривае­мому шпангоуту (i-ну, (i- l)- ny и т.д.), восстановленной из точки пересечения этого шпангоута с нормалью к начальному шпангоуту, рад.

В качестве примера запишем расчетную формулу для определения Д на второй шпангоуте листа. Условный порядковый номер этого шпангоута относительно на­чального - i=4 а, следовательно, формула приобретает вид:

Д 4 = (AKj.j- АЬз _2)-фз + 2(ДЬз _2 - ЛЬг -О -срг ⁺ 3(Ab ₂.i - At>i_o)-(pi.

Вычисление значений Д удобно представлять в виде таблицы (пример - для листа, изображенного на рис. 4а) (табл.1).

15

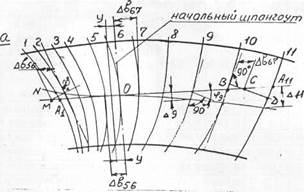
Рис. 4. Развертывание поверхности методом Геодезических линий

 

 

Таблица ^т

Вычисление значений Л в табличной форме

Но

Мер

шп

Ан-

Го-

Ута