Влияние дисконтной ставки на ранжирование проектов по критерию NPV

 

Рис. 7.1 показывает, что с ростом k графики NPV проектов 5 и L убывают. Заметим, что проект L имеет более высокое значение NPV при низких значениях k; при k > 7.2% уже проект S имеет более высокие значения NPV. Заметим также, что NPV_L «более чувствителен» к изменению дисконтной ставки, чем NPV_S, поскольку с ростом k NPV_L убывает более высокими темпами.

Чтобы понять, почему проект L более чувствителен, вспомним, что приток денежных средств в проекте S идет более быстрыми темпами, т. е., как было определено выше, S — краткосрочный проект, a L — долгосрочный проект. Рассмотрим уравнение для NPV:

Теперь отметим, что знаменатели слагаемых в этой формуле увеличиваются с ростом k и t и это увеличение идет по экспоненте; следовательно, эффект роста k более ощутим, если значение t больше. Понять это достаточно просто, обратившись к следующим данным:

PV 100 дол. притока денежных средств за первый год, дисконтиро­ванного по ставке 5%................................................……………………………………………………………	95.24 дол.
PV 100 дол. притока денежных средств за первый год, дисконтиро­ванного по ставке 10%..............................................…………………………………………………………..	90.91 дол.
Темп снижения PV в результате увеличения k на 5 процентных пунктов при t = 1.…	-4.5%
PV 100 дол. притока денежных средств за десятый год, дисконтирован­ного по ставке 5%...................................................…………………………………………………	61.39 дол.
PV 100 дол. притока денежных средств за десятый год, дисконтирован­ного по ставке 10%..................................................………………………………………………..	38.55 дол.
Темп снижения PV в результате увеличения k на S процентных пунктов при t =10....	-37.2%

Увеличение дисконтной ставки на 5% является основанием для снижения PV при t = 1 только на 4.5%, но такое же увеличение ставки при t = 10 снижает PV на 37.2%. Таким образом, если проект имеет большую часть поступлений в начальные годы, его NPV с ростом k будет убывать значительно медленнее по сравнению с проектом, в котором в первые годы поступает относительно мень­шая часть общего притока денежных средств.

Следовательно, проект L, который имеет большую часть поступлений в по­следние годы, очень невыгоден, если дисконтная ставка повышается, тогда как проект S, в котором приток денежных средств идет более быстрыми темпами в первые годы, в меньшей степени реагирует на увеличение ставки.

 

Независимые проекты

 

Если два проекта независимы, тогда критерии NPV и IRR дают одинаковый результат в отношении принятия или отклонения проекта: проект, принятый по критерию NPV, будет принят и по критерию IRR, и наоборот. Чтобы понять это, вернемся к рис. 7.1 и заметим, что: 1) проект принимается, если цена капитала меньше IRR, и 2) NPV проекта всегда положителен при цене капитала меньше IRR. Таким образом, для всех значений цены капитала, меньших 11.8%, проект L будет принят по обоим критериям, тогда как оба критерия признают проект негодным, если цена капитала выше 11.8%. Проект S, как и все другие независимые проекты, может быть проанализирован аналогично, при этом всегда будет соблюдаться условие: если IRR > k, то NPV > 0.

 

Альтернативные проекты

 

Теперь предположим, что проекты S и L альтернативные, т. е. не являются независимыми. Это означает, что можно выбрать либо проект S, либо проект L, либо оба проекта отвергаются, но нельзя принять оба проекта одновременно. Из рис. 7.1 видно, что при k > 7.2%, NPV_S > NPV_L и IRR_S > IRR_L. Таким образом, при k > 7.2% оба критерия дают одинаковый результат при выборе проекта из двух альтернативных. При k < 7.2% критерии дают уже различные результаты: по критерию NPV предпочтителен проект L, по критерию IRR — проект S. Какой же ответ будет правильным? Логика подсказывает, что критерий NPV лучше, так как он выбирает тот проект, который увеличивает благосостояние акционеров в большей степени.10

Причины, приводящие к противоречию. Две основные причины обусловливают пересечение графиков NPV и тем самым приводят к противоречию критериев NPV и IRR: 1) масштаб проекта, т. е. величина инвестиций по одному проекту больше, чем по другому; 2) интенсивность притока денежных средств, т. е. большая часть притока денежных средств по одному проекту осуществляется в первые годы, по второму — в последние, что и имело место с проектами L и S.11

Если подобные различия появляются при анализе проектов, фирма будет иметь неодинаковые объемы свободных ресурсов для инвестирования в различные годы в зависимости от того, какой проект был выбран ею. Например, если один проект требует большего инвестирования, чем второй, тогда, выбрав второй проект, фирма в момент t = 0 будет иметь свободные финансовые ресурсы, доступные для инвестирования в какой-то дополнительный проект. Аналогично, если проекты требуют одинаковых инвестиций, но приток денежных средств по одному из них осуществляется быстрее, фирма получит дополнительные воз­можности для их рефинансирования. В подобной ситуации очень важное значе­ние имеет цена капитала, при которой приростные денежные поступления могут быть реинвестированы. Это положение проиллюстрировано ниже.

1. Масштаб проекта. Альтернативные проекты очень часто различаются по величине. Предположим, фирма имеет возможность купить рудник по добыче меди за 5 млн. дол. Если покупка состоится, компания сможет транспортиро­вать руду для переплавки двумя способами. План S (небольшой проект) пре­дусматривает покупку парка грузовых автомобилей за 1 млн. дол., в результате стоимость проекта составит 6 млн. дол. План L (крупный проект) предусматри­вает затраты в 15 млн. дол. на установку конвейера для перемещения руды, что увеличит стоимость проекта до 20 млн. дол. Если использовать грузовики, то­гда затраты по их эксплуатации будут выше, чем при использовании конвейера. Для простоты предположим, что проект будет действовать в течение 5 лет, после чего запасы руды иссякнут. Допустим также, что ожидаемые посленалоговые денежные поступления имеют место в конце каждого года и составят 2 млн. дол. по плану 5 и 6 млн. дол. по плану L.

Считая цену капитала равной 10%, можно найти для каждого проекта NPV (в млн. дол.) и IRR:

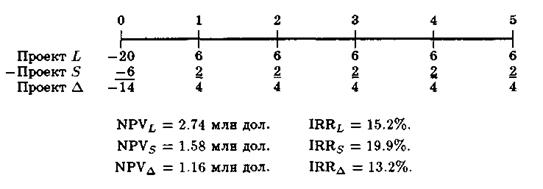
Таким образом, критерии приводят к разным результатам: NPV_L > NPV_S, но IRR_S > IRR_L. Какой же проект следует принять? Если предположить, что цена капитала постоянна, т. е. фирма может привлекать средства в требуемых объемах на условии 10%, тогда следует выбрать проект с большим NPV, т. е. L. Можно рассмотреть еще один проект Δ как самостоятельный, составлен­ный из приростных значений исходных проектов и требующий инвестиций в 14 млн. дол. Следовательно, проект L может быть разбит на две составляю­щие: одна эквивалентна проекту S, а другая представляет собой «остаточный проект», равный гипотетическому проекту Δ. Для проекта Δ требуются ин­вестиции в размере 14 млн. дол., ежегодные поступления равны 4 млн. дол., а NPV равен разности между NPV_S и NPV_L, т. е. 1.16 млн. дол. Таким обра­зом, гипотетический проект Δ имеет NPV_Δ > 0, поэтому его следует принять. Следовательно, нужно принять проект L.

Можно привести другие рассуждения. Проект L может быть условно разде­лен на два проекта, первый с инвестицией 6 млн. дол. и NPV = 1.58 млн. дол. и второй с инвестицией 14 млн. дол. и NPV =1.16 млн. дол. Поскольку обе составляющие имеют NPV > 0, их следует принять. Если же проект S будет принят, вторая составляющая проекта L, т. е. гипотетический проект Δ, будет автоматически отвергнут. Таким образом, критерий NPV предпочтительнее, поскольку именно он не отвергает проект L.12

Значение k, при котором NPV проектов одинаковы, представляет собой IRR проекта Δ и равно 13.2%. При k > 13.2% противоречия между критериями NPV и IRR не возникает. В нашем примере k = 10%, что и привело к появлению конфликта.13

2. Интенсивность притока денежных средств. Противоречие между NPV и IRR может также возникать из-за различий в распределении общей суммы притока денежных средств во времени, даже если два проекта имеют абсолютно одинаковую величину исходных инвестиций. О возможности такого противоречия говорилось выше, при обсуждении критериев оценки. Рассмотрим еще один пример. Предположим, что анализируется проект о приобретении за 10 млн. дол. права на вырубку леса и изготовление пиломатериалов. Если мы немедленно начнем вырубку леса в соответствии с краткосрочным планом S, наши ожидаемые денежные поступления составят в первые два года по 4 млн. дол., в следующие два года по 3 млн. дол., в последние два года по 2 млн. дол. Имеется и другой план — долгосрочный план L, в соответствии с которым начало вырубки леса откладывается на год, что позволит деревьям подрасти. Благодаря этому приток денежных средств составит во втором году 2 млн. дол., в третьем 3 млн., в четвертом 5 млн., в пятом — 9 млн. дол.

Полагая, что цена капитала в каждом случае равна 10%, найдем NPV (в млн. дол.) и IRR для каждого проекта:

Вновь два критерия дают разные результаты: из-за различия в интенсивно­сти притока денежных средств NPV_L > NPV_S, но IRR_S > IRR_L.

Мы уже знаем, что высокая ставка дисконта оказывает большее влияние на элементы денежного потока последних лет. Поэтому график NPV долгосрочных проектов, таких как проект L, имеет большую крутизну наклона к оси абсцисс по сравнению с краткосрочными проектами типа проекта S. Если значение цены капитала лежит слева от абсциссы точки пересечения двух графиков, возникает противоречие. Именно эта ситуация и имеет место в нашем примере: цена капитала k = 10%, а абсцисса точки пересечения графиков 12.5%.

В предыдущем примере, когда два проекта различались по масштабу, но не имели различий в интенсивности притока денежных средств, мы подобрали гипотетический проект Δ, который имел положительный NPV, чтобы пока­зать, почему проект с большим NPV должен быть принят. Можно сделать аналогичные расчеты и для последнего примера. Проект L состоит из двух ча­стей: аналога проекта S и гипотетического проекта Δ с положительным NPV = 0.42 млн. дол. Принимая проект S, мы автоматически отвергаем проект Δ, т. е. теряем возможность увеличить стоимость фирмы. Таким образом, целесо­образно отвергнуть проект S и принять проект L.

Ключевой вопрос конфликта. Можно заметить, что в обоих рассмотренных примерах возникают приростные денежные потоки. Поэтому ключевым мо­ментом в анализе альтернативных проектов является решение вопроса о том, какова ценность ускорения притока денежных средств. Ценность денежного по­тока зависит от допустимой доходности, под которую можно реинвестировать приростные денежные поступления ранних лет. Использование критерия NPV безоговорочно предполагает, что доступной процентной ставкой, по кото­рой могут быть реинвестированы поступающие денежные средства, является цена капитала, тогда как применение критерия IRR означает, что у фирмы имеются какие-то инвестиционные возможности со ставкой, равной IRR. Эти предпосылки молчаливо предполагаются в процессе дисконтирования. Таким образом, по критерию NPV дисконтирование выполняется по цене капитала, тогда как по критерию IRR — по величине IRR проекта. Естественно, поступа­ющие денежные средства могут быть выплачены акционерам в виде дивидендов и потрачены ими на пиво и пиццу, тем не менее предпосылка о возможности реинвестирования является составной частью расчета критериев IRR и NPV.

Решение конфликта. Какая же из предпосылок обоснованнее: реинвестиро­вание генерируемых проектом денежных средств по цене капитала или реинве­стирование по ставке IRR проекта? Наша точка зрения такова.

1. Предположим, что цена капитала фирмы 10%. Руководство может при­влечь финансовые ресурсы в требуемых объемах по этой ставке. Данное условие предполагается неизменным на некоторое обозримое будущее. Далее допустим, что все потенциальные проекты имеют такую же степень риска, как и текущие проекты фирмы.

2. Процесс формирования бюджета капиталовложений предполагает, что по­тенциальные проекты должны быть оценены по ставке k = 10%. Все проекты с NPV > 0 принимаются. Необходимый для их финансирования капитал доступен как в настоящее время, так и в будущем.

3. Что же делать с поступающими денежными средствами, генерируемыми действующими проектами? Эти денежные средства могут быть: а) выплачены владельцам источников средств, т. е. акционерам и кредиторам, обеспечив им доходность в среднем 10%, или б) использованы в качестве альтернативы внешним источникам средств, цена которых равна 10%. Таким образом, фирма получит экономию в размере 10%, и эти 10% как раз и представляют собой допустимую и возможную ставку реинвестирования поступающих денежных средств.

4. Критерий IRB безоговорочно предполагает реинвестирование по самой ставке IRR. Также предполагается: а) доступность источников на рынке капитала и б) неизменность ожидаемой цены капитала, т. е. доступная ставка реинвестирования равна 10%. Даже если фирма принимает проекты с более высоким в среднем значением IRR, скажем 30%, это к делу не относится, так как новые проекты всегда могут быть профинансированы из внешних источников с ценой капитала 10%, поэтому доступная ставка реинвестирования денежных средств, генерируемых действующими проектами, опять же равна цене капитала фирмы.

Таким образом, мы пришли к заключению, что доступной и возможной ставкой реинвестирования является цена капитала, которая и подразумева­ется в критерии NPV. Этим обосновывается предпочтительность критерия NPV по крайней мере для фирм, имеющих желание и возможности привлекать капитал по разумной цене, близкой по значению и сложившейся в фирме цене капитала. В главе 10 при обсуждении проблемы оптимизации бюджета капиталовложений мы увидим, что при определенных условиях применение критерия NPV сомнительно, однако в большинстве случаев этот критерий несомненно лучше, чем IRR.

Еще раз повторим, что для независимых проектов оба критерия дают одинаковые результаты. Однако когда оцениваются альтернативные проекты, особенно различающиеся по масштабу и/или временной интенсивности притока денежных средств, должен применяться критерий NPV.

Множественность IRR

Другая ситуация, в которой критерий IRR не может быть использован, — это анализ неординарных проектов. В ординарном (normal) инвестиционном проекте один или несколько оттоков сменяются серией поступлений денежных средств; если же в проекте предполагается значительный отток денежных средств в ходе его реализации или по окончании, этот проект называется неординарным (nonnormal). Наиболее распространенная проблема при анализе неординарного проекта — это множественность IRR.

Уравнение (7.2) может иметь более чем одно решение, что и означает множественность IRR. Заметим, что это уравнение — многочлен n-й степени, поэтому оно имеет n различных корней. Для ординарного проекта все корни уравнения (7.2), за исключением одного, мнимые, поэтому и находится единственное значение IRR. В случае с неординарным проектом число действительных корней больше единицы, что и приводит к множественности значений IRR.

Чтобы проиллюстрировать эту проблему, представим фирму, вкладывающую 1.6 млн. дол. в добычу ископаемых (проект М). В течение первого года рудник дает доход 10 млн. дол., тогда как в течение второго года необходимо будет провести работы по восстановлению окружающей среды на сумму 10 млн. дол. Таким образом, ожидаемый денежный поток имеет вид (в млн. дол.):

Получим два решения: NPV = 0 при IRR = 25% и IRR = 400%.14 Эта ситуация показана на рис. 7.2.15 Заметим, что проблемы не возникает, если применяется критерий NPV. Так, если цена капитала проекта М равна 10%, то его NPV = - 0.77 млн. дол. и проект должен быть отвергнут; если k находится в интервале между 25 и 400%, то NPV > 0.

Авторам известен подобный пример из практики с множественностью IRR, когда главный банк Калифорнии получил заем у страховой компании и исполь­зовал эти средства вместе с собственным капиталом для покупки реактивных двигателей, которые затем были сданы в аренду одной из крупных авиакомпаний. Банк ожидал получить в первые годы приток денежных средств (арендные платежи плюс налоговые льготы минус ссудный процент страховой компании), затем несколько достаточно значительных оттоков, связанных с погашением долга страховой компании, и, наконец, большой приток от продажи двигателей по окончании срока аренды.16

В ходе анализа были получены два значения IRR, поэтому возник вопрос, какой из них корректен. Нельзя было игнорировать критерий IRR и ограничиться расчетом NPV, так как аренда была уже оформлена и руководство банка, а также наблюдатели Федерального резервного банка хотели знать эффективность операции. Нас попросили помочь решить эту проблему, и мы посоветовали банку пересчитать притоки и оттоки по данному проекту, нарастив их по ставке реинвестирования в 9%, численно равной проценту по предоставляемым банком ссудам. Для пересчитанного денежного потока была рассчитана IRR, которая и была охарактеризована как доходность от аренды. Эта процедура, которая по сути представляет собой расчет модифицированной IRR и будет обсуждена в следующем разделе, удовлетворила все заинтересованные стороны.

Только что рассмотренные примеры высветили лишь одну из проблем, связанных с использованием критерия IRR, — проблему множественности значений IRR для неординарных денежных потоков. Могут возникать и другие вопросы при анализе подобных потоков, как-то: отсутствие IRR или нахождение такого ее значения, которое может привести к неверным решениям в оценке приемлемости проектов. Во всех таких случаях куда проще использовать критерий NPV, и он в концептуальном плане приводит к правильным решениям в области инвестиционной политики.

 

Вопросы для самопроверки

Опишите, как построить график NPV.

Что характеризует точка пересечения графиков NPV и как она влияет на выбор альтернативных проектов?

Какие две основные причины приводят к противоречиям между критериями IRR и NPV?

Какая ключевая предпосылка приводит к противоречию между IRR и NPV? Если конфликт существует, какой критерий — IRR или NPV — предпочтителен и почему?

Объясните разницу между ординарным и неординарным проектами.

В чем заключается проблема множественности IRR и когда она возникает?

Модифицированная внутренняя доходность

 

Не смотря на приверженность ученых критерию NPV, исследования показывают, что практические работники предпочитают критерий IRR критерию NPV в соотношении 1: 3. Возможно, менеджерам более привлекателен анализ инвестиций в терминах относительных, а не абсолютных величин. Имея это в виду, зададимся вопросом, нельзя ли построить относительный показатель эффективности взамен обычной IRR? Ответ – да, можно модифицировать IRR и сделать ее показателем эффективности, пригодным для использования при построении бюджета капиталовложений. Этот показатель, называемый модифицированной IRR (Modified IRR, MIRR), определяется следующим образом:

PV инвестиций = PV TV,

(7.2a)

Здесь COF означает оттоки денежных средств, или инвестиций, a CIF — при­токи. В левой части формулы — дисконтированная по цене капитала величина всех инвестиций, числитель в правой части — это наращенная стоимость денеж­ных поступлений при предположении, что они могут быть реинвестированы по цене капитала. Этот показатель называется терминальной стоимостью (Ter­minal Value, TV). Ставка дисконта, уравнивающая PV инвестиций и TV, опре­деляется как MIRR.17

Если все инвестиции имеют место при t = 0, а первый приток происходит при t = 1, что и имеет место в наших проектах S и L из табл. 7.1, тогда эта формула принимает следующий вид:

величина инвестиции = (7.26)

Логику расчета по этой формуле для проекта S можно представить в виде схемы:

Расчеты по этой формуле для проектов L и S дают следующие результаты: MIRR_S = 12.1%, MIRR_L = 11.3%.

Показатель MIRR имеет существенные преимущества перед обычной IRR. MIRR предполагает, что все денежные поступления по проекту реинвестируются по цене капитала, тогда как IRR предполагает, что реинвестирование происходит по цене источника данного проекта. Поскольку реинвестирование по k в целом более корректно, MIRR в лучшей степени отражает доходность проекта. MIRR также решает проблему множественности IRR. В частности, в задаче о добыче ископаемых (проект М): при k = 10% имеем MIRR = 5.6%, т. е. проект должен быть отвергнут. Это соответствует заключению по критерию NPV, так как NPV = -770000 дол.

Можно ли использовать MIRR, так же как NPV, для выбора альтернативных проектов? Если два проекта равны по масштабу и продолжительности, то NPV и MIRR дают одинаковый ответ. Таким образом, для всех проектов типа S и L, если NPV_S > NPV_L, то MIRRS > MIRRL, и никаких противоречий, как это было при сравнении NPV и IRR, не возникает. Если проекты одинаковы по масштабу и различны по продолжительности, MIRR и NPV приведут к одинаковому результату при условии, что MIRR рассчитана исходя из продолжительности долгосрочного проекта (в этом случае для краткосрочного проекта недостающие денежные поступления берутся нулевыми). Однако если альтернативные проекты существенно различаются по масштабу, можно прийти к противоречивым оценкам, т. е., сравнивая большой (L) и маленький (S) проекты, можно получить: NPV_L > NPV_S, но MIRR_S > MIRR_L.

Мы полагаем, что MIRR предпочтительнее IRR в качестве характеристики реальной доходности проекта, или «ожидаемой долгосрочной нормы проекта», но NPV все-таки лучше для анализа альтернативных проектов, различающихся по масштабу, поскольку он показывает определенно, насколько оптимальный проект увеличивает стоимость фирмы.18

 

Вопросы для самопроверки

Кратко опишите алгоритм расчета MIRR.

В чем принципиальное различие между MIRR и IRR?

Какие преимущества имеет MIRR над IRR при разработке инвестированного бюджета?

При каких условиях может возникнуть противоречие между MIRR и NPV?

 

⇐ Предыдущая26272829303132333435Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: